葛劳渥方法及其局限性

葛劳渥（Glauert）方法是从风轮圆盘模型和叶素-动量定理演化而来，它考虑了尾流的旋转效应。葛劳渥方法的基本思路如下：

将图2-6a改画成图6-13的形式，比较两图，有

，此时，式（2-18）变成

dF=ρπrv²_∞（1-k²）dr （6-25）式（2-26）变成

dM=ρπv_∞Ωr³(1+k)(h-1)dr （6-26）

相应的式（2-31）可写成

dP=ΩdM=ρπv_∞Ω²r³(1+k)(h-1)dr （6-27）

从图6-13可得

式中 λ_r=Ωr/v∞。

由于升力和阻力为

可知

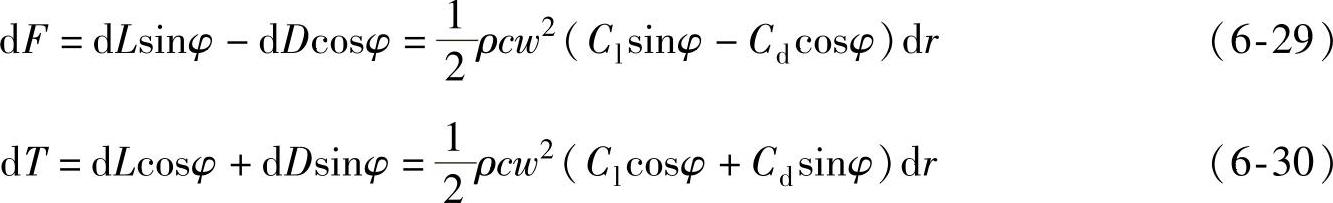
假设tanε=C_d/C_l，则有

那么，在叶片上的r～r+dr环域内，气流所产生的轴向推力为

式中 c——叶素弦长；

N——风轮叶片数。

图6-13 叶素受力图

气流所产生的转矩为

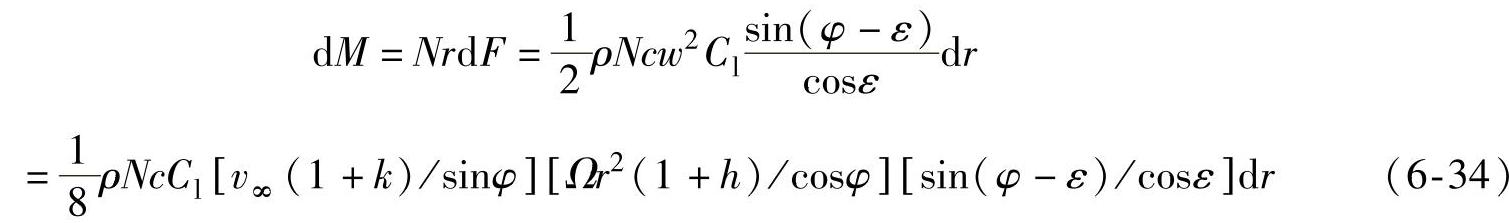
由式（6-25）和（6-33）可有

由式（6-26）和（6-34）得

以上两式又可写成

G=（1-k）/（1+k）=[C_lNccos（φ-ε）]/[8πrsin²φcosε] （6-37）

E=（h-1）/（h+1）=[C_lNcsin（φ-ε）]/[4πrcosεsin2φ] （6-38）

由以上两式可得

G/E=cot（φ-ε）cotφ（6-39）

与简化叶素-动量定理设计法相同，忽略阻力，即认为ε=0，并且应用式（6-28），

则有(www.xing528.com)

G/E=[（1-k）（h+1）]/[（1+k）（h-1）]=cot²φ=λ²_r[（h+1）/（1+k）]² （6-40）

从而得

由式（6-27），风能利用系数为

C_P=dP/ρπrv²_∞dr=λ²_r（1+k）（h-1） （6-43）

将式（6-42）代入式（6-43）则

从气动角度来看，最佳叶片应满足在叶片各处C_P都达到最大值，亦即对于给定的λ_r，使。

对C_P求导后可得

4k³-3k（λ²_r+1）+λ²_r+1=0 （6-45）

为了求解上式，可令

将其代入式（6-45），并将各项除以(λ²_r+1)3/2，得

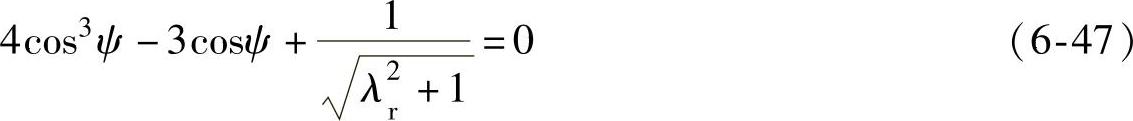
即

从而可解得

这样，对于理想风轮，若给定叶尖速比λ和攻角沿叶片径向的变化规律α_i=α（r_i），则可利用上面一些公式进行优化设计。具体步骤如下：

1）给出r_i，攻角α_i已知，C_l也已知；

2）求当地速度比λ_i，λ_i=λr_i/R；

3）由式（6-49）求出ψ_i；

4）由式（6-46）求出k_i；

5）由式（6-42）求出h_i；

6）由式（6-43）求出φ_i，

7）求叶素桨距角，β_i=φ_i-α_i；

8）叶素弦长，

表6-2给出不同当地速度比λ_i时，计算得到的参数设计结果。

表6-2 随λ_i变化的设计参数

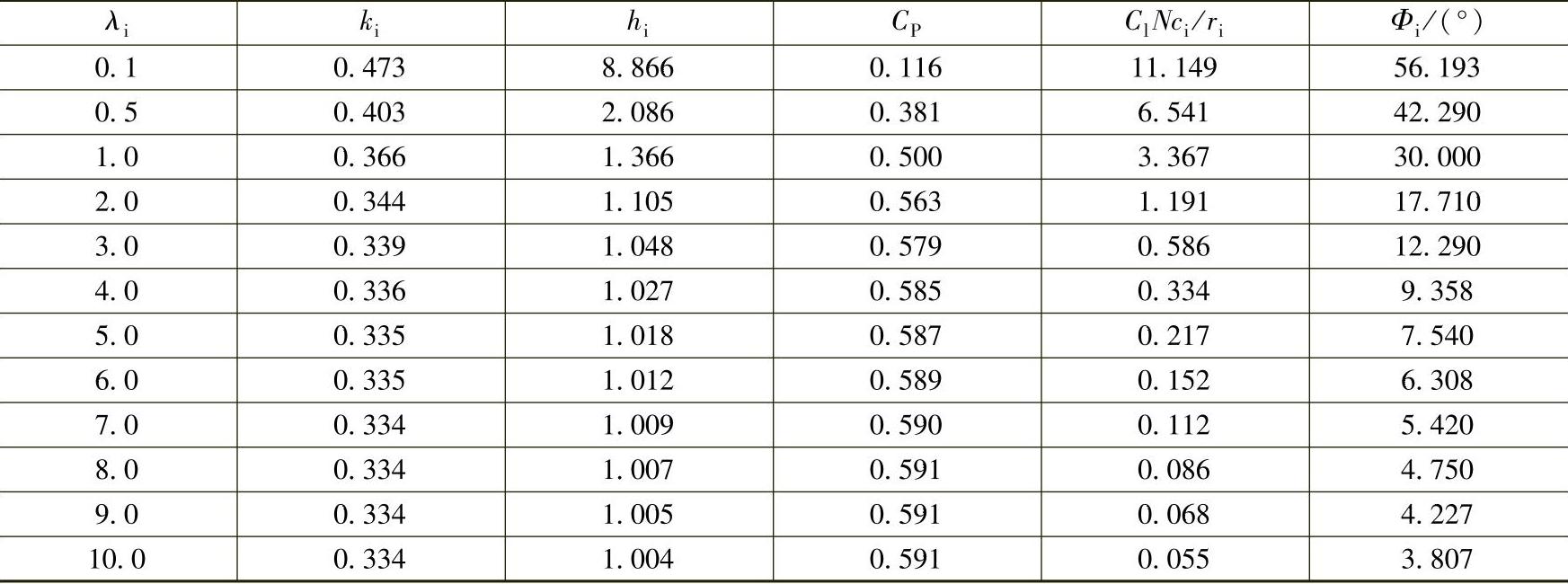
通过以上计算可得到沿叶片各径向位置r上的弦长c和叶素桨距角β，即可完成优化设计。葛劳渥方法是应用较广的方法之一。但要注意两点。一是对接近根部处的过大弦长和安装角要进行修正；二是对所设计的外形应计算其功率特性曲线，然后再根据结果对外形作必要的修正。

葛劳渥方法沿用诱导速度均匀的假设，忽略了叶尖损失和升阻比对叶片性能的影响，是产生设计误差的主要原因。