设计成本模型及其在风电行业中的应用

由式（5-8）可见，风轮的功率与风轮直径的平方成正比。而风轮质量与风轮直径的立方成正比。风轮直径越大，成本越高，但获得的能量越多。多大容量的风力发电机组其发电成本最少，这是个值得研究的问题。根据实践，可用一个成本模型来研究成本问题。

首先选一个风力发电机组作为基准，其各部件的成本是已知的，在结构相同的情况下，改变设计参数，则部件尺寸和质量发生变化。部件成本不会简单地与质量变化成正比，通常成本与质量的关系为

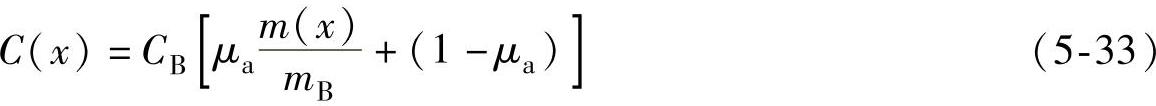
式中 C（x）——部件成本；

m（x）——部件质量；

x——设计参数；

C_B——成本的基准值；

m_B——质量的基准值；

μ_a——随质量变化的比例系数。

在产品开发的初期阶段，选择μ_a值具有一定局限性，应根据丰富的经验选择μ_a值，一般基于相似关系按比例得到，通常可取0.7～0.9。

【例5-5】 选用某风轮直径60m、1.5MW的风力发电机组作为基准机组，估计新开发机组成本，各部件成本占总成本的百分比可参照表5-1。

新开发风力发电机组的结构尺寸是根据基准机型将部件结构尺寸按相同比例缩放得到的（不包括齿轮箱、发电机、电网连接、控制器）。为保证在给定风速v下，叶尖速比λ值不变（λ=πDn/v），因为这时叶片空气动力性能良好，则风轮直径D和风轮转速n成反比例。遵守此反比例关系，则各机组的设计均可在相同额定风速下达到额定功率，因此额定功率正比于风轮直径的平方。

风轮转矩通过低速轴（主轴）传递给齿轮增速箱。齿轮箱根据风轮转矩M（N·m）设计，M=9550P/n，额定功率P的单位为kW，风轮转速n单位为r/min，由叶尖速比公式，当λ、v一定，则要求D·n=定值，故n与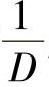成正比，所以风轮转矩M与风轮直径D的立方成正比。也就是主轴以及齿轮箱的质量均与风轮直径的立方成正比。那么，除了发电机、控制器和电网连接以外，风轮直径为D的风力机成本为(www.xing528.com)

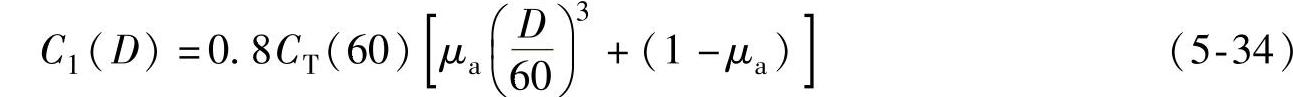
式中，C_T（60）——基准风力发电机组的总成本。

发电机是根据额定功率设计的，发电机的额定功率和电网连接均与风轮直径的平方成正比例。假设式（5-33）适合这些部件成本的计算，但质量比m（x）/m_B可用直径的平方比代换，则发电机和并网设备的成本为

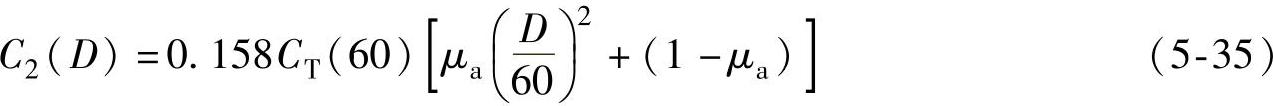
式（5-35）中的0.158是因发电机和并网成本占总成本的15.8％（见表5-1）。

假设控制器的成本仍占总成本的4.2％（见表5-1），则新的风力发电机组的总成本C_T（D）是新的风轮直径D的函数，即

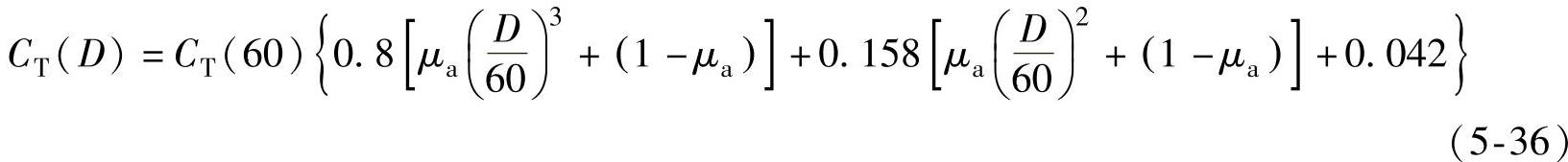
如果取D=90，μ_a=0.8，则有C_T（D）=2.678C_T（60）。

若不考虑机组运行和维护费用，电能成本可用上述的风力发电机组成本除以年发电量表示，即

Q=C_T(D)/E_y （5-37）

式中 Q——电能成本指数，单位为元/（kW·h/年）；

E_y——年发电量，单位为kW·h/年。