如何预测风力机的极限载荷？

风力机在进行抗极载荷破坏设计时，需要得出其极限载荷响应，此时的极限载荷分布很有意义。通常考虑如下载荷工况：

1）切出风速附近10min平均风速下的正常运行；

2）50年一遇10min平均风速下的停机状态；

3）保护系统故障、高风速下的故障运行。

对于上述载荷工况，假定通过气弹仿真得到n个10min时间序列载荷响应X。下面的量与从n个时间序列中得到的载荷响应X有关：

1）均值μ；

2）标准偏差σ；

3）偏斜度α₃；

4）峰度α₄；

5）均值μ上的比率ν_μ；

6）10min最大值x_m。

10min载荷响应X最大值X_m不是一个固定值，但有其固有的可变性，可以由一个概率分布来表示。这种固有的可变性用n个仿真时间序列的不同x_m值来反应。10min最大载荷响应的均值由μ_m表示，标准偏差由σ_m表示。对于设计而言，特征载荷响应通常取10min最大载荷响应分布的某个分位数。

有两种不同的基本方法来预测最大载荷响应及其分布的特定分位数：

1）统计模型：它利用了从以n个仿真最大值x_m表示的n个仿真时间序列得到的最大载荷响应的信息。

2）半解析模型：基于随机过程理论，它利用了以4个统计矩μ、σ、α₃和α₄以及交叉比率ν_μ表示的载荷响应过程的信息。

在随后的内容中将对两种方法及其精度水平进行讨论。

1.统计模型

10min最大载荷响应X_m可以假定趋近于冈贝尔分布，即

式中 α——尺度参数；

β——位置参数。

n个仿真时间序列有n个最大载荷响应观察值X_m。为了估计α和β，n个值X_m按照从小到大的顺序排列，即X_m，1，…，X_m，n。利用这些数据可以计算得到两个系数b₀和b₁，即

而α和β可以由下式估计：

式中 γ_E——欧拉常数，γ_E=0.57722。

X_m的平均值和标准偏差通过下式分别进行估计：

X_m分布的θ分位数通过下式进行估计：

式中

θ分位数估计的标准误差通过下式进行估计：

对于θ分位数由均值μ_m取代的特殊情况，上式简化为

假定θ分位数估计为正态分布，则其1-α置信度下θ分位数的双边置信区间变成(www.xing528.com)

式中 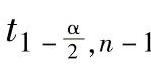——具有n-1个自由度的Student’s t分布的1-α/2分位数。

如果目的是得到指定置信度下的特征值，则通常取置信度的上限值，也就是说只考虑单边置信区间。带置信度1-α的特征参数变为

应该注意的是，为了获得足够精确的x_m，θ或_μm估计值，需要足够多的仿真次数n。

例如，考虑一个载荷响应过程X，它的10min极限值X_max根据n=5次的10min仿真时间序列进行估计。关于极值分布的估计如下：

求当分位数θ=95％时，即1-α=95％时的X_max估计。给定k_θ=1.866。95％分位数下X_max的中心估计值为

此估计下的标准误差为

Student’s t分布下的相关分位数t_1-α/2，n-1=2.78，x_m，95％的双边置信区间变成了4.673±2.78×0.413=4.673±1.148，这表示在中心估计值附近有很宽的区间。如果n由5次变为100次，则区间大大缩小为4.673±0.183。

2.半解析模型

半解析模型是由达文波特（1961）给出的，它利用了n个10min载荷响应时间序列更多的信息，而不仅仅是n个最大响应值x_m。载荷响应X可以看作10min序列的随机过程。过程X可以看作母标准高斯过程U的二次变换，即

X=ζ+η（U+εU²）ε＜＜1

下列表达式给出了系数的一阶近似：

其中用到了载荷响应过程X的均值_μ，标准差σ和偏斜度α₃。

X_m的均值和标准偏差的估计分别为

对应地，T表示持续时间，通常指仿真时间序列长度，也就是T=10min。对应地冈贝尔分布参数α和β的估计表示为

均值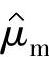的标准误差为

式中 n——样本尺寸，也就是上式中估计_μm的10min序列个数。

如果认为通过式（4-29）可以准确确定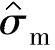，则1-α置信度下μ_m的双边置信区间为

式中 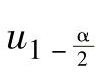——标准正态分布函数的1-α/2分位数。

3.两种模型的比较

半解析结果通常可以提供比统计结果更高精度的极值估计，这是因为半解析方法比统计方法利用了更多的信息。换句话说，为了获得同样精度的极值估计，半解析法比统计方法需要更小的采样尺寸n。因此建议，在预测极限载荷时，通常采用基于仿真载荷响应过程统计的半解析法，而不是仅仅采用最大观测值。

两个或更多随机选择的10min仿真时间序列可能给出十分不同的极限值。这就意味着如果只通过少数次仿真，选取平均极限载荷或最大载荷作为破断载荷，而不对极限载荷的统计特性进行恰当的考虑，将不会得到可重复的结果。进一步而言，该结果不能外推得到由分位数确定的特征值，也不能推广到持续时间不同于10min的载荷工况。半解析法考虑了极限载荷的随机特性，为通过载荷响应仿真时间序列对极限载荷进行分析提供了一种基本方法。

4.周期载荷的修正

前面介绍的半解析模型能够对不在运行状态的风力机的极限载荷提供十分准确的预测。对于运行状态下的载荷工况，必须考虑某些载荷其响应均值和标准偏差所具有的周期性。为此，可以采用一种基于方位“分仓（binning）”的方法。利用这种方法，风轮盘被划分为若干个扇区，每个扇区利用其方位角进行区分，当风轮盘被离散成m个等直径等角度的扇区时，载荷响应过程的扇区均值以及标准偏差就可以通过下面的式子建立：

式中 μ，σ——载荷响应X的平均值和标准偏差。

令α和β表示在时间历程T下正则化过程（X-μ）/α最大值的冈贝尔分布的分布参数，他们可以通过上述分析模型确定。时间历程T内所有扇区中X的最大极限值X_max的平均值μ_m的下限为

时间历程T内所有扇区中X的最大极限值X_max的平均值μ_m的上限为

关于此方法的详情参见Madsen等（1999）的相关研究。建议将风轮盘离散成m=36个扇区。