风况设计及安全规定：正常与极端风况

风力发电机组应设计成能安全承受对应安全等级的风况。设计文件应对设计风况进行详细规定。

从载荷和安全方面考虑，风况可分为正常风况和极端风况，正常风况指在风力机正常运行期间频繁出现的风况条件，而极端风况是指1年一遇或50年一遇的风况条件。

在多数情况下，风况条件是由稳定的平均气流与变化的可确定的阵风或湍流结合而成。在所有情况下，应考虑平均气流与水平面夹角达8°时的影响。假定这个气流倾斜角不随高度变化。

湍流是指风速矢量相对于10min平均值的随机变化。在使用湍流模型时应该考虑风速、风向和风切变变化的影响，并允许通过变化的风切变旋转采样（旋转采样是指对机组旋转风轮上某一固定点的风速矢量采样）。湍流风速矢量的三个分量定义如下：

——纵向：沿着平均风速方向；

——横向：水平并且与纵向垂直的方向；

——竖向：与纵向和横向均垂直的方向。

对于标准的风力发电机组等级，湍流模型中的随机风速场应该满足以下要求：

1）假定由后文给出的湍流标准偏差σ₁的取值不随高度变化。垂直于主风向的分量应该具备下述最小标准偏差：

——横向分量：σ₂≥0.7σ₁

——竖直分量：σ₃≥0.5σ₁

2）在轮毂高度z_hub处纵向湍流尺度参数Λ₁的值为

三个正交分量的功率谱密度S₁（f），S₂（f），S₃（f），随着惯性副区（风速湍流谱的频率区间，此区间内涡流经逐步破碎达到均匀化）内频率的增加，渐近于下式：

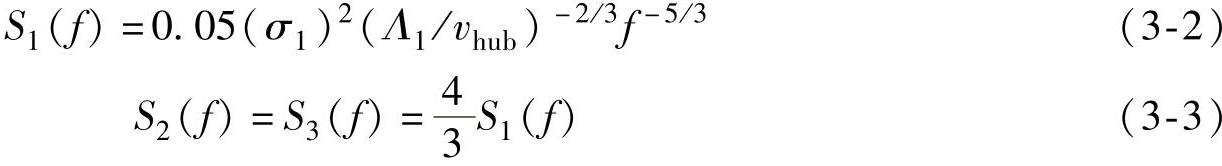
3）应该采用公认的相干模型。该模型定义为联合谱的幅值除以垂直于纵向的平面内、空间离散点上风速矢量纵向分量的自谱。IEC 61400-1-2005附件B推荐的曼恩（Mann）均匀切变湍流模型满足上述条件，同时还给出了另外一种满足上述条件的常用模型。其他模型要慎重使用，因为模型的选择会对载荷产生显著的影响。

1.正常风况

（1）风速分布 风速分布对于风力发电机组的设计有着很大影响，因为它决定着常规设计工况每种载荷状态的出现频率。应假设轮毂高度10min时间周期内平均风速符合下式描述的瑞利（Rayleigh）分布：

P_R（v_hub）=1-exp[-π（v_hub/2v_ave）²] （3-4）

式中 v_hub——轮毂高度处年平均风速，单位为m/s。

在标准风力发电机组等级中，v_ave应根据下式选取：

v_ave=0.2v_ref （3-5）

（2）正常风廓线模型（NWP）风廓线v（z）是地表以上平均风速对垂直高度z的函数。在标准风力发电机组等级下，正常风廓线由指数律公式给出：

v（z）=v_hub（z/z_hub）^α （3-6）

式中 z_hub——轮毂高度，单位为m。

假定指数α等于0.2。风廓线是用来确定风轮扫掠面垂直高度风切变的。

（3）正常湍流模型（NTM）对于正常湍流模型，纵向湍流标准差的典型值σ₁应以给定轮毂高度处风速的90％概率的标准差确定。

对于标准风力发电机组等级，此值由下式给定：

σ₁=I_ref（0.75v_hub+b）；b=5.6m/s （3-7）

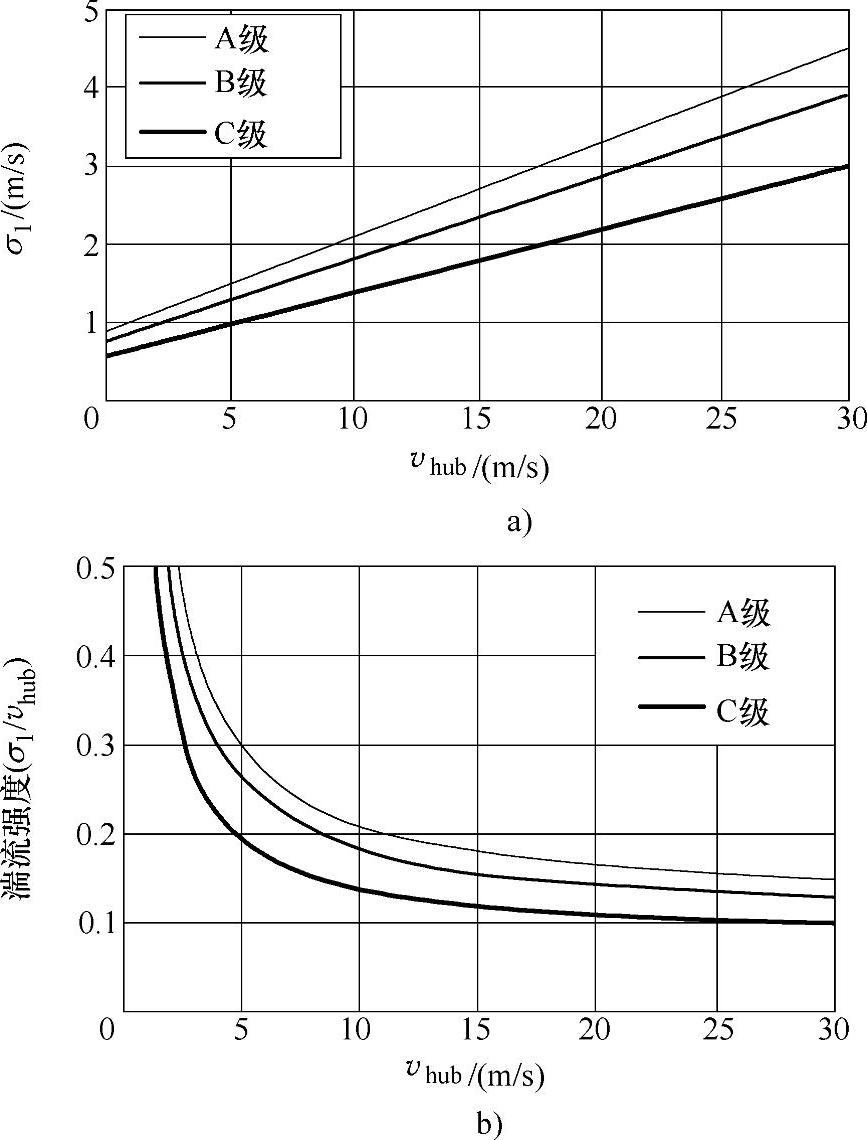
图3-1 正常湍流模型（NTM）

a）标准差与风速的关系 b）湍流强度与风速的关系

湍流标准差σ₁和湍流强度σ₁/v_hub如图3-1所示。I_ref的幅值在表3-1中给出。

2.极端风况

极端风况用于确定风力发电机组的极端风载荷，这些风况包括由暴风及风速和风向的迅速变化造成的风速峰值。

（1）极端风速模型（EWM）极端风速模型含稳态或湍流的风模型。风速模型应该基于参考风速v_ref和确定的湍流标准差σ₁。

对于稳态极端风速模型，50年一遇的极端风速v_e50和1年一遇的极端风速v_e1是高度z的函数，采用下面的公式计算：

在稳态极端风速模型中，一般假定与平均风向短期偏差为±15°。

对于湍流极端风速模型，50年和1年一遇情况下，10min平均风速为z的函数：

v_e50（z）=v_ref（z/z_hub）^0.11 （3-10）

v_e1（z）=0.8v_e50（z） （3-11）

纵向湍流标准差为

σ₁=0.11v_hub （3-12）

（2）极端运行阵风（EOG）对于标准风力发电机组等级，轮毂高度处阵风风速v_gust由下式给出：

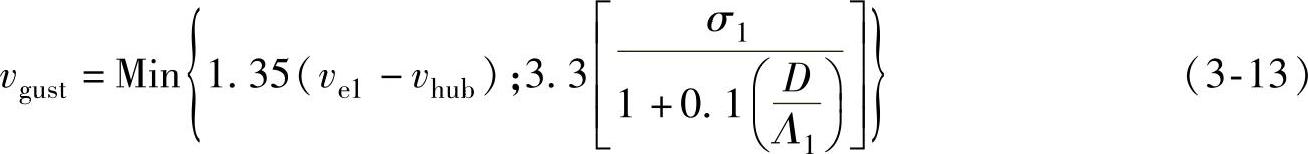
式中 σ₁——在式（3-7）中给出；

Λ₁——湍流尺度参数，见式（3-1）；

D——是风轮直径，单位为m。

风速由下式确定：

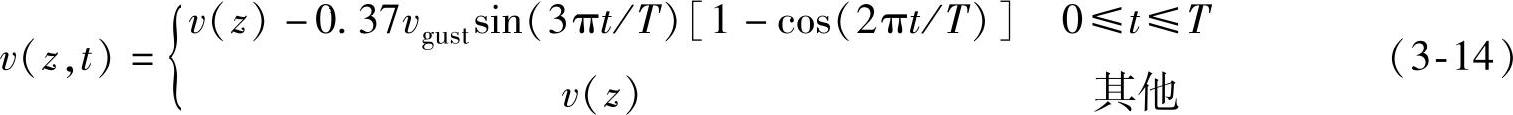
式中v（z）由式（3-6）确定，T为阵风持续时间，取T=10.5s。

【例3-1】 极端运行阵风实例：假设v_hub=25m/s，I_A级，D=42m。极端运行阵风如图3-2所示。(https://www.xing528.com)

（3）极端湍流模型（ETM）极端湍流模型采用正常风廓线模型（NWP）和下式给出的纵向分量标准差来确定。

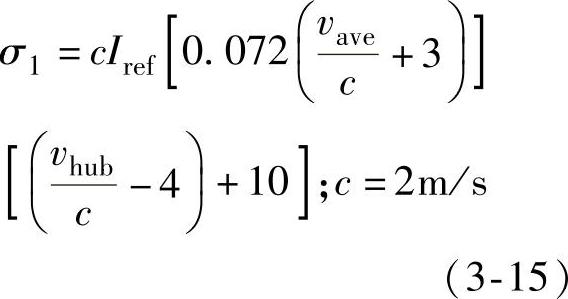
（4）极端风向变化（EDC）极端风向变化的幅值θ_e，由式（3-16）计算得出：

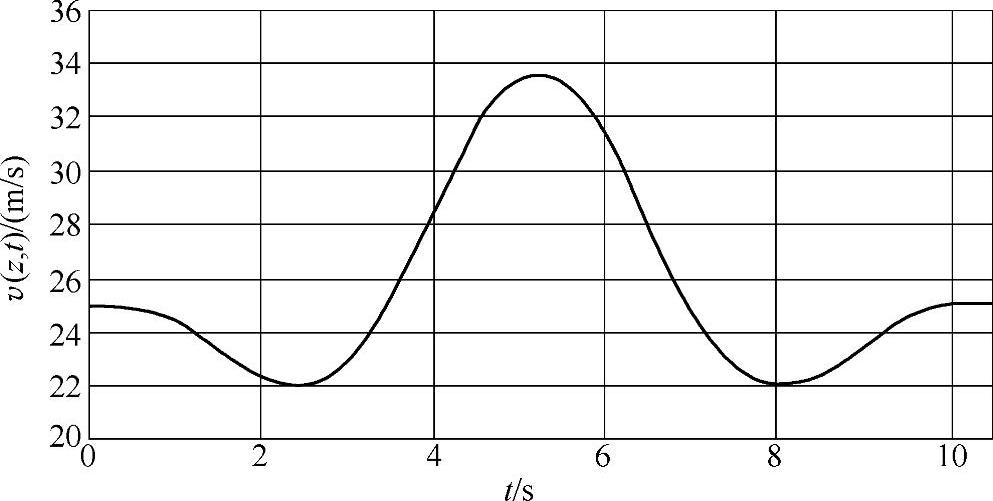
图3-2 极端运行阵风实例

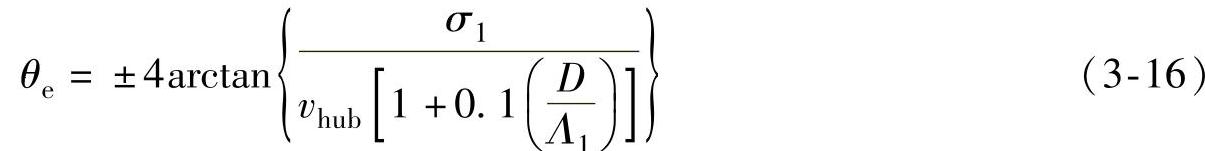
式中 σ₁——正常湍流模型（NTM）中的湍流标准差，见式（3-7）；

Λ₁——湍流尺度参数，单位为m，见式（3-1）；

D——风轮直径，单位为m。

θ_e取值范围为±180°。

极端风向变化瞬时值θ（t），由式（3-17）计算得出：

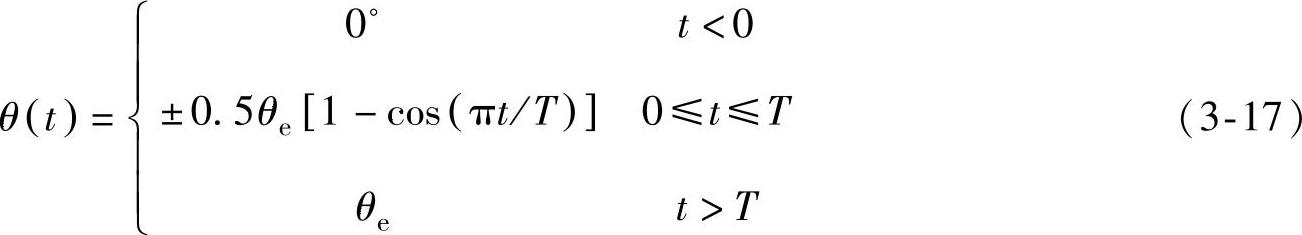
其中，T=6s是极端风向变化持续时间。符号的选择取决于最恶劣瞬时载荷发生情况。风向变化瞬态过程结束时，假定风向保持不变。风速应该按照正常风廓线模型（NWP）确定。

【例3-2】 极端风向变化实例：设D=42m，z_hub=30m，湍流类型A的极端风向变化幅值随轮毂风速v_hub变化的曲线如图3-3所示；图3-4所示为轮毂风速为v_hub=25m/s时对应的极端风向变化曲线。

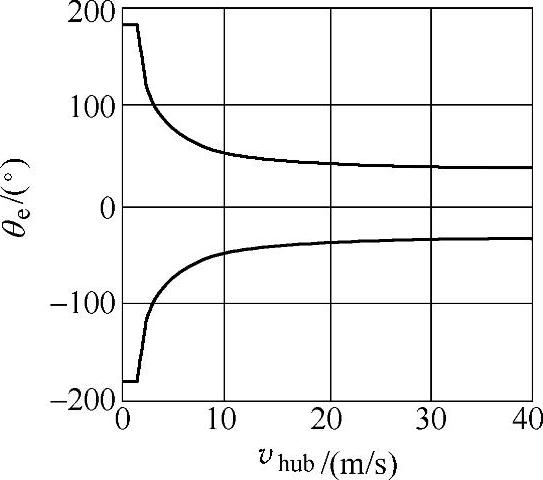
图3-3 极端风向幅值变化

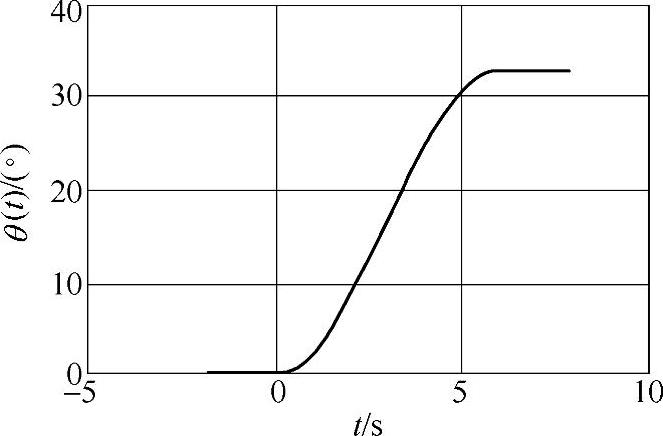
图3-4 极端风向变化

（5）方向改变的极端相关阵风（ECD）方向改变的极端相关阵风的幅值为

v_cg=15m/s （3-18）

风速定义式为

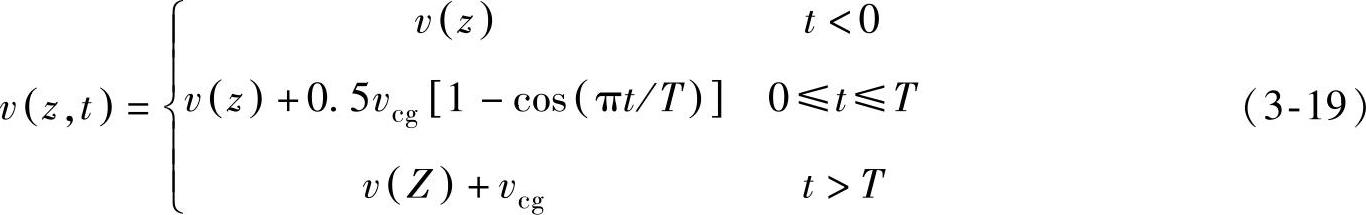
其中，T=10s为上升时间，风速v（z）由正常风廓线模型（NWP）给出。

【例3-3】 极端相关阵风期间风速的上升实例：设轮毂风速v_hub=25m/s，极端相关阵风期间风速的上升曲线如图3-5所示。

假定风速的上升与风向的变化量θ从0°到θ_cg的变化是同时发生的，则变化量θ_cg的计算公式为

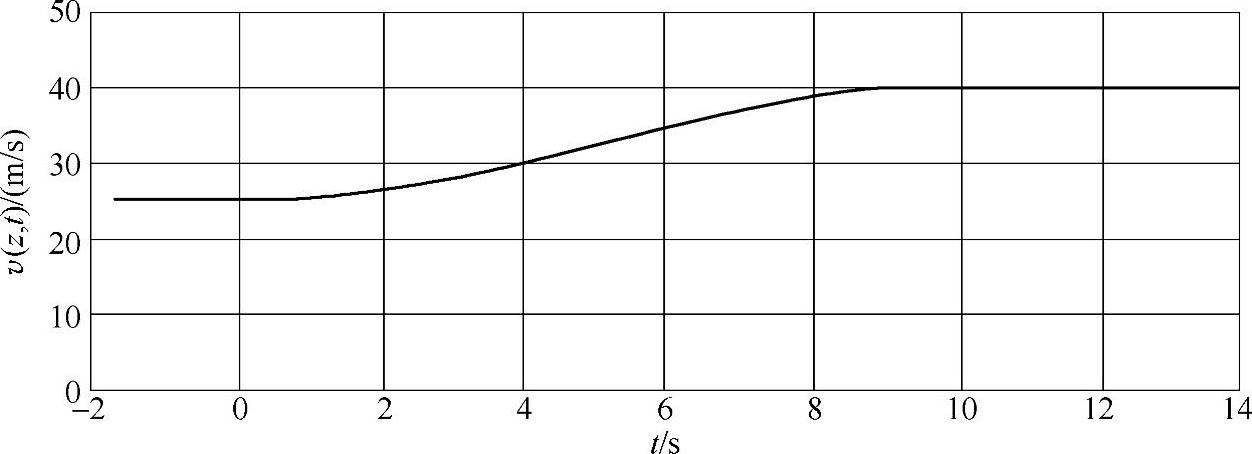
图3-5 方向改变的极端相关阵风（ECD）曲线

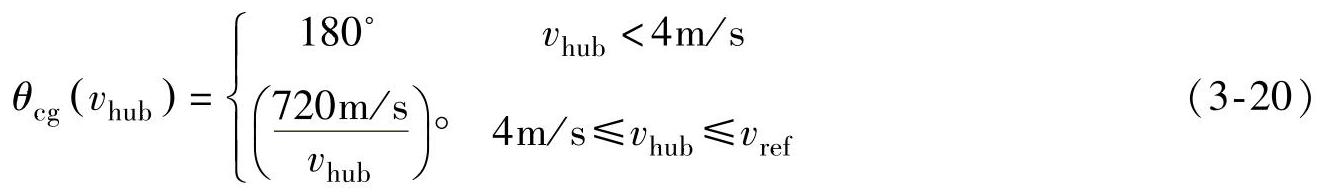
而风向同时变化角由下式给出：

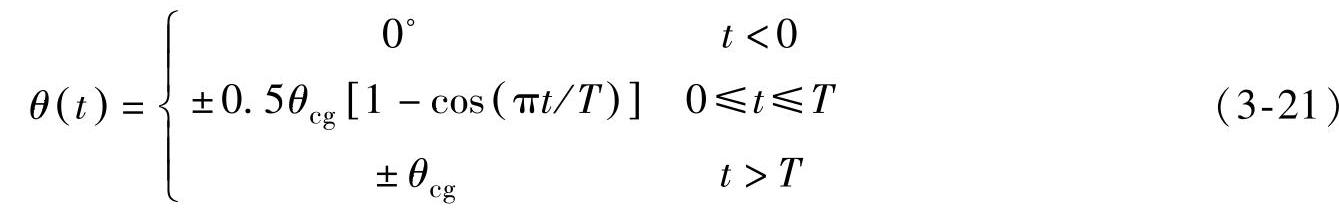
此处上升时间T=10s。

【例3-4】 风向的变化实例：假设v_hub=25m/s，风向的变化量θ_cg与轮毂高度风速v_hub的关系，风向的变化与时间的关系，分别如图3-6和图3-7所示。

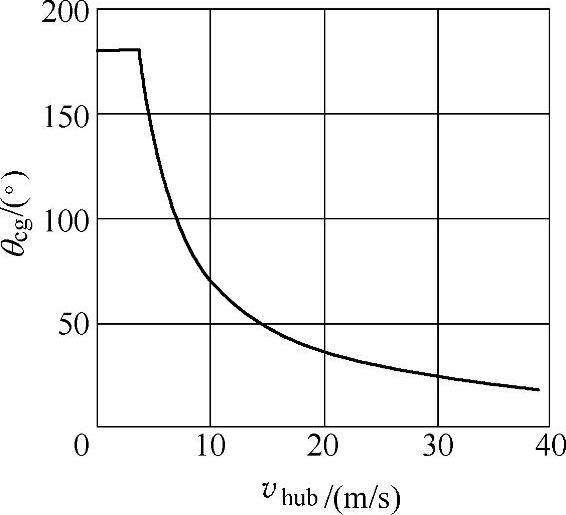
图3-6 ECD风向变化

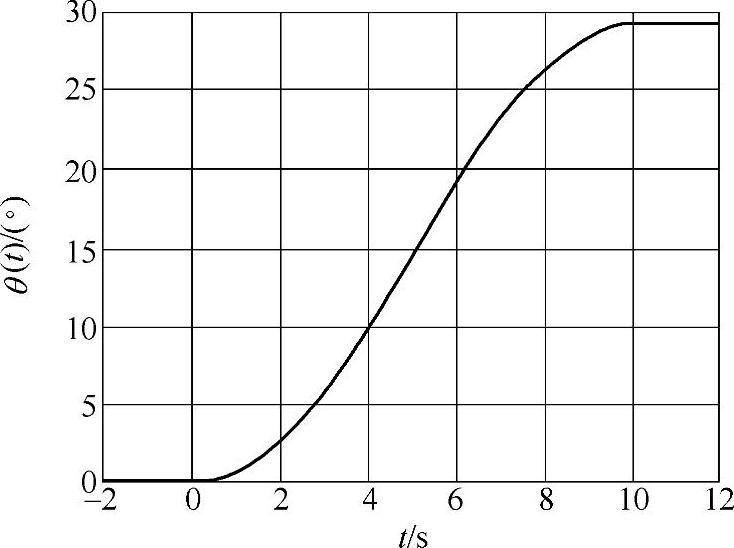
图3-7 v_hub=25m/s时风向随时间的变化

（6）极端风切变（EWS）应用下列两种瞬时风速来计算极端风切变。

1）瞬时竖直方向切变（正向或逆向）

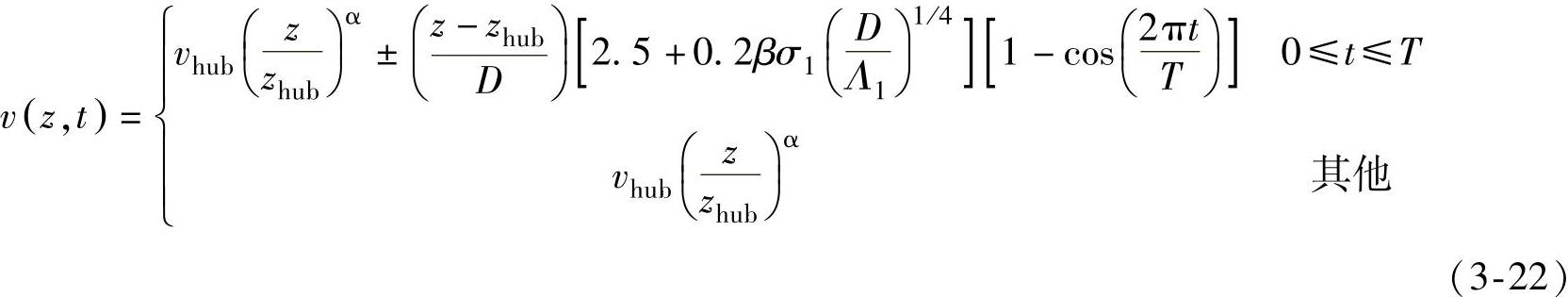
2）瞬时水平切变

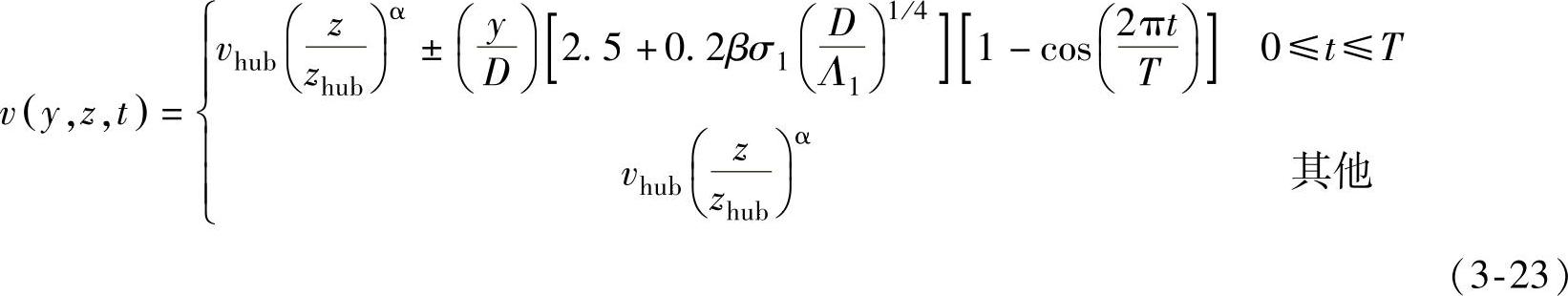
式中 α=0.2，β=6.4，T=12s；

σ₁——正常湍流模型中的湍流标准差，见式（3-7）；

Λ₁——湍流尺度参数，单位为m，见式（3-1）；

D——风轮直径，单位为m。

水平风切变瞬态符号应由最恶劣瞬时载荷发生决定。两个极端风切变不能同时应用。

【例3-5】 极端竖直风切变和风轮顶部和底部风速随时间的变化实例：如果湍流种类为A，z_hub=30m，v_hub=25m/s，D=42m，极端竖直风切变如图3-8所示。在图3-8中虚线表示的是极端风速发生前（t=0s）的风廓线，实线表示的是最大风切变（t=6s）时的风廓线，点划线表示的是负风切变（t=6s）时的风廓线。在与图3-8同样假设下，风轮顶部和底部风速随时间的变化如图3-9所示。

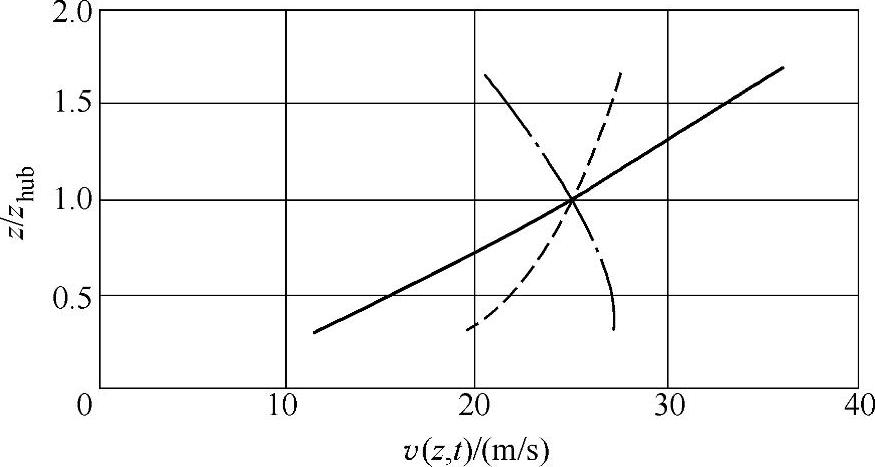
图3-8 极端正负竖直风切变的风廓线，在开始前（t=0，虚线）和最大切变（t=6s，实线）

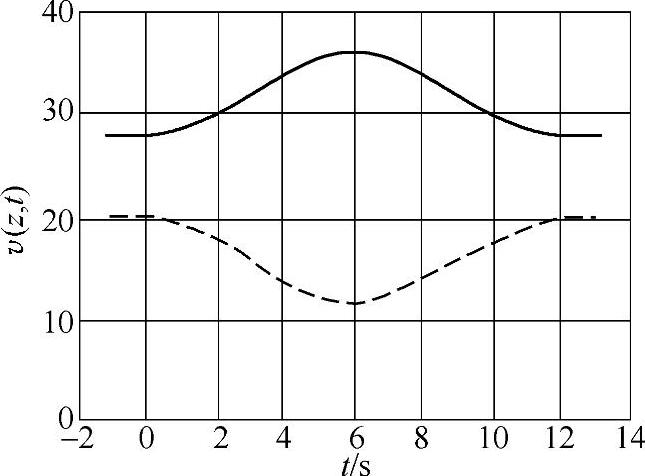
图3-9 风轮顶部及底部风速随时间的变化（瞬时正风切变）