交流发电机的基本方程式:电压、功率、转矩

在以上分析的基础上，可以写出交流发电机的基本方程式，包括电压方程式、功率方程式和转矩方程式。基本方程式是分析计算发电机性能所依据的基本原理。为了使基本方程式形式简明且具有统一性，这里采用了矩阵形式。

1.电压方程式

根据式（2-89），交流发电机的感应电动势e包括两个分量，即运动电动势分量和变压器电动势分量，因此感应电动势的矩阵形式如下式：

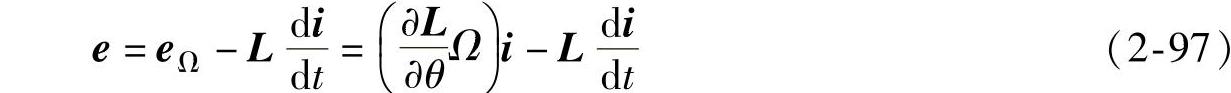
式中 e_Ω——运动电动势矩阵，；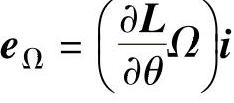

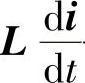——变压器电动势矩阵。具有n个绕组的交流发电机的电压方程式（2-91）可用矩阵表示为

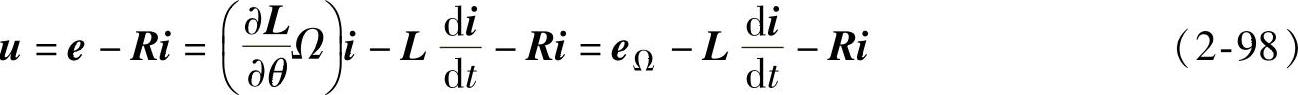
式中u，i——发电机绕组的相电压矩阵和相电流矩阵，即

其中 u_s、i_s——定子相电压和相电流矩阵，

u_r、i_r——转子相电压和相电流矩阵；

R——发电机绕组的电阻矩阵，这是一个对角矩阵，即

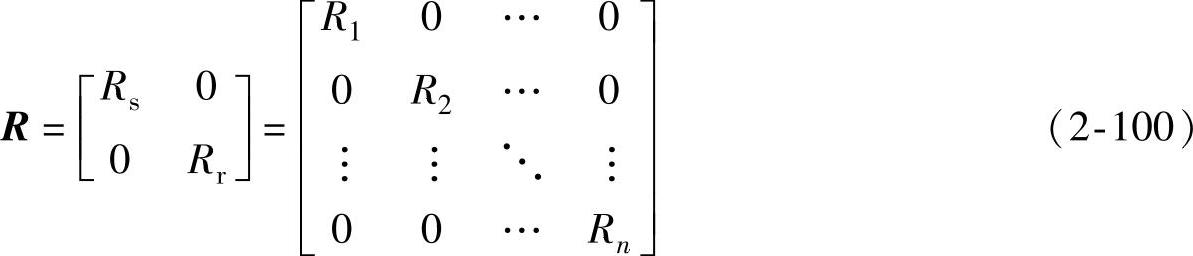
其中 R_s——定子绕组电阻矩阵；

R_r——转子绕组电阻矩阵。

L——发电机的绕组电感矩阵，一般说来，绕组电感是转角θ的函数。假定1～m为定子绕组，（m+1）～n为转子绕组，即

其中 L_ss——定子绕组电感矩阵；

L_rr——转子绕组电感矩阵；

L_sr和L_rs——定、转子绕组之间的互感矩阵。

2.功率方程式

重新观察图2-12可知，在发电机进行机电能量转换过程中，耦合场在吸收从原动机（风力机）输入的机械能并将其转变为磁场储能的变化之外，还将一部分机械能转换成电能并传递到电系统。下面就来定量讨论这一问题。

将式（2-93）所示的发电机能量关系的微分方程改写成功率方程：(www.xing528.com)

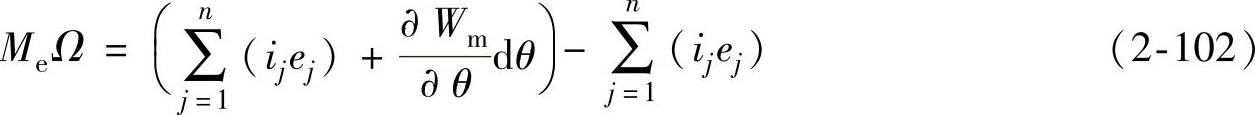
式中Ω——发电机转子的机械角速度，；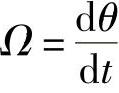

e_j——第j个绕组的感应电动势，。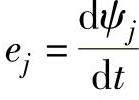

将上式改写成矩阵形式，即

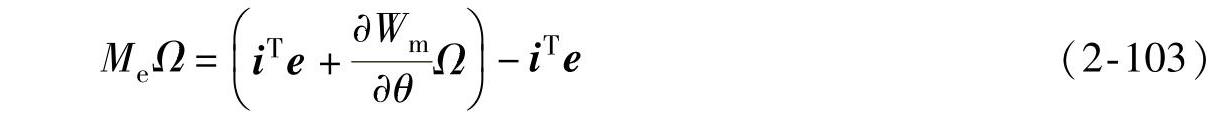
由式（2-103）可以看出，发电机从原动机（风力机）吸收的净机械功率M_eΩ中，一部分转换成磁场储能功率，即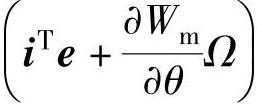，另一部分则转换成电功率i^Te输出，由机械功率直接转换成电功率的这部分功率称为发电机的转换功率。由式（2-103）还可看出，磁场储能功率包括两部分，由角位移的变化（即转子旋转运动）所引起的磁场储能功率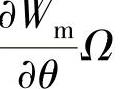恰好等于从原动机（风力机）吸收的净机械功率，即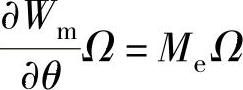；而由磁链变化所引起的磁场储能功率i^Te则恰好等于输出电功率的负值。将式（2-98）等号两边同时乘以电流i的转置矩阵i^T，就可以得到发电机电系统的功率方程式，即

式中 i^Tu——发电机线端输出的电功率；

i^Te_Ω——被绕组运动电动势吸收的电功率；

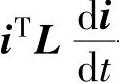——被绕组变压器电动势吸收的电功率；

i^TRi——绕组的电阻损耗。

3.转矩方程式

对于发电机来说，需要从原动机输入机械转矩，并带动发电机转子旋转，当磁场储能随转角发生变化时，发电机将产生电磁转矩，电磁转矩是一种制动性质的转矩。当发电机稳态运行时，电磁转矩将与轴上输入的机械转矩相平衡，维持机组以恒定的转速稳定运行；当发电机动态运行时，发电机的转速将会发生变化，由于旋转系统的惯性，发电机轴上除了承受稳态运行时的输入转矩和电磁转矩之外，还将承受一个动态转矩，转速变化率越大这一动态转矩的值越大。

因此，发电机稳态运行时，其机械系统的转矩方程式为

M₁=M_e+M₀ （2-105）

式中 M₁——来自原动机的输入转矩；

M_e——发电机的电磁转矩；

M₀——与发电机的风摩损耗相对应的损耗转矩，一般说来，这一损耗转矩是转子机械角速度Ω的函数。

发电机动态运行时的转矩方程式为

式中 J——发电机旋转系统的转动惯量，单位为N·m·s；

Ω——发电机转子旋转的机械角速度，单位为rad/s。显然，当M₁＞（M_e+M₀）时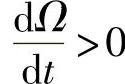，，这时发电机升速；当M₁＜（M_e+M₀）时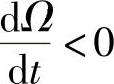，，这时发电机降速。在风力发电系统中，由于风速变化的随机性，发电机组的转速将随风速的变化而变化，使风力发电机组经常处于动态运行过程中，这是风力发电机组运行的一个特点。试想，如果由于风速的突然变大，使机组出现较大的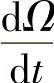，这时，机组将出现一个较大的动态转矩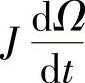，这一转矩可能是发电机额定转矩的几倍以上，可能使风力发电机组的风轮（叶片轮毂等）、传动系统（包括主轴、联轴器、齿轮箱等）以及发电机轴和底脚等受到损伤。因此，进行风力发电机组的机械系统设计时，必须充分考虑到这种动态转矩对机组安全性的影响。