传动链是机械上连接空气动力子系统和电磁子系统的一套装置。因此风转矩和电磁转矩是输入量，而转速则是输出量。假定在整个变速范围内有着恒定的机械传动效率，可以认为结构特性（例如振动、齿轮种类、齿隙等）对其性能的影响可以忽略不计。
对于典型的风力发电机组来说，组成传动链的部件有风轮、齿轮箱和发电机转子。
增速器将传动链分为两部分：与风轮直接耦合的低速轴和与发电机相连的高速轴。高速轴和低速轴之间的连接部分可以是刚性的也可以是柔性的。刚性传动链模型认为传动系统的扭转刚度足够大，即低速轴、齿轮箱的传动轴、高速轴是刚性的，转子和发电机只有一个旋转自由度，高速轴与低速轴按定传动比变化。发电机和风力机转子的加速来自于气动转矩与发电机响应转矩的不平衡。柔性传动链模型认为低速轴和高速轴是柔性的。允许风力机转子和发电机转子有各自的旋转自由度。风力机转子的加速度依赖于气动转矩和低速轴转矩之间的不平衡。发电机转子的加速度依赖于高速轴扭矩和发电机响应转矩之间的不平衡。在柔性连接中，高速轴与低速轴具有不同的瞬间转速。这种解耦是用来减少由风速或电磁转矩变化而引起的机械应力。由此，它的兼容性和传动的可靠性都大大提高，不容易受暂态负载和机械疲劳的影响。下文将分别讨论刚性模型和柔性模型。
1.刚性模型
风力发电机组主传动链刚性模型如图2-8所示。
图2-8 主传动链刚性模型
刚性传动链模型的主要组成部分是单级耦合增速器，它的传动比为i，效率为η，在这种情况下，由于增速器的作用，发电机转矩减少i倍且速度增加i倍。在上述模型假设下，在高速轴或低速轴下的风能转换系统动态模型可以由下列两个方程表示：
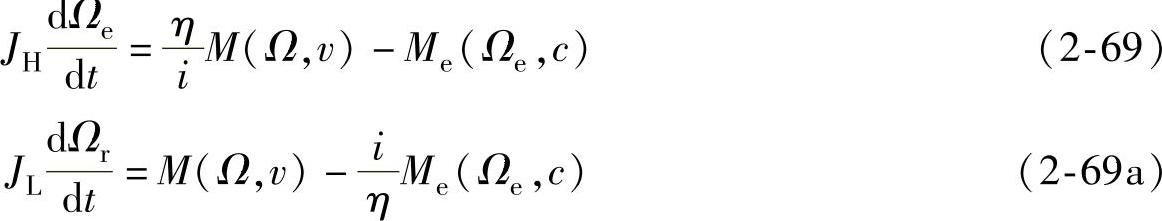
式中 Ω——风轮旋转角速度；
Ωe——发电机转子机械角速度；
M（Ω，v）——空气动力转矩，以风速v作为参数；
Me（Ωe，c）——电磁转矩，一般以c表示的负载变量作为参数；
式中 J1、J2——增速齿轮的转动惯量；
Jr、Je——风轮和发电机转子的转动惯量。
由于传动链是刚性的，空气动力转矩仅由一阶线性转速变量给定。图2-9为转换到高速轴处的运动方程的仿真框图。此方程通常用于电机组传动链单自由度模型。
图2-10给出了当高速轴以Ωe的角速度旋转时，风轮和发电机相互作用稳定运行的示意图。风力发电机组的稳定运行点是风轮和发电机机械特性曲线的交点。
(www.xing528.com)
图2-9 运动方程的仿真框图
2.柔性模型
风力发电机组主传动链柔性模型如图2-11所示。
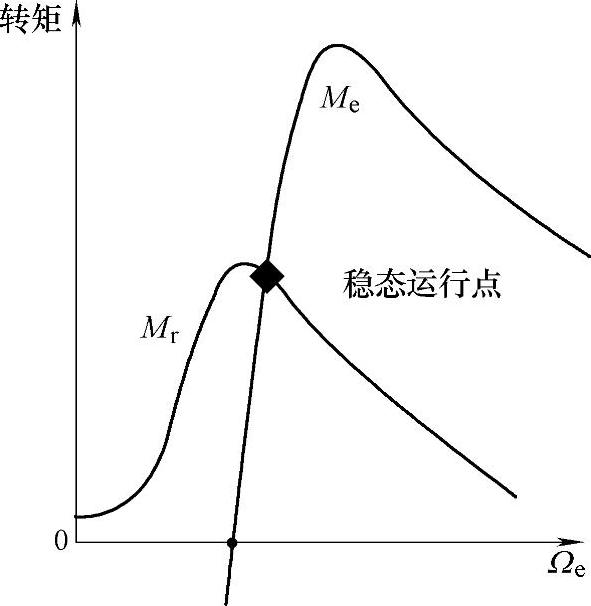
图2-10 风力发电机组稳态曲线
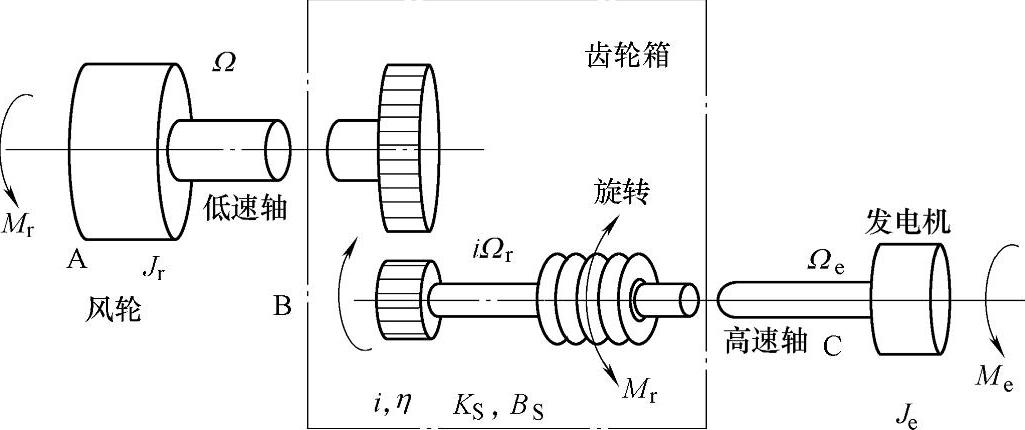
图2-11 主传动链柔性模型
高速轴的B和C两部分以不同的转速旋转，分别是iΩr和Ωe，这里i是齿轮箱的传动比。弹性能变化量产生一个新的状态变化内转矩M。Je表示C部分的惯量，JB表示B部分的惯量，表达式为
式中 η——传动效率；
Jr——低速部分（主要是风力机）的转动惯量。
传动装置柔性模型由B和C部分运动方程和内转矩动态方程构成：
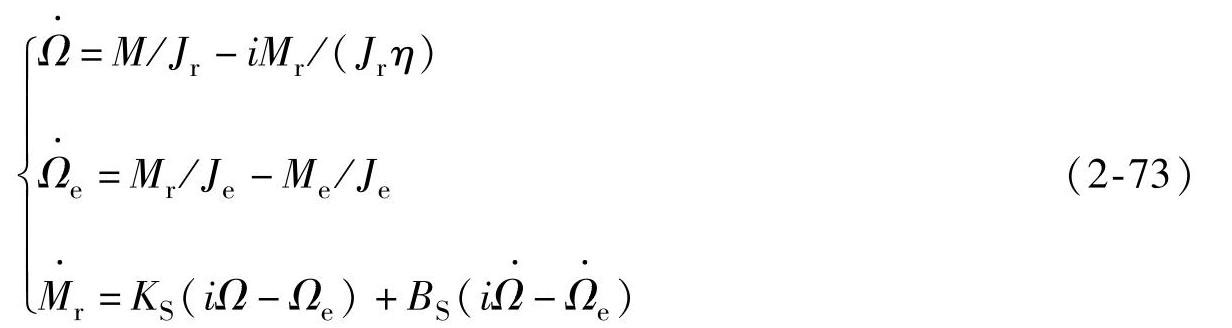
得到一个三阶线性模型，状态变量为x=[ΩrΩeM]T，输入矢量为u=[MMe]T，输出矢量为y=[ΩΩe]T，则
式中 KS、BS——弹性系统的刚性系数和阻尼系数。
上述推导过程也适合于直驱式风力发电机组的传动链，这时，状态方程变为
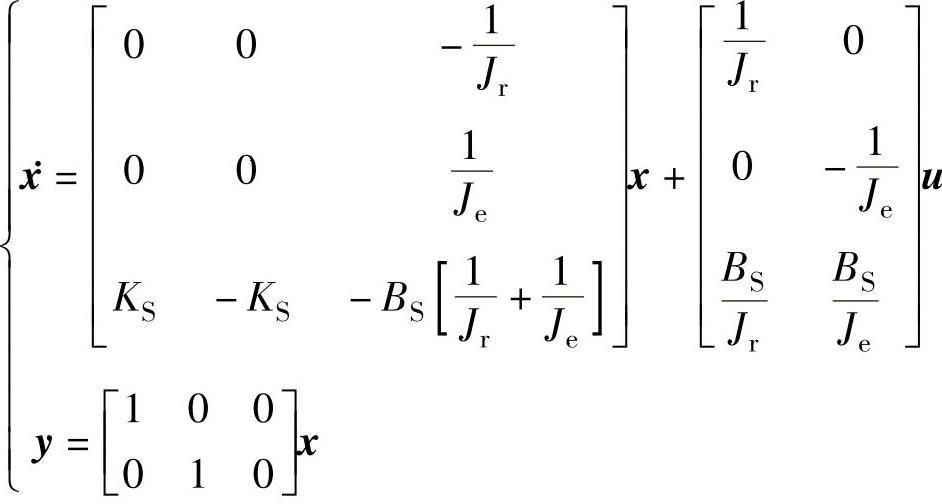
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
