弹性力学基本方程探析

在各向同性线性弹性力学中，为了求得应力、应变和位移，先对构成物体的材料以及物体的变形作了五条基本假设，即：连续性假设、均匀性假设、各向同性假设、完全弹性假设和小变形假设，然后分别从静力学、几何学和物理学方面出发，导得弹性力学的基本方程和边界条件的表达式。下列各式中，σ_x、σ_y、σ_z、τ_xy（τ_yx）、τ_yz（τ_zy）、τ_zx（τ_xz）为应力分量；u、v、w为位移矢量在三个方向的分量；ε_x、ε_y、ε_z、γ_xy、γ_yz、γ_zx分别为正应变和剪应变分量；F_bx、F_by、F_bz单位体积的体力在各方向的分量；μ为泊松比。

1.平衡微分方程

2.几何方程

物体受力后变形，其内部任一点的位移与应变的关系如下：

3.物理方程（广义虎克定律）

（1）应力表示应变

式中 E——拉压弹性模量，简称为弹性模量；

G——剪切弹性模量，简称为刚度模量，且有

（2）应变表示应力

式中 e_v——体积应变，e_v=ε_x+ε_y+ε_z。

总之，上述共有15个独立方程（3个平衡微分方程、6个几何方程、6个物理方程），包含15个未知变量（3个位移分量u、v、w、6个应力分量σ_x、σ_y、σ_z、τ_xy（τ_yx）、τ_yz（τ_zy）、τ_zx（τ_xz）、6个形变分量ε_x、ε_y、ε_z、γ_xy、γ_yz、γ_zx）。给定边界条件后方程组有定解。

4.边界条件

若物体表面的面力分量为F_sx、F_sy和F_sz已知，则表面力边界条件为

F_sx=σ_xl+τ_xym+τ_xzn(www.xing528.com)

F_sy=τ_xyl+σym+τ_zyn

F_sz=τ_xzl+τ_yzm+σ_zn （2-67）

式中 l、m、n——物体表面外法线的三个方向余弦。

若物体表面的位移已知，则位移边界条件为

式中 u_s、v_s、w_s——位移的边界值；

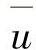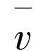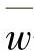、、——在边界上是坐标的已知函数。

5.基本方程的求解

在求解弹性力学问题时，并不需要同时求解15个基本未知量，可以做必要的简化。为简化求解的难度，仅选取部分未知量作为基本未知量。在给定的边界条件下，求解偏微分方程组的问题，数学上称为偏微分方程的边值问题。

按照不同的边界条件，弹性力学有三类边值问题。

第一类边值问题：已知弹性体内的体力和其表面的面力分量为F_sx、F_sy和F_sz，边界条件为面力边界条件。

第二类边值问题：已知弹性体内的体力分量以及表面的位移分量，边界条件为位移边界条件。

第三类边值问题：已知弹性体内的体力分量，以及物体表面的部分位移分量和部分面力分量，边界条件在面力已知的部分，为面力边界条件，位移已知的部分为位移边界条件，称为混合边界条件。

以上三类边值问题，代表了一些简化的实际工程问题。若不考虑物体的刚体位移，则三类边值问题的解是唯一的。