1.贝兹极限
贝兹极限是由德国的空气动力学家贝兹(Albert Betz)提出的。假定风轮是理想的,即
1)风轮可以简化成一个平面桨盘,没有轮毂,而叶片数无穷多,这个平面桨盘被称为致动盘;
2)风轮叶片旋转时不受摩擦阻力,是一个不产生损耗的能量转换器;
3)风轮前、风轮扫掠面、风轮后气流都是均匀的定常流,气流流动模型可简化成图2-1所示的流束;
4)风轮前未受扰动的气流静压和风轮后远方的气流静压相等;
5)作用在风轮上的推力是均匀的;
6)不考虑风轮后的尾流旋转。
此时,空气流过致动盘的瞬时能量转换可由图2-1表达。致动盘前部的远方来流通过致动盘时,受风轮阻挡被向外挤压,绕过致动盘的空气能量未被利用。只有通过致动盘截面的气流释放了所携带的部分动能。致动盘上游流束的横截面积比致动盘面积小,而下游的则比致动盘面积大。流束膨胀是因为要保证每处的质量流量相等。
由于风速远小于当地空气的声速,即运动气流的马赫数Ma<<1,空气的压缩性可被忽略。
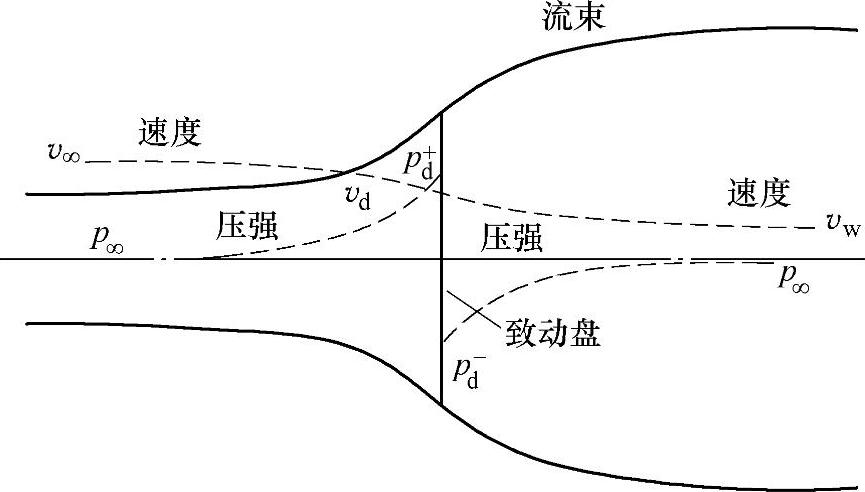
图2-1 流经致动盘的流束
单位时间内通过特定截面的空气质量是ρAv,其中ρ为空气密度(kg/m3),A为横截面积(m2),v为流体速度(m/s)。沿流束方向的质量流量处处相等,可得
ρA∞v∞=ρAdvd=ρAwvw (2-7)
式中下角标的含义是∞——上游无穷远处的参数;
d——致动盘处的参数;
w——尾流远端的参数。
致动盘导致气流速度发生变化,该速度变化将叠加到自由流速率上。该诱导气流在气流方向的分量为-av∞,其中a为轴向气流诱导因子。所以在致动盘上,气流方向的净速度为
vd=v∞(1-a) (2-8)
由此,在致动盘面处,轴向气流诱导因子

气流在经过致动盘时速度发生变化,总变化量为(v∞-vw),根据动量定理,气流所受的作用力等于动量变化率,动量变化率等于速度的变化乘以质量流量,即
F=(v∞-vw)ρAdvd (2-10)
式中 F——气流所受的作用力,单位为N。
引起动量变化的力完全来自于致动盘前后静压力的改变,所以有:
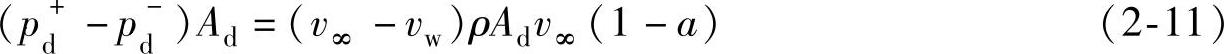
式中 p+d——致动盘前气流静压,单位为Pa;
p-d——致动盘后气流静压,单位为Pa。
对流束的上风向和下风向分别使用伯努利方程,可以求得压力差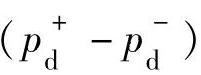 。对上风向气流有
。对上风向气流有
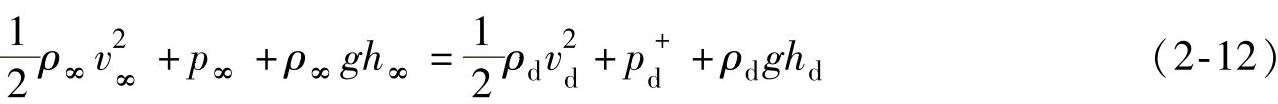
由于假设气体是不可压缩,ρ∞=ρd,并且流束处于水平方向,高度h∞=hd,那么有

同样下风向气流有

方程(2-13)和方程(2-14)相减得到:

把方程(2-15)代入(2-11)得到:
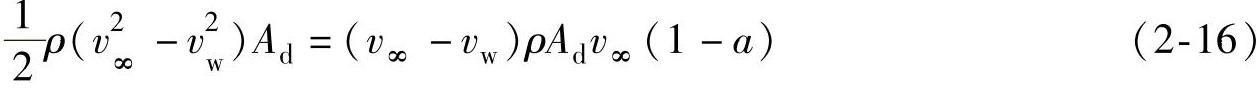
因此
vw=(1-2a)v∞ (2-17)致动盘作用在气流上的力,可由方程(2-17)代入方程(2-10)导出:
F=(p+d-p-d)Ad=2ρAdv2∞a(1-a) (2-18)
这个力在数值上等于气流对致动盘的反作用力,因此气体输出功率
P=Fvd=2ρAdv3∞a(1-a)2 (2-19)
定义风能利用系数

其中分母表示横截面积为Ad的自由流束所具有的风功率。将式(2-19)代入式(2-20)得
CP=4a(1-a)2 (2-21)
可以求出,当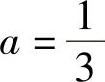 时,CP的值最大。将
时,CP的值最大。将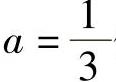 代入方程(2-21)得
代入方程(2-21)得

这个值称为贝兹极限。它是水平轴风机的风能利用系数的最大值。
由压力降产生的作用于致动盘的力T与致动盘作用在气流上的力大小相等,所以T可以由式(2-18)求得。定义无量纲的推力系数

将式(2-18)代入式(2-23),得
CT=4a(1-a) (2-24)
尾流速度为(1-2a)v∞,当a≥1/2时,将出现尾流速度变成零,甚至变成负数的问题。在这种情况下,上述模型将不再适用。
风能利用系数和推力系数随a的变化曲线如图2-2所示。
2.旋转尾流模型
贝兹极限所讨论的气流模型只考虑轴向流动。这里将进一步考虑旋转尾流问题。仍然沿用致动盘的基本假设,但更为具体的将致动盘描述为多个叶片扫过的区域,或称为风轮圆盘。
气流通过风轮圆盘时,圆盘所受转矩与作用在空气上的转矩大小相等、方向相反。反转矩作用的结果会导致空气逆着风轮转向旋转,从而获得角动量,这样会使风轮圆盘尾流的空气微粒在旋转面的切线方向和轴向上都获得了速度分量如图2-3所示。
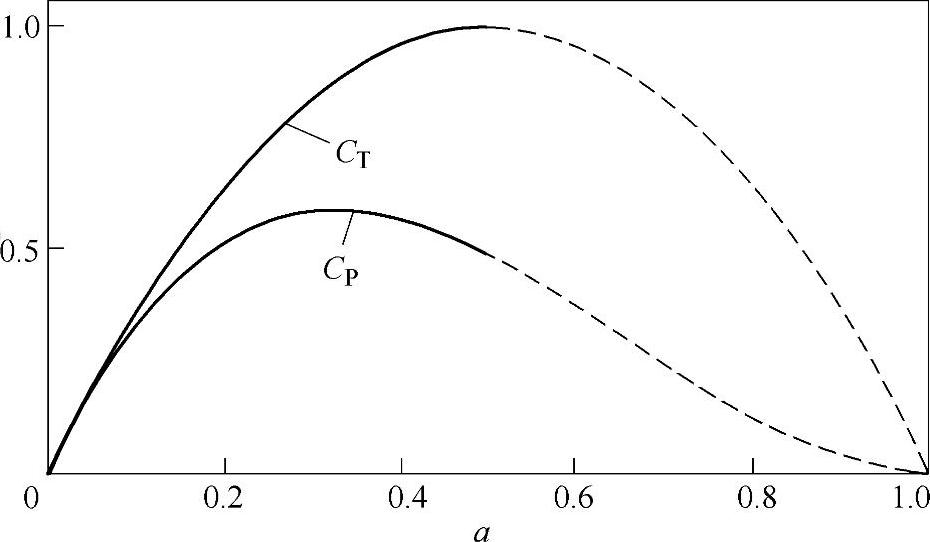
图2-2 CP、CT随a的变化曲线
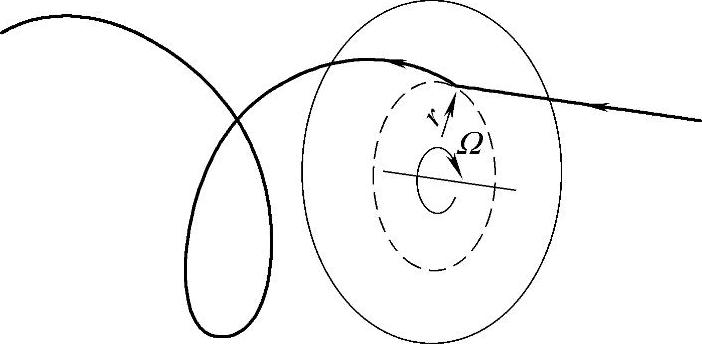
图2-3 空气微粒经过风轮圆盘的运动轨迹
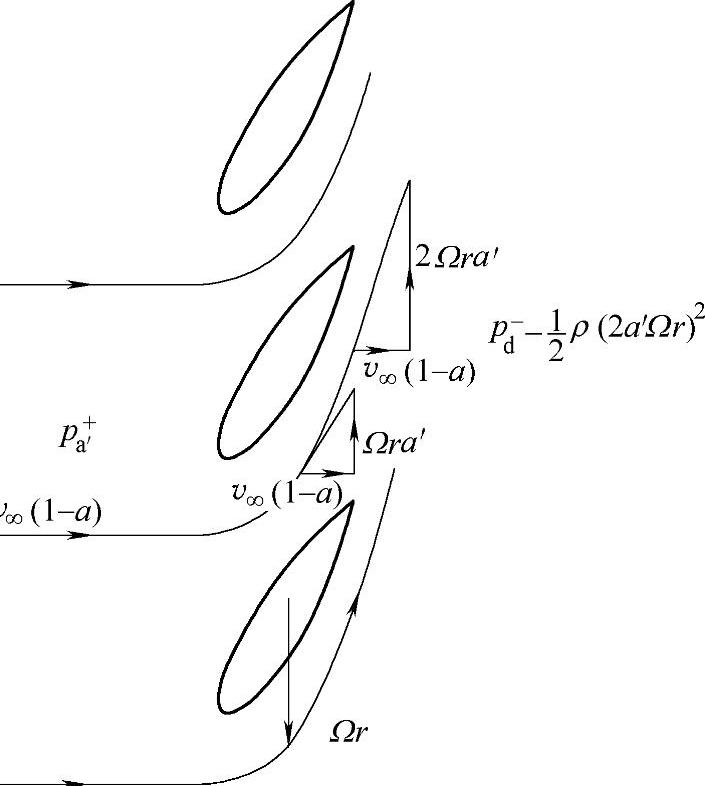
图2-4 气流切向速度在通过圆盘的变化
进入圆盘的气流无任何转动,而离开圆盘的气流是旋转的。转动传递发生在整个圆盘的厚度处,如图2-4所示。切向速度的变化用切向气流诱导因子a′表示。圆盘上游气流的切向速度为零。设风轮旋转角速度为Ω,圆盘下游在距旋转轴径向距离为r的地方气流切向速度为2Ωra′。在圆盘厚度中部,切向诱导速度为Ωra′。
在所有的各个径向位置上,切向速度是不同的,轴向诱导速度也不一样。为了讨论圆盘的动力学特性,截取半径为r、径向宽度为δr的圆环(见图2-5),整个圆盘由多个圆环组成,并且假定每个环的作用力相互独立。
圆环反作用于空气的转矩,将使空气产生切向速度分量,而作用在圆环上的轴向力将会使空气轴向速度降低。
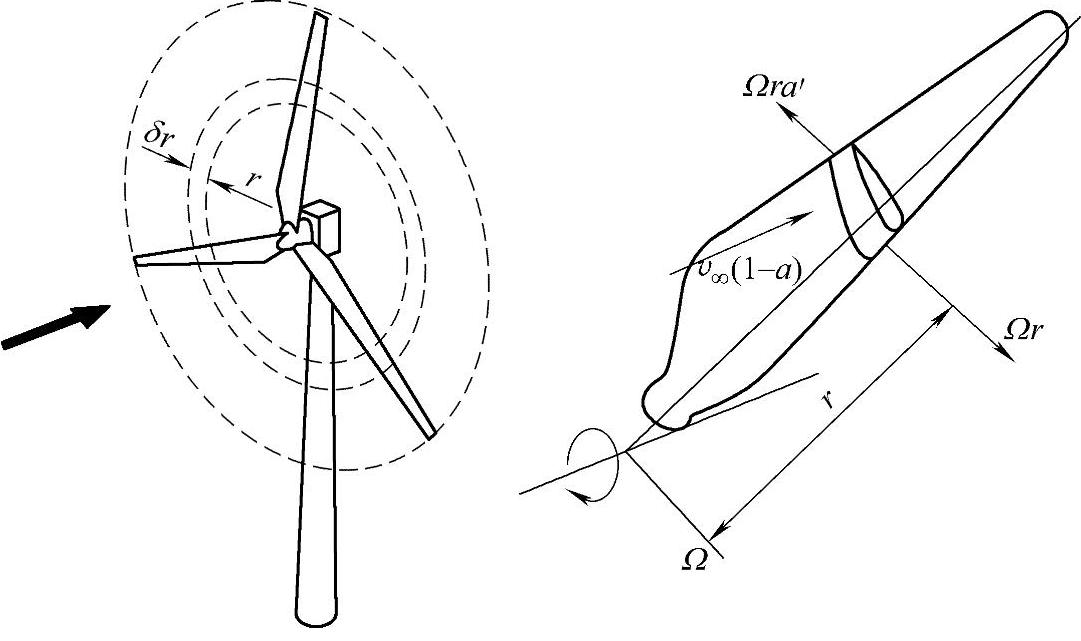
图2-5 叶素扫出的圆环
作用在圆环上的转矩与圆环反作用于空气的转矩大小相等,而作用于空气的转矩等于通过此环形区的空气的角动量的变化率,即
dM=2Ωra′rdṁ
式中 dṁ——单位时间流经圆环上的空气流量。
dṁ=ρv∞(1-a)dAd (2-25)
考虑到圆环的面积dAd=2πrdr,可得作用在圆环上的转矩为
dM=4πρΩv∞(1-a)a′r3dr( 2-26)
所以风轮转轴输出的功率增量为
dP=ΩdM (2-27)
风速降低所输出的功率由式(2-19)给出。即
dP=2ρv3∞a(1-a)2dAd (2-28)
因此,由式(2-26)、式(2-27)和式(2-28)有
2ρv3∞a(1-a)2dAd=ρv∞(1-a)2Ω2a′r2dAd
和
v2∞a(1-a)=Ω2r2a′ (2-29)
其中,Ωr为旋转圆环的切向速度,所以λr=Ωr/v∞称为当地速度比。在圆盘r=R的边缘处,λ=ΩR/v∞称为叶尖速度比。因此
a(1-a)=λ2ra′ (2-30)
从式(2-26)、式(2-27)中可以得出:
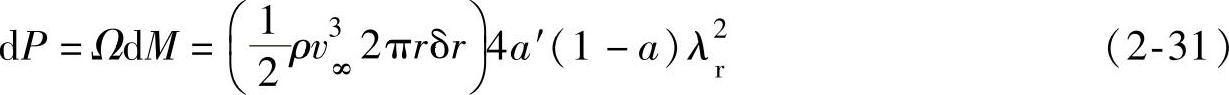 (https://www.xing528.com)
(https://www.xing528.com)
式(2-31)右边括号里的部分表示通过圆环的功率流量,括号外的部分被称为捕获功率时叶片单元效率,即
ηr=4a′(1-a)λ2r (2-32)
将式(2-30)代入式(2-32),得
ηr=4a(1-a)2 (2-33)
风能利用系数变化率可表示为
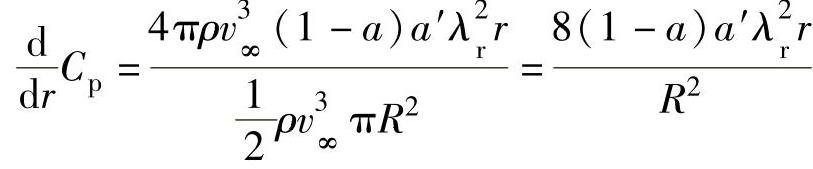
即

其中,μ=r/R。
如果知道a和a′沿径向的变化规律,那么对于给定的叶尖速度比λ,通过对式(2-34)进行积分可以确定总的风能利用系数。
能提供最大可能效率的a和a′值是通过求式(2-32)对a′的导数,并令其结果等于零而得到的。由此
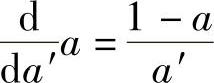
对于式(2-30)求导也有
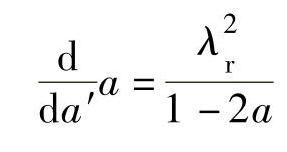
得到

联立式(2-30)和式(2-35),可以求出使风能利用系数最大的a和a′的值为

最大功率输出的轴流诱导因子也与非旋转尾流的情况一样,都是a=1/3,并且在整个圆盘上都是一致的。a′却随着径向位置的变化而变化。
从式(2-34)可以得到最大功率系数为
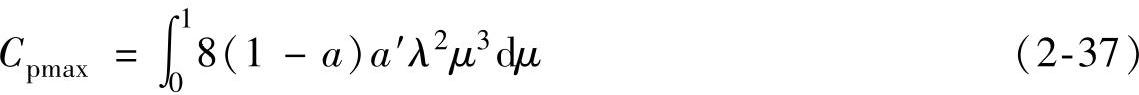
将式(2-36)代入式(2-37),得
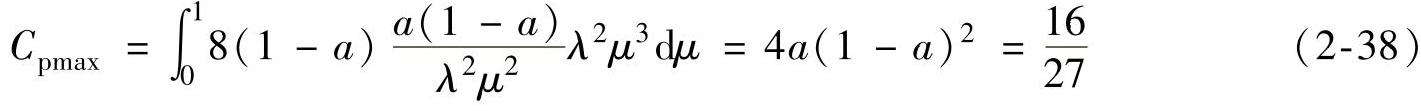
这与非旋转尾流的模型正好相同。
传递给尾流的角动量增加了尾流的动能,但该能量被静压损失所平衡。即

将式(2-36)代入式(2-39),得
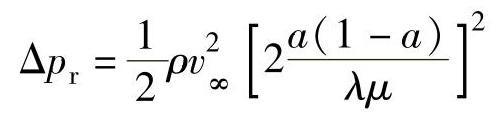
3.叶素—动量定理
在叶片上,取半径为r、长度为δr的微元,称为叶素(见图2-5)。在风轮旋转过程中,叶素将扫掠出一个圆环。
对于一个叶片数为N、风轮半径为R、弦长为c、叶素桨距角(叶素几何弦线与风轮旋转面间的夹角)为β的风力机,弦长和桨距角都沿着桨叶轴线变化。令风轮的旋转角速度为Ω,风速为v∞。同时考虑到尾流旋转,圆盘下游在距旋转轴径向距离为r的地方气流以2Ωra′(a′为切向气流诱导因子)的切向速度旋转。叶素的切向速度Ωr与圆盘厚度中部气流的切向速度Ωra′之和为经过叶素的净切向流速度Ωr(1+a′)。图2-6示出了在半径为r处叶素上的速度和作用力。
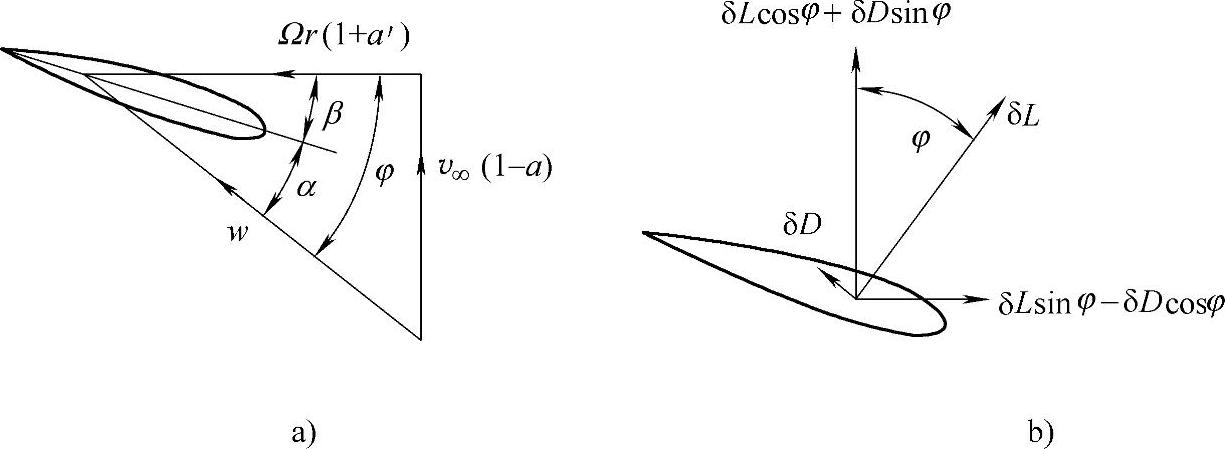
图2-6 叶素上的速度和作用力
a)速度 b)作用力
从图2-6中得到的叶片上的相对合速度为
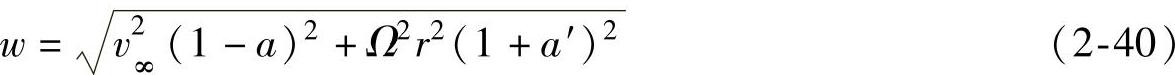
相对合速度与旋转面之间的夹角(气流倾角)是φ,则

攻角α由下式给出
α=φ-β (2-43)
每个叶片在顺翼展方向长度为δr的升力

式中 ρ——空气密度,单位为kg/m2;
w——相对风速,单位为m/s;
c——几何弦长,单位为m;
Cl——翼型升力特征系数。
平行于w的阻力为

式中 Cd——翼型阻力特征系数。
假定作用于叶素上的力仅与通过叶素扫过的圆环的气体的动量变化有关。而通过邻近圆环的气流之间不发生径向相互作用。
N个叶素上的空气动力分量在轴向上分解为
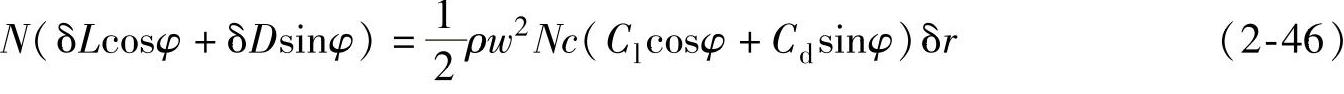
通过扫掠圆环面积的轴向动量变化率为
2av∞ρv∞(1-a)2πrδr=4πρv2∞a(1-a)rδr (2-47)
尾流旋转导致的尾流压力下降等于动力压头的增加,因此在圆环上附加的轴向力为

气流对扫掠圆环的作用力数值上等于圆环的反作用力,根据动量定理,这个反作用力等于气流动量的变化率。从式(2-46)、式(2-47)和式(2-48)可得
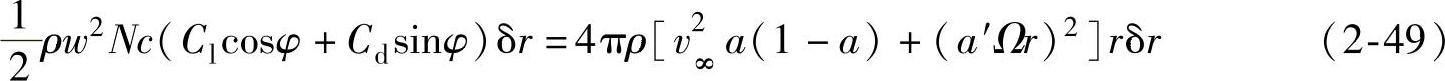
化简为
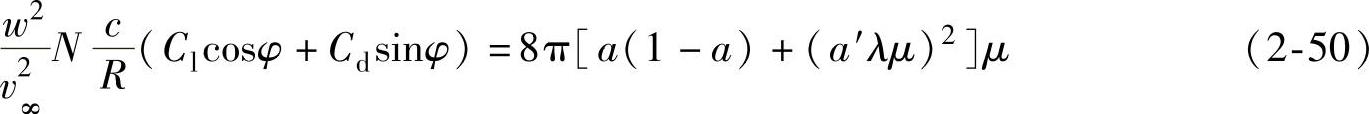
其中,μ=r/R,λ=ΩR/v∞。
N个叶素上空气动力产生的风轮轴向转矩为
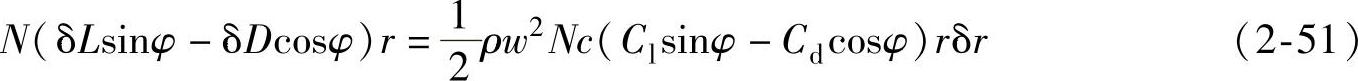
通过圆环的空气角动量变化率为
2a′Ωr2ρv∞(1-a)2πrδr=4πρv∞(Ωr)a′(1-a)r2δr (2-52)
根据动量定理,轴向转矩与角动量变化率相等,从式(2-51)和式(2-52)可得
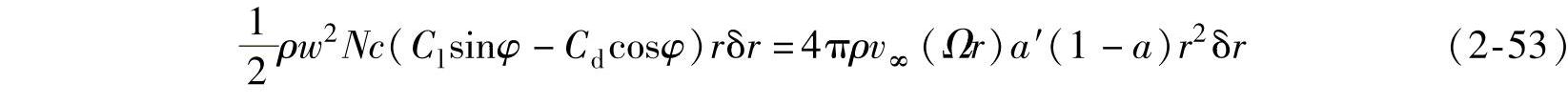
化简为
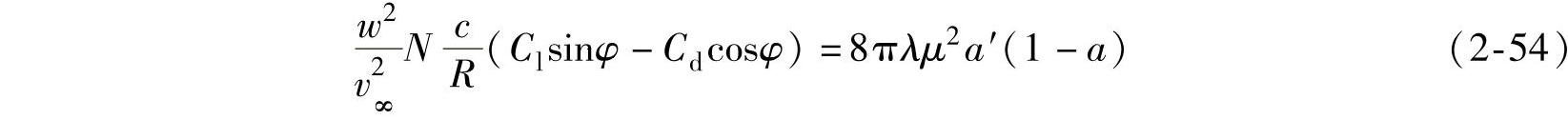
设
Clcosφ+Cdsinφ=Cn (2-55)
Clsinφ-Cdcosφ=Ct (2-56)
由式(2-50)和式(2-54)可以得了气流诱导因子a和a′。利用二维翼型特性求解a和a′是需要有迭代过程的。迭代方程如下:
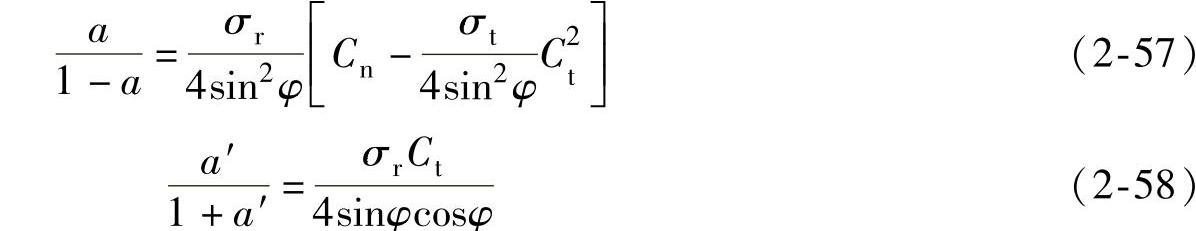
式中 σr——弦长实度。定义为给定半径下的总叶片弦长除以该半径的周长。即

从式(2-52)可以得到展向长度为δr的叶素产生的转矩为
δM=4πρv∞(Ωr)a′(1-a)r2δr (2-60)
因此,整个转子产生的总转矩为
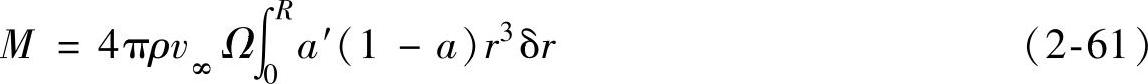
风轮产生的功率P=MΩ,风能利用系数是

4.风力机转矩计算流程
风力机转矩可以由上述各公式计算获得,其流程如图2-7所示。
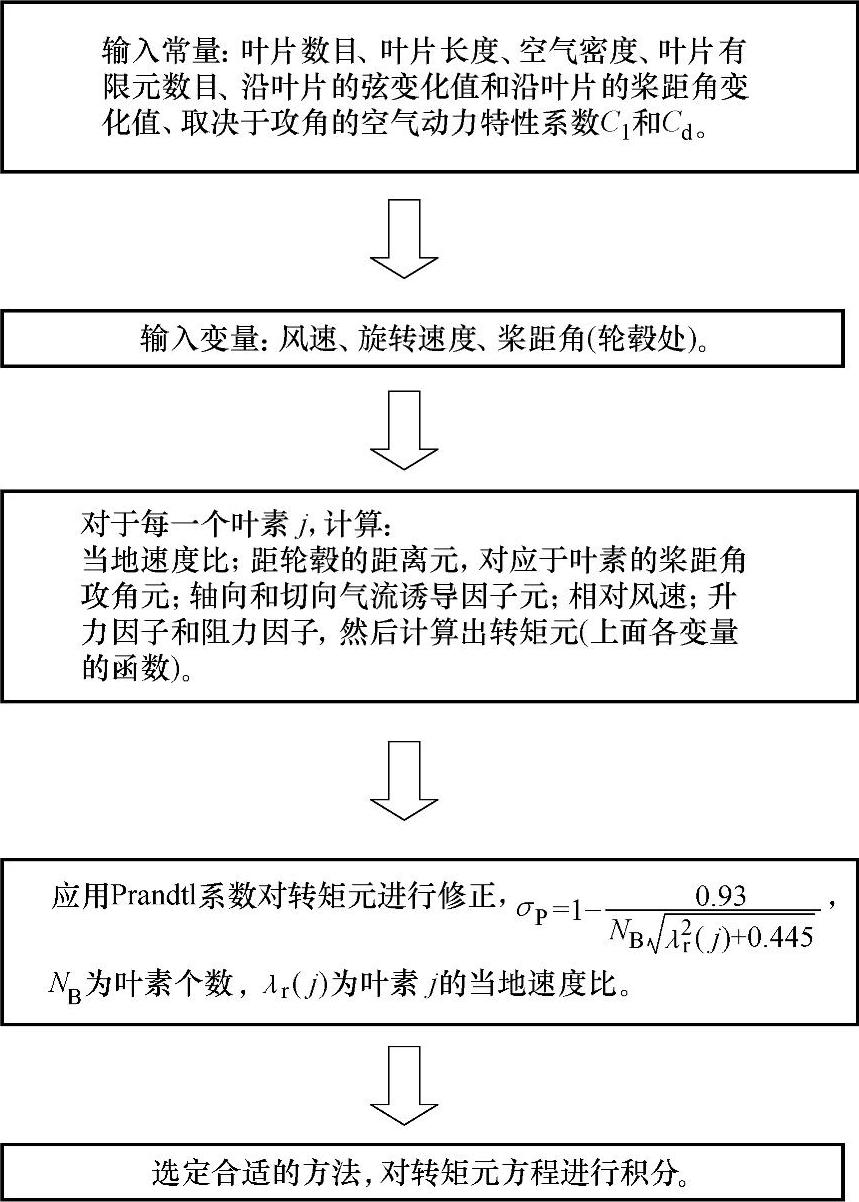
图2-7 风力机转矩计算流程
图2-7中的Prandtl系数σP是考虑到在计算中叶素的个数是有限的,从而引入的一个修正系数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




