流体力学基本方程简介

流体所流过的相对于某个坐标系来说是固定不变的任何体积称之为控制体。控制方程可通过对两种“控制体”应用基本物理规律导出，分别为固定在流场空间的控制体和随流体一起运动的控制体。常用的是前一种控制体得到的控制方程。

1.流体力学的控制方程

这里介绍的流体力学控制方程组中物理量符号含义如下：ρ为流体密度；V为流体速度矢量，u、v、w为速度矢量在三个方向的分量；P为压强；τ_xx、τ_yy、τ_zz、τ_xy（τ_yx）、τ_yz（τ_zy）、τ_zx（τ_xz）为切应力（下标规定：第一个下标代表应力所在平面的外法线方向，第二个下标代表应力的方向。例如，τ_xy表示作用在与X轴垂直的平面上沿Y方向的切应力）；f为单位质量流体的质量力，f_x、f_y、f_z为单位质量流体的质量力的分量；e为单位质量流体的微观分子运动的动能（内能）；T为流场绝对温度。

（1）连续方程

连续性方程是质量守恒定律在运动流体中的数学表达式。质量守恒定律表述如下：控制体内流体质量的减少量应等于从控制体净流出的流体质量。连续方程的矢量形式为

在直角坐标系中，连续性方程式为

（2）运动方程（纳维-斯托克斯方程）

运动方程是动量守恒定律对于运动流体的表达式。运动方程的矢量形式为

式中 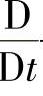——质点导数符号，且有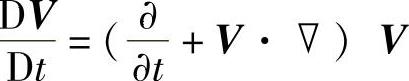，即为质点加速度；

[τ]——应力张量，其定义为

在直角坐标系中，运动方程可写成

根据广义牛顿定律，有下列关系式：

式中 μ——流体动力黏度；

λ——膨胀黏性系数，。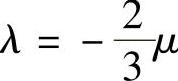

将这些关系式代入式（2-2a）、（2-2b）、和（2-2c），运动方程变为

（3）能量方程

能量方程是能量守恒定律对于运动流体的表达式。用内能表示的能量方程的矢量形式为

式中 q——由于热幅射或其他原因在单位时间内传入单位质量流体的热量；

k——导热系数。

[ε]——变形率张量，其定义为

变形率张量的分量表示变形速度，在直角坐标系中，线变形速度为

剪切变形速度为(www.xing528.com)

式（2-3）的物理意义是：在单位时间内，单位体积流体内能的增加等于单位体积内由于流体变形表面力所做的功[τ]·[ε]，加上热传导及由于热辐射等其他原因传入的热量[∇·（k∇T）+ρq]。

在直角坐标系中，能量方程可写成

2.补充方程

1）假设气体是完全气体，有状态方程

p=ρRT （2-4）

式中 R——气体常数。

2）流体的状态热力学关系式

式中 c_v——定容比热，且有

c_v=c_v（T） （2-6）

总之，上述共有7个独立方程（1个连续方程、3个运动方程、1个能量方程、2个补充方程），包含7个流场未知变量，即ρ、p、u、v、w、T、e，给定边界条件和初始条件后方程组有定解。

3.边界条件

如果给定边界条件和初始条件（初值），可以求得控制方程的特解。

（1）黏性流体边界条件

假定物面和气体直接接触表面无相对速度，叫无滑移边界条件。对静止物体有

u=v=w=0（在物面上）

（2）无黏流体边界条件

流动在物面有滑移，在物面上，流动一定与物面相切。

V·n=0（在物面上）

应该指出，为了更具一般性，上述基本方程的推导中把密度ρ视为变量。实际上，在风速范围内，是可以把ρ视为常数的。

4.控制方程组离散和有限差分解

有限差分法被广泛地应用在计算流体力学中。其原理是，用有限差分表达式来代替流体力学控制方程中出现的偏导数，从而生成控制方程的差分方程。用网格离散流场在网格单元应用差分形式的控制方程，最后生成一个与流场离散节点数相等的大型代数方程组（控制方程离散）。给定边界条件和初值条件，解大型代数方程组，就得到离散网格节点上流场变量的数值解。