本节着重介绍黑体的辐射特性,即在不同温度下黑体的单色辐射力随波长的变化规律,黑体的辐射力与绝对温度的关系,以及黑体表面辐射能量按空间方向的分布规律。本节还介绍物体的辐射特性,即物体的辐射力与吸收率之间的关系,以及灰体的概念。
一、普朗特定律
普朗特定律(1901年)揭示了在各种不同温度下绝对黑体的单色辐射力按波长变化的规律,即E0,λ=f(λ,T)。普朗特用量子理论确定了这一函数关系为
式中:λ——波长,m;
T——物体的热力学温度,K;
e——自然对数的底数;
C1——普朗特定律第一常数,等于3.743×10﹣16W·m2;
C2——普朗特定律第二常数,等于1.4387×10﹣2m·K。
普朗特定律可以用图17-4中的曲线来表示。
图17-4 普朗特定律所揭示的关系E0,λ=f(λ,T)
由图可以看出,在某一温度下λ=0时, E0,λ=0,随着波长的增加,在某一数值λm时,E0,λ达到最高值,然后又随看λ的增加而逐渐增小,直到λ=∞时E0,λ又重新降为零。
二、维恩位移定律
仔细观察图17-4可以发现,黑体在不同温度下的单色辐射力的最高峰是随着温度增高而移向波长较短的一边。这一点可以用下列简单的实验来证明,把一块铁渐渐加热至发光,首先它呈现红色,随着温度升高,逐渐变为黄色,物体的温度超过1300℃时将出现所谓的白炽,它变为白色,这是因为红色可见光的波长比黄色的长。
维恩总结出:在一定温度下,对应于最大单色辐射力的波长λ,与该黑体热力学温度T成反比,即“维恩位移定律”为
三、斯蒂芬-波尔兹曼定律
1879年斯蒂芬用实验方法确定了绝对黑体的辐射力与其本身热力学温度的四次方成正比,即E0∞T4。1884年波尔兹曼从理论上证明E0=σ0T4。σ0=5.669×10﹣8W/(m2·K4),称为绝对黑体的辐射常数。因此,这一定律以这两位科学家的名字命名,称为“斯蒂芬-波尔兹曼定律”。
通常在计算中,由于热力学温度T值一般为百位数,(T/100)则为个位数,因此将该定律改写为如下更便于计算的公式:
式中,C0=5.669W/(m2·K4),称为“绝对黑体的辐射系数”。此式也称为斯蒂芬-波尔兹曼定律的数学表达式。
根据普朗特定律所揭示的规律,也可以求出绝对黑体的辐射力为
式(a)的积分结果为
式(b)与式(17-4)完全相同。这充分说明,无论从实验或理论都可以得出绝对黑体的辐射力与其表面热力学温度的四次方成比例这一客观规律。
四、兰贝特定律
如图17-5所示,物体的微元表面向半球空间的各方向发射辐射能。为了描述辐射能沿半球空间各方向的分布。首先介绍立体角的概念。“立体角”是球面上的给定面积a对球心所张的球面角,它的大小用该面积a除以球面半径r的平方来计算。例如,图17-5中球面上面积da与球心所张的立体角为dω=da/r2。当球面上给定面积a=r2时,则ω=r2/r2=1,即此立体角为单位立体角,用符号sr(球面度)表示。对于半球空间,由于其面积为2πr2,所以半球空间对球心的立体角ω=2πsr。其次,介绍可见面积的概念。如图17-6所示,n为微元面积dA的法线方向,p为与法线成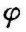 角的方向。在半球空间的不同位置上,dA的可见面积是不同的:从n方向看就有dA大;而从p方向看则为dAcos
角的方向。在半球空间的不同位置上,dA的可见面积是不同的:从n方向看就有dA大;而从p方向看则为dAcos ;如
;如 =90°,可见面积为零,即从与n成90°的方向看不见dA的存在。因此,沿p方向发射的辐射能,dA的可见面积就是其在与p垂直方向的投影面积,如图17-6所示。
=90°,可见面积为零,即从与n成90°的方向看不见dA的存在。因此,沿p方向发射的辐射能,dA的可见面积就是其在与p垂直方向的投影面积,如图17-6所示。
图17-5 微元表面dA向半球空间的辐射
引用立体角和可见面积,定向辐射强度可定义为:单位时间内与发射方向p垂直的单位可见面积在单位立体角内所发射的辐射能,用符号Ip表示,其单位为W/(m2·sr)。按定义,IP可以表达为
物体表面在半球空间各方向上,如定向辐射强度均相等,即
则该物体表面称为漫辐射表面。兰贝特指出,只有绝对黑体的表面才是漫辐射表面。因此,兰贝特定律可表述为:绝对黑体表面沿半球空间各方向上,定向辐射强度均相等。
图17-6 定向辐射强度
对于黑体,Ip=I0为定值,式(17-5)可改写为
可见,单位时间内,黑体单位表面积沿半球空间不同方向在单位立体角内所发射的辐射能是不同的:沿法线方向, =0,发射的能量值最大(即I0),随着
=0,发射的能量值最大(即I0),随着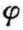 的增加,发射的能量值按余弦规律而减少;当
的增加,发射的能量值按余弦规律而减少;当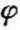 =90°时,发射的能量为零。因此,兰贝特定律又称余弦定律。(https://www.xing528.com)
=90°时,发射的能量为零。因此,兰贝特定律又称余弦定律。(https://www.xing528.com)
由式(17-7),黑体微面积dA 向半球空间发射的辐射能量dQ0,dA为
参见图17-5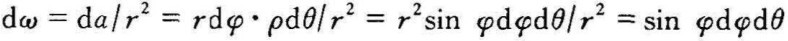 ,将这一关系代入上式,得
,将这一关系代入上式,得
于是,黑体的辐射力为
可见,黑体的辐射力E0等于其定向辐射强度I0的π倍。
对于实际物体表面,各个方向上的定向辐射强度并不是定值,工程上只是近似地认为它符合兰贝特定律,并将该辐射表面视为漫辐射表面。
下面,对绝对黑体热辐射的物理性质作一个小结:黑体辐射能量按波长分布服从普朗特定律,按空间分布服从兰贝特定律,辐射力大小由斯蒂芬-波尔兹定律确定。维恩位移定律揭示了最大单色辐射力的分布规律。
五、基尔霍夫定律
基尔霍夫在1860年确定了物体辐射力与吸收率之间的联系。这种联系可以用两个温度相等的表面之间的辐射换热推导出来。
如图17-7所示,设有两个相互平行的表面,表面1是绝对黑体,表面2是任意物体。这两个表面的温度、辐射力和吸收率分别为T0,E0,A0和T,E,A。现在来计算表面2能量的收支差额。表面2的辐射力为E,这部分能量投射至绝对黑体1上,就全部被吸收;同时表面1的辐射力E0落在表面2上时,只有一部分即AE0被吸收,其余部分(1-A)E0被反射回去,重新落在表面1上,完全被吸收。因此,表面2的辐射换热收支差额为
即使在T=T0时,两表面间的辐射换热也同样进行着,只不过体系处于热平衡罢了。这时由于q=0,于是上式变为
由于物体表面2是任意的,因此上式对任何物体1,2,3,⋯适合,由此得到以下公式:
式(17-9)即为基尔霍夫定律的数学表达式,其意义为:任何物体的辐射力与吸收率的比值恒等于同温度下绝对黑体的辐射力,而与物体的性质无关。但是应该记住,基尔霍夫定律仅仅对于温度处于平衡的热辐射是正确的。由于各种物体的吸收率永远小于1,所以在任何给定的温度下,各种物体中以绝对黑体的辐射力为最大。从基尔霍夫定律也可以得到这样的结论:物体的辐射力越大,它的吸收率也越大。
图17-7 基尔霍夫定律的推演用图
辐射换热最重要的是确定实际物体的辐射力。实际物体的辐射力E与同温度下绝对黑体的辐射力E0之比值称为“黑度”,用ε来表示
所以,黑度表征着物体辐射力接近黑体辐射力的程度,它是分析和计算辐射换热的一个重要数据。同一物体的黑度随本身的温度T和表面状态(如粗糙度、氧化程度等)而异。工程上常用材料的黑度值列于附表21中,从附表上可以看出,同一材料的黑度值变化范围很大。由于表面状态不可能得到确切描述,所以引用这类数据时需多加斟酌。
由上述已知A=E/E0,与式(17-10)比较,可得
式(17-11)表明,在温度相等的热平衡条件下,物体的黑度恒等于它的吸收率,故式(18-11)亦称为“基尔霍夫恒等式”。
同理,基尔霍夫定律也适用于单色辐射,可得出物体单色辐射力Eλ与同温度下黑体单色辐射力E0,λ之比,等于物体的单色吸收率Aλ,即
对于实际物体,其单色辐射力Eλ=f(λ,T)随波长λ和温度T的变化极为复杂,图17-8描绘了给定温度下某实际物体的Eλ与λ的关系曲线。
由图可见,相同温度下,实际物体的单色辐射力曲线的纵坐标与黑体的单色辐射力曲线的纵坐标不成比例。各种实际物体的单色辐射力Eλ随波长和温度的变化具有自己的规律。为使实际辐射表面亦能应用黑体辐射表面的有关公式,这里引入“灰体”的概念。
什么样的材料是灰体呢?如在所有波长下,物体的单色辐射力Eλ与同温度、同波长下黑体单色辐射力E0,λ之比为定值,则称该物体为“灰体”,即
式中,ελ称为灰体的单色黑度,其值与波长无关,且小于1。经验指出,大多数工程材料在热射线范围内可被视为灰体。灰体具有如下两个性质:
(1)灰体的辐射光谱是连续的,而且曲线Eλ=f(λ)与同温度下绝对黑体的光谱曲线相似,如图(17-8)所示。
(2)灰体的吸收率等于其黑度,与投射辐射无关。证明如下:
根据吸收率的定义,灰体的吸收率A等于吸收辐射与入射辐射之比,即
图17-8 辐射光谱和吸收光谱
根据灰体的性质(1),Aλ(λ,T4)=ελ(λ,T4)=ελ(T4),代入式(17-12)中,可得
由(17-12a)可知,斯蒂芬-波尔兹曼定律也适用于灰体。工程上的材料严格来说还不是灰体,只是认为接近灰体的工程材料也具有辐射力E与其表面温度T的四次方关系。于是可得
式中,C=εC0=AC0称为灰体的辐射系数,由于灰体的黑度(或吸收率)恒小于1,所以任何物体的辐射力恒小于同温度下绝对黑体的辐射力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




