受迫对流中的层流和紊流换热机理与计算方法

一、流体沿平壁流动时的对流换热

流体沿平壁流动时，速度边界层和热边界层的形成，以及它们与换热系数α的关系，在前一章已作了较为详细的介绍。由于它是受迫对流换热中最简单的一种，层流时平均换热系数的计算公式可由数学分析方法获得；紊流时平均换热系数的计算公式可由柯尔伯恩类比获得。实验表明，这些计算公式比较准确，可用于工程计算。现归纳如下。

当Rem＜5×105（层流）、Prm＝0.5～50时，对空气、水和变压器油，换热系数α的计算公式为

式中，Num和Rem中的定性温度为tm＝（tf＋t W）/2，定形尺寸为沿流动方向平壁的长度l；Prm中的定性温度也是tm。将上式写为求α的有量纲形式

可见，流体对平壁的换热系数α与流体的物性参数λ2/3，υ﹣1/6，和ρ1/3成正比，并与流速w1/2和板长l﹣1/2成正比。在工程中，如要求增强流体与平壁的对流换热，即增大α值，则应采用λ、cρ和ρ大以及υ小的流体，提高流速w，以及在平壁上开若干槽口（与流动方向垂直）使平壁由l较小的若干段所组成。

当Rem＝5×105～107处于紊流换热、Prm＝0.5～50时，对空气、水和变压器油，其换热系数可用下式来计算：

式中，Num和Rem中的定形尺寸为板长l；定性温度为tm。

二、流体在管道内换热

从流体力学我们知道，流体从管道入口进入管道后，流体流动的速度边界层厚度从零开始增长直到会合于管道中心线，流入一段距离后，流体的主流状态便消失，而管内流体全处于层流边界层或紊流边界层的流动状态。类似地，流体在管道内流动时，流体与管壁间的换热过程，管壁上的热边界层厚度从零开始增长直到会合于管道中心线，其局部换热系数αx随流入长度的增加而下降。当速度边界层和热边界层会合于管道中心线后，称流动和换热已经充分发展，此后的换热系数将保持不变。从进口到充分发展段之间的区域称为入口段。入口段的热边界层较薄，局部换热系数比充分发展段的高，且沿着主流方向逐渐降低，逐渐靠近充分发展段，局部换热系数逐渐趋于稳定。工程技术中常常利用入口段换热效果好这一特点来强化设备的换热。

由于流体的温度分布及平均温度随着离入口处的距离的增加而变化，因而不能用入口处的流体温度来表示流体在管内的温度，只能用管子进口和出口截面上的平均温度的算术平均值来表示，即

虽然光滑直管道的形状是多种多样的，但流体在管内流动的特点却变化不大。对圆管用直径d，对任意截面形状的管道用当量直径[式（15-53）]，应用相似理论指导实验，对Prf＝0.6～2500的各种流体，得出不同Ref范围的管内层流、过渡状态以及紊流换热时求α的准则方程。

1.管内层流时的准则方程

适用于Ref＝wde/υf＜2300的层流换热，即

式中：dc/l——管长对α影响的无量纲量；

μf/μW——考虑流体被管壁加热或被冷却时的不同热流方向对α影响的无量纲量。

式（16-5）不适用于过长的管子，只限用于（Ref·Prf·de/l）＞10的层流换热过程。此式的定性温度为流体的平均温度tf，但μW按壁温计算，特征长度为管径。在实际工程换热设备中，层流时的换热常常处于入口段的范围。

2.管内过渡状态时的准则方程

在Ref＝2300～104范围内，流动为过渡状态。由于整理实验数据所得的准则方程不便于计算，所以列出计算表格，见表16-1。

表16-1 计算表格

3.管内紊流时的准则方程

当Ref＝104～1.2×105时，整理大量Prf＝0.6～120的流体管内紊流换热实验数据，得出准则方程为

式中：εl——管长修正系数；

εR——弯管曲率修正系数；

εt——壁面温度与流体温度差值较大时所用的温差修正系数。对于：l/de＞50的长管道，εt＝1；直管道，εR＝1；气体被管壁冷却时，εt＝1；若流体为空气，取Prf＝0.71，则式（16-6）为

写成有量纲的形式，则式（16-7）为

式（16-8）清晰地表示了α随λf，w，de以及υf的变化关系。从流体力学可知道，流体的Re数在阻力平方区内，当流速增加1倍时，其管道的压降Δp将增加3倍，由于流速增加1倍，将使流量也增加1倍，而所消耗的泵功将增加7倍。可见，欲提高管内流体对管壁的换热系数，是必须付出代价的。

图16-1所示为不同Ref时管长修正系数εl与比值l/de间的关系曲线。当l/dc＜50时，应进行修正。当de相同时，则短管有较大的α值。

图16-1 不同Ref时εl与l/de的关系曲线

流体在弯曲的蛇形管中流动，由于扰动度较直管为大，致使换热系数增高。因此，式（16 6）中的弯管曲率修正系数可按下式计算：

对于空气

对于液体

当壁面温度t W与流体温度tf之差较大时，温差修正系数εt按下列不同情况计算：气体被加热时

气体被冷却时

液体被加热时

液体被冷却时

工程上有些流体并不是在管道内流动，如在板式换热器的板间流动进行对流换热，它也具有管内流动的特征，只不过由于板型的不同使流体的扰动情况不同。反映在准则方程式中，则为系数c、指数m及n的值因板型不同而不同。

某换热器厂制造的某型板式换热器，应用于热水对冷水的传热实验，得出了下列准则公式

式中，流体被冷却一侧的m＝0.3；流体被加热的一侧的m＝0.4。

另一换热器厂制造的某型板式换热器，应用于热水对冷水的传热实验，得出了如下准则公式

式中，流体被冷却一侧的m＝0.3；流体被加热一侧的m＝0.4。

由板间流速及流道当量直径所求得Ref＜2300时，流动已呈紊流状态，这是由于波纹板的曲折流道所形成的人工扰动所致。

例16-1 tf′＝25.3℃的水，流入l＝5m的直管，并被加热到tf″＝34.7℃，管子内径d＝20mm，水在管内的流速w＝2m/s，求换热系数。

解 直管内水的平均温度

从附表16中查得水在30℃时，λf＝0.618W/（m·K），υf＝0.805×10﹣6m2/s，Prf＝5.42。则

代入式（16-6）

由于不知壁温，又是l/d＞50的直管，因此无需修正。(www.xing528.com)

三、流体横掠圆管时的换热

燃气流过蒸汽锅炉的蒸发管、过热器管和省煤器管时，将热量传递给管内的工质。船上的各种冷却器也都制成管束而靠流体流过时进行换热。为了说明流体流过圆管时的换热特点，先来叙述流体流过单圆管时的换热规律。

1.流体横掠单管时的换热－

所谓横掠单管，就是流体沿着垂直于管子轴线的方向流过管子外表面。流体横掠单圆管时，在前滞止点＝0处被分成两股，从上、下两侧流过圆管并在圆管壁面上形成层流边界层，沿流动方向边界层厚度逐渐增大。在圆管壁＝90°附近，流体脱离壁面，边界层分离而形成旋涡，如图16-2所示。

沿圆管周边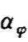/α随角变化的曲线见图16-3。当Ref＝104时，＝0处的为圆管平均换热系数α的1.6倍。由于前半部45％左右的管面受到气流的直接冲刷，以及＝0处附近的层流边界层很薄，致使圆管前半圆周的对流换热较后半圆周更为强烈。随角的增大，层流边界层发生分离形成旋涡，旋涡冲刷圆管的后半部，使得回升。

图16-2 流体横掠圆管时的流动情况

图16-3 沿圆管周边/α与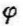角的关系曲线

综合整理空气、水和变压器油等流体横向流过金属圆导线和圆管时的大量实验数据，得出下列准则方程：

当Ref＝10～103时

当Ref＝103～2×105时寸

若流体为空气，由于Pr随温度变化不大，可近似地取Prf＝0.70，则空气横掠单管时的准则方程可化简如下：

当Ref＝10～103时

当Ref＝103～2×105时

上述方程不允许推广到非圆管，因为横掠管道的几何形状对于对流换热的影响程度较强烈。

2.流体横掠圆管束时的换热

图16-4 流体在管束间的流动情况

流体横掠管束时的换热过程远比横掠单管时复杂。管束的换热系数值，与其排列方法（即顺排还是叉排）有关，与排列的紧凑程度S1/d、S2/d有关，与横向管距S1和纵向管距S2之比有关，还与管子所在的排数即第几排有关。图16-4（a）示出流体在顺排管束间的流动情况。图16-4（b）示出流体在叉排管束间的流动情况。顺排时，除了第一排＝0的正面处受到流体的冲击以外，其余各排管子的正面与背面都处于涡流区域，受不到冲击。叉排时，各排的正面都要受到冲击。此外，叉排时流体在管间交替收缩和扩张的弯曲通道中流动，比顺排时流体在管间走廊通道的流动扰动剧烈。因此，一般来说，叉排时的换热比顺排时强。然而，也应注意到，叉排管束的阻力大于顺排，且对于需要冲刷清洗的管束，顺排有易于清洗的优点，所以，叉排、顺排的选择要全面权衡。

经过用空气、水和油类等各种流体对顺排和叉排管束进行大量实验后得知，各排的换热系数值依排序而增长。这是因为流体每流过一排管，它的扰动都要增强。由于叉排管束中的流体扰动度大于顺排管束，因此在同样的入口流速下，叉排管的平均换热系数要大。当Ret＝104时，空气流过叉排管束时的平均换热系数约为顺排管束的111％。Ref越大，二者的差值越小。这是因为当Ref较高时，流体的扰动比较激烈，不同的排列对扰动度的影响不明显。

根据大量实验数据，当Ref＝102～2×105，Prf＝0.6～500时，n排管束的准则方程如下：

顺排管束

对空气或燃气可化简为

叉排管束

对空气或燃气可化简为

式中，εn为总排数修正系数，用在少于10排的管束。实验结果表明，当多排管束时，后排管受前排管尾流的扰动作用对平均换热系数的影响主要体现在总排数在10排以内的管束，排数越少，影响越大，当总排数超过10排以上时，可以不必考虑这种扰动的影响。顺排和叉排管束的εn值列于表16-2中。

表16-2 顺排和叉排管束的εκ

定性温度除Pr W用壁温外，其余均用流体在管束中的平均温度。定性尺寸用圆管外径。流速用截面最窄处的流速，即管间流速。上列公式适用于气流垂直于管子轴线的管束，当流动方向与管轴线角度大于60°时，计算误差不超过6％，可不必修正。若角度小于60°，则应作修正。

例16-2 某锅炉叉排管束6排，管子外径d＝38mm，管束前的燃气温度t1＝700℃，管束后的燃气温度t2＝500℃，燃气在管间的流速w＝15m/s，S1＝S2。求此燃气对管束的平均换热系数值。

解查附表15得燃气平均温度tf＝（500＋700）/2＝600℃时的有关物理性质参数如下：

6排叉排管束的εn＝0.95，代入式（16-18）得

四、流体横掠其他形状换热表面时的计算公式

由于换热表面装有各种肋片，加之管子外形又有圆、扁圆和椭圆之分，因此各种带肋管束换热系数α的计算公式都不一样。 根据大量的实验，整理成图线或经验公式，供计算时使用。

1.用图线计算

图16-5为带螺旋肋片叉排管束的两组曲线，即

式中，S t＝Nu/（Re·Pr）＝α/（cppw）为斯坦顿准则。准则的定性温度为tf，定形尺寸de按下式计算：

式中，A 为带肋壁面的总面积；L 为换热壁面的纵深长度。

图16-5带螺旋肋片叉排管束求α和Cf的曲线（每米管长有346个肋片）

曲线a：S1＝49.8mm曲线b：S1＝78.4mm

可见，根据相应图线由Re值查得St·Pr2/3，便可计算出α值。同理，由Re也可查得摩擦系数Cf。如果叉排管束的几何尺寸S1，S2和肋距与图16-5所示的数据不一致，则其St·Pr2/3＝f（Re）的曲线也就不同。可见，这类图线不能推广应用。对其他各种肋形和尺寸换热壁面，其St·Pr2/3和Cf的图线可由有关手册查得。

2.横掠大块平肋套管（正三角形叉排管束）

因为这种大块平肋套管换热器制造工艺简便、紧凑度m2/m3大，即每立方米空间中具有的换热面积（平方米）较多，所以空气冷却器、加热器的换热元件广泛采用这种形式。其经验公式为

式中，l为肋高、p为肋距，定形尺寸为当量直径de。

3.横掠圆肋片圆管束（正三角形叉排管束）

当Ref＝103～2×104，其经验公式为

当Ref＝1.5×104～5×105，其经验公式为

式中，d0为圆管外径；l为肋高；p为肋距；δ为肋厚；S1为横向管距，定形尺寸为圆管外径d0。