对流换热过程的边界层分析与求解

自从1904年普朗特提出边界层概念以来，经过许多学者的努力，使得对流换热过程的分析求解有了很大的进展。如上节所述，由于边界层微分方程组得到了实质性的简化，从而使得数学分析求解较为简单。这种由边界层微分方程组求得的解，通常称为“分析解”。但是，边界层微分方程组中的方程仍为偏微分方程，因而能用其分析求解的范围很有限。这样就要求在对流换热过程的分析求解上开辟新的途径。目前应用最广泛的方法是：建立边界层动量积分方程和边界层能量积分方程，这两个方程都是常微分方程，然后对其分析求解。这种方法不需要求解偏微分方程，因而分析求解简便。这种由边界层积分方程组求得的解，与分析解比较显得有些粗糙，因而通常称为“近似解”。虽然如此，由于这种方法适用范围广，而且所得的解有足够的精确度，因而得到广泛应用。本节将主要介绍“近似解”，对“分析解”只作简要介绍。

一、边界层的基本概念

流体以某一速度和温度流过固体壁面时，由于流体有粘性，在紧贴壁面处的流速为零，其温度也等于壁温。因此在壁面的法线方向有速度梯度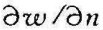/ 和温度梯度。现定义贴近壁面的具有明显速度梯度的那一层流体为速度边界层。同样，定义贴近壁面的具有明显温度梯度的那一层流体为热边界层。速度边界层与热边界层有密切的关系，而热边界层的厚薄变化直接影响换热系数α值。因此，为了说明对流换热的机理及影响α的各种因素，下面先对速度边界层和热边界层进行简要的分析。

1.速度边界层

流体在贴近壁面处形成的速度边界层，按其特征又可分为层流边界层和紊流边界层。而这些特征又影响对流换热的强度。图15-4表明了边界层在贴近平壁处的形成和发展过程。流体以流速w∞流经平壁，由于流体具有粘性，致使紧贴壁面处的流速为零，而离壁面越远的

图15-4 流体流经平板时速度边界层的形成和发展

流体速度越接近w∞。若在离平壁前缘x处用热线风速仪或激光测速仪，便可测出在壁面法线方向y上各点的流速。这一速度分布用w＝f（y）曲线表示。在w等于0.99w∞处以外的流体，可以认为已不受流体粘性的影响，称其为主流区。在w＝0.99w∞以内的流体层有明显的速度梯度，按牛顿内摩擦定律

式中：τ——粘滞力，N/m2；

μ—动力粘度，kg/（m·s）

即粘滞力与速度梯度成正比。在速度边界层内有较大的速度梯度，显然就有较大的粘滞力。由于粘滞力的牵制，在这一边界层内流体微团只能沿着壁面平行地分层流动，我们称它为层流边界层，其厚度用δ层表示。在流体力学中应用数学分析法可求得层流边界层厚度为

式中：x——以平壁入口边缘起算的距离，m；

ν——流体的运动粘度，它是流体的动力粘度μ与流体密度ρ之比，m2/s；

w∞——主流速度，m/s；

Rex——局部雷诺数，即

在x＝0处，即入口边缘处，层流边界层的厚度为零。随着x的增大，δ层增大。当x增大到某一临界值xcr时，层流边界层厚度增大到某一极限值，而使边界层失去层流的特征而转变为趋向于紊流的过渡状态。这是因为δ层越厚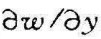，相应减小，粘滞力τ也下降。当流层中的粘滞力阻尼不了流体主流中的任何微小扰动时，则层流的特性逐渐不明显，呈现出横向脉动和旋涡的过渡状态。实验证明

也即临界雷诺数

时，层流边界层发展为过渡状态，随着x的增加，将过渡到紊流边界层。在紊流边界层内，由于紧贴壁面处那一薄层内粘滞力甚大，流体仍具有层流的特征，所以称之为粘性底层。粘性底层上方称为紊流支层，在该层内由于粘滞力较小，流动具有紊流的特征。由图15-4可见紊流边界层的厚度δ紊是由紊流支层和粘性底层所构成。根据计算可得紊流边界层的厚度为

此式表明在平壁的x处，w∞越大υ越小，δ紊将越薄。同理也可看出，对w∞与ν一定的流体，x越大，δ紊越厚。也可求得粘性底层的厚度为

由式（15-11）及式（15-14）可见，流体的主流速度w∞越大，层流边界层厚度δ层以及粘性底层的厚度δ底越薄；x增大时，δ层随x0.5成正比增加，而δ底则随x0.1成正比增加，这表明当x增大时，δ底增加很少。

上述判别层流边界层过渡到紊流边界层的临界雷诺数Recr＝5.0×105，只适用于流体流经平壁的流动情况。

对于在管内的流体运动，取管内临界雷诺数Recr＝wd/ν＝2300。w为管内平均流速，d为管子内径。

综上所述，流体掠过平壁，在壁面附近形成的层流边界层沿流向x而增厚。当流体进入过渡段时，边界层虽然增厚，但具有层流性质的边界层逐渐变薄。当流体进入紊流边界层段时，粘性底层厚度δ底，随着x的增加按式（15-14）的规律变化，即按δ底与x1/10的关系变化。

图15-4给出了边界层速度分布曲线的形状。对层流时，其速度分布为抛物线形，而紊流时，速度在粘性底层部分变化比较剧烈，而在底层以外的区域，速度变化趋于平缓。

从以上讨论，可以得出速度边界层的几个重要特性：

（1）边界层厚度δ远远小于壁面的尺寸l；

（2）边界层内壁面法线方向的速度变化非常剧烈；

（3）边界层流动状态分为层流与紊流，而紊流边界层内紧靠壁面处保持层流性质，称为粘性底层；

（4）流场可划分为主流区和边界层区，只有在边界层区内才体现流体粘性的影响，其影响的程度和边界层流动状态有关，当Re数很小时，粘性力占优势，可以忽略惯性力；当Re数很大时，边界层为紊流状态，除粘性底层外，惯性力起主导作用，可以忽略粘性力；当Re数处于以上两种情况之间时，惯性力和粘性力的数量级是相当的。

2.热边界层

流体沿平壁流动，主流温度为tf的流体与壁温为t W的平壁之间进行对流换热时，流体在壁面附近的一薄层内具有明显的温度梯度，该薄层称为热边界层，其厚度用δt表示。图15-5为该换热过程中，紊流边界层内x 处的热边界层示意图。

在y＝0处，流体温度等于壁温t W，以t W为基准的流体的过余温度θ0＝t－t W＝0。在y ＝δt的热边界层的界面上，流体的过余温度θδ＝tδ－t W＝0.99（tf－t W），即tδ＝0.99（tf－t W）＋t W，可以认为已接近主流温度tf。按紊流边界层的温度分布t＝f（y）可以看出：在粘性底层厚度δ底内具有较大的温度梯度；在紊流支层内除流体的导热作用以外，由于流体的旋涡运动使流体的温度梯度变小。 可见热边界层与速度边界层有密切关系，也就是说流体在壁面法线方向y 上的温度分布t＝f（y）与其速度分布w ＝f（y）有关，但并不完全相同。因此，速度边界层的厚度δ与热边界层的厚度δt有关，一般来说并不相等。

图15-5 热边界层示意图

根据流体掠过平壁的对流换热过程的数学分析可得出

式中，ν/a ＝Pr，Pr 称普朗特数，它是运动粘度与导温系数之比。运动粘度是动量或速度的扩散率，导温系数是热量或温度的扩散率。二者之比是衡量速度分布w ＝f（y）和过余温度分布θ＝f（y）存在何种关系的指标。

显然按式（15-15），若Pr＝ν/a ＝1，则δt＝δ层，表明这两条曲线是在同一界面上达到0.99 （tf－t W）和0.99W ∞的。若Pr＞1，则δ层＞δt。若Pr ＜1，则δ层＜δt。

Pr 数是无因次量，它与流体的物理性质及温度有关。Pr 数在有关的传热学书中皆可查得。图15-6为不同流体的Pr 数值范围。

对于180℃的饱和水，Pr＝1，则其δt＝δ层。

图15-6 不同流体的Pr 值范围

对于空气Pr＝0.71，则δt＝1.15δ层。

对80℃的润滑油Pr＝490，则δt＝0.084δ层，表明δ层远较δt厚。

对于液态金属，式（15-15）不适用，由数学分析可得出

对于Pr＝0.01的液态金属，δ层＝0.164δt。可见液态金属的热边界层，远厚于层流边界层的厚度。

用式（15-11）、（15-12）、（15-14）或式（15-15）可计算出δ和δt值，但都只有几毫米。当流速越大时，其δ1越薄，对于温差（tf－t W）一定的对流换热过程来说，热边界层内的温度梯度也越大。离平壁前缘x处的对流换热热流密度qx必定随该处的温度梯度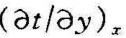增大而增大。

热边界层的边界线将流体的温度场划分为两个区域，只有在热边界层中才有温度变化，而在热边界层以外可以认为温度梯度为零，当做等温流动区。

速度边界层和热边界层的状态决定了边界层热量传递过程。对于层流，壁面法线方向热量传递靠导热方式，边界层内温度分布为抛物线；对于紊流，粘性底层的热量传递靠导热，而在底层以外的紊流支层，除导热方式外，主要靠速度脉动引起的对流混合作用。对于导热系数不高的流体，由于热对流方式传递热量比导热方式强，所以紊流换热热阻将主要取决于粘性底层的导热过程，边界层的温度梯度在粘性底层最大，而在紊流支层中变化平缓。

二、边界层对流换热微分方程组及其分析求解简介

前已指出，分析求解描述对流换热过程的对流换热微分方程组式（15-9）是非常困难的。如果用边界层的概念，对动量微分方程和能量微分方程进行数量级分析，使之得以简化，求解就方便了。

所谓数量级分析，是指通过比较方程中各量或各项量级的相对大小，从方程中舍去那些量级极小的项，而保留量级较大的项，这样，方程就可以被大大地简化。在流体力学中，已经将动量微分方程作数量级分析和简化，得到了普朗特边界层微分方程。利用同样的方法，也可以将能量微分方程加以简化。

在此，仅以常物性、不可压缩流体沿平壁稳定层流边界层流动为例，列出其边界层对流换热微分方程组及其分析解，具体的数量级分析、简化过程和分析求解过程可分别参阅有关文献。

常物性、不可压缩流体沿平壁层流边界层稳定流动时，边界层对流换热微分方程组为

连续性方程

动量方程

能量方程

换热方程

设来流的速度均匀、温度均匀，分别为w∞和tf，平壁壁面温度为常数t W，则边界条件为

由于设定为常物性，方程组中的热物性参数υ、a和λ均为常数，与温度无关，因此可由连续性方程式（15-17）和动量方程式（15-18）先求解速度场，在此基础上由能量方程式（15-19）解得温度场。从物理意义上讲，在常物性的条件下，对流换热过程的热传递并不影响流体的速度场；反之，由式（15-19）可以看出，由于能量方程中含有wx和wy，因此流体的速度场影响流体的温度场。最后将求得的温度场表达式代入换热方程式（15-20），可求得局部换热系数αx。

求解这个微分方程组，可得速度边界层厚度δ、壁面上的粘性切应力τW和摩擦系数cf、壁面的局部换热系数αx和无量纲准则方程式的分析解为

式中，为局部努塞尔数，无量纲，其大小反映了局部对流换热的强度。

三、边界层对流换热积分方程组及其分析求解

边界层对流换热问题也可以由建立边界层对流换热积分方程组的途径求解。这比建立边界层对流换热微分方程组求解的途径更加简捷和易于理解。

这里仍以常物性、不可压缩流体沿平壁稳定层流边界层流动为例，介绍其边界层动量积分方程和边界层能量积分方程，说明其分析求解的大致步骤。(www.xing528.com)

1.边界层动量积分方程及其分析求解

根据流体力学，对于沿平壁流动，其边界层动量积分方程为

如图15-7所示，在沿平壁的速度边界层中取出一高度为δ、横向为dx、宽度为1单位长度的控制体。这一控制体与微元体的区别在于：后者在高度方向（y方向）为无限小，而前者在高度方向为有限值——即速度边界层的厚度为δ。边界层动量积分方程就是对这一控制体应用质量守恒定律和动量定律而推导出来的。因此，它只表述了在所取控制体的总体上满足动量定律，而边界层动量微分方程则表述了对每一流体微团均满足动量定律。可见，边界层动量积分方程显得粗糙一些。但它只包括一个自变量x，因而是一个常微分方程，较之包括两个自变量x，y的偏微分方程求解要简单得多。

图15-7 推导边界层动量积分方程用控制体

在常物性条件下，用边界层动量积分方程可求解出速度边界层厚度δ和摩擦系数cf。分析求解步骤大致如下：给定边界层内速度wx沿y方向的分布表达式，如采用

式中，系数a0，a1，a2，a3由边界条件和边界层特点确定，即

于是，速度分布表达式为

将上式代入边界层动量积分方程式（15-27），且考虑到

可得

因为x＝0时δ＝0，对上式积分

可得

于是τW和cf分别为

这就是δ和cf的所谓近似解，与式（15-22）和式（15-24）所示分析解比较，是很接近的。速度边界层近似解的精确度在很大程度上取决于所给定的速度分布表达式的合理性。

2.边界层能量积分方程及其分析求解

对于沿平壁流动，其边界层能量积分方程为

这一方程的推导与边界层动量积分方程的推导是相类似的，即在沿平壁流动的热边界层中取出一高度为δt（热边界层厚度）、横向为dx、宽度为1单位长度的控制体。对这一控制体应用质量守恒定律和能量守恒定律，且略去沿x方向的导热，就可推导出边界层能量积分方程。上式中的wx是已知量，因为速度场已解出。同样，这个方程也只包括一个自变量x，是一个常微分方程。

边界层能量积分方程的分析求解是在速度场已解出的基础上进行的，其步骤大致如下：与解动量积分方程相类似，也是给定热边界层内温度t沿y方向的分布表达式，如采用

式中，系数b0，b1，b2，b3由下列条件确定，即

于是，温度分布表达式为

取以t W为基准的过余温度θ＝t－t W，则上式可改写为

能量积分方程式（15-31）用过余温度表示为

令ξ＝δt/δ，它表示热边界层厚度与速度边界层厚度之比。当ξ＜1，即热边界层在速度边界层之内时，可将速度分布式（15-28）和温度分布式（15-32）代入上式直接进行运算，可得

因为给定ξ＜1，所以（1－ξ2/14）≈1，于是

于是

将速度边界层δ的计算式（15-29）代入上式，并经运算整理，可得

式（15-34）是一个关于（ξ3）的一阶线性非齐次常微分方程，在边界条件

时，其解为

于是

将速度边界层厚度δ式（15-21）代入上式，可得

3.换热系数的求解

根据式（15-5），局部换热系数αx为

将温度分布式（15-32）代入上式，可得

再将式（15-36）代入式（15-37），可得

这是由三个无量纲数Rex，Pr和Nux组成的无量纲方程。

根据式（15-4），长度为l的平壁，平均换热系数α为

根据给定条件

可得

式中，αl为l处的局部换热系数，可见长l的平壁的平均换热系数α为αl的二倍。

将上式写为无量纲形式

式中，Nu＝αl/λ为平均努塞尔数；Re＝Rel＝w∞l/υ为雷诺数；Pr＝ν/a为普朗特数。

无量纲数Nu，Re所包含的几何尺寸称为定形尺寸，对沿平壁流动取其长度l为定形尺寸。

Nu，Re和Pr中所包含的流体热物性λ，υ，α用边界层的平均温度tm＝（t W＋tf）/2计算。

由式（15-35）可以看出：当Pr＝1时，δt≈δ，即对普朗特数等于1的流体，热边界层厚度与速度边界层厚度可以认为是相等的；当Pr＞1时，δt＜δ；当Pr＜1时，δt＞δ。

式（15-39）是在给定条件ξ＝δt/δ＜1的条件下推导出来的，因此严格来说，该式仅适用于Pr＞1的流体。但对Pr接近于1的气体，因为（1－ξ2/14）＝（1－1/14）＝0.929≈1，所以这个式子还是适用的。实验数据表明，在Re＜2×105的层流范围内，由边界层积分方程组分析解得的近似解[式（15-39）]有足够的精确度。

例15-1 空气在27℃和0.1013MPa压力下以每秒10m的速度沿平板流动，试计算离板前缘0.3m处的速度边界层厚度δ和热边界层厚度δt。

解由附表14，按300K的空气物性参数查得

算得

按公式（15-29）得

由公式（15-35）算得

计算表明层流边界层厚度δ层与热边界层厚度δt只有几毫米，远较平板的长度要小得多。

例15-2 求上题x＝1m处的边界层厚度。

解

Rex＞Recr，流体已进入紊流边界层，所以根据式（15-12），得

又由式（15-14）

可见，粘性底层在紊流边界层中只是很薄的一层。

例15-3 如例15-1中所给定的条件，求x＝30cm处的局部换热系数αx以及从x＝0到x＝30cm处的平均换热系数值α。

解 按公式（15-38）可求得

按公式（15-39）可求得

总之，以边界层概念为基础的对流换热过程的分析求解，对于边界层很薄的层流范围内是有效的。在一定来流速度下，对于粘性小的流体是属于高雷诺数的流动。由流体力学可知，高雷诺数流动具有边界层很薄的特点，而工程常用流体，如空气和水粘性很小，因而分析求解具有工程实用意义。但当不具备这些条件时，如绕圆柱流动发生边界层分离后的对流换热过程，边界层的微分方程组和积分方程组已不再适用，因而其分析求解失效。

近年来随着电子计算机和计算方法的迅速发展，一些稍为复杂的工程实际问题，也可用数值解法来求解，但数值解法还尚未完善，目前只能用作预测计算。而大多数工程问题，如流体横掠单管和管束的对流换热问题还无法求得数学分析解。因此，目前工程上常用的还是基于实验数据所得出的无量纲准则经验公式。