如何分析和求解对流换热系数α

对流换热是流体的热对流与热传导联合作用的结果。对流换热的计算采用牛顿冷却公式

式中，q为对流换热的热流密度。

一、对流换热系数

改写式（15-1），可得

式中，Δt＝|t W－tf|为固体壁面温度t W与流体温度tf之间温差的绝对值；热流密度q约定恒取正值；α为对流换热系数，简称换热系数，其单位为W/（m2·K）。由上式可见，换热系数α在数值上等于流体与壁面温差为1K时，单位壁面面积与流体之间交换的热流量，且恒取正值。

实际上，影响对流换热过程的因素很多。计算热流密度q的牛顿冷却公式（15-1）并没有给出q与影响因素之间的具体关系。从式（15-1）改写而得的式（15-2）也仅仅给出了换热系数α的定义。其实，牛顿冷却公式只是将对流换热的复杂性转移到换热系数α上去了。因此，研究对流换热就要分析影响换热系数α的各种因素以及求解换热系数α的各种方法。

二、局部换热系数和平均换热系数

在一般情况下，沿着流体的流动方向，换热系数是变化的。为了描述换热系数沿流动方向的变化规律，引进了局部换热系数的概念。而从工程应用的观点，为了计算整个换热壁面与流体之间的热流量，又引进了平均换热系数的概念。

1.局部换热系数

根据换热系数的定义式（15-2），局部换热系数αx可定义为

式中，qx为换热壁面上x处的局部热流密度；Δtx＝|（t W－tf）x|为该处的局部温差；αx则为该处的局部换热系数。

2.平均换热系数

由式（15-2），平均换热系数α可定义为式中，为平均热流密度，它等于整个换热壁面的热流量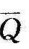除以其换热面积A，即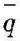＝/A；，为整个换热壁面与流体之间的平均温差。在传热学中，平均温差的计算方法有很多，因此由式（15-4）求平均换热系数α时，应注意的计算方法。为了简便，在不致混淆时，可用q，Δt和α分别表示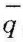，和。

三、换热微分方程

当流体在壁面上流动时，流体速度由于粘性的作用，在靠近壁面的地方逐渐降低。在贴壁面处流体的速度为零，无相对于壁面的流动，对流换热量只能以导热方式通过这一极薄的贴壁流体层，其局部热流密度qx按傅里叶定律为

另一方面，局部热流密度qx按牛顿冷却公式为

以上两式应相等，于是可得

此式描述了对流换热系数与流体温度场的关系，称为“换热微分方程”。

若已知流体的温度tf、流体的导热系数λ、壁温t W和流体的温度场，则由换热微分方程可求得局部换热系数αx。

局部换热系数αx在整个换热面的积分平均值即是该换热面的平均换热系数α。

四、影响换热系数的因素

由于对流换热是运动着的流体与固体壁面之间热传递，因而除两者的温差之外，一切有关流体流动和固体壁面的种种因素，也都将影响换热系数的大小。所以，换热系数α的大小不仅与流体的热物性有关，还与流体流动的动力因素、流体流动的状态、换热壁面的热状态以及换热壁面的几何因素等有关。现分述如下：

1.流体流动的动力因素

流体流动的动力因素是指流体运动产生的原因。

对流换热按流体流动的动力因素可分为强迫对流和自然对流两大类。

强迫对流是指由于风机或水泵等机械设备所产生的外力迫使流体相对于壁面而产生的运动；自然对流则由流体冷、热各部分的密度差产生的浮升力而引起。强迫对流时，整个流体有整齐的宏观运动，因而流体的流速将对换热系数α的大小产生很大的影响。而自然对流时，流体内部不存在整齐的宏观运动，因而浮升力的大小则是影响换热系数α大小的主要因素。

2.流体流动的状态

流体流动的状态是指流动的形态或结构。(www.xing528.com)

由流体力学可知，流动状态有层流、紊流以及处于两者之间的过渡状态。层流时，由于流体微团平行于壁面有规则地成层状运动，没有横向脉动，因而沿壁面法线方向的热传递只能依靠分子的导热。而紊流时，流体微团除沿主流方向运动外，还存在强烈的横向脉动，因而沿壁面法线方向的热传递不仅依靠分子的导热，而且还依靠流体微团的横向脉动，并且以后者为主。由此可见，热传递在层流和紊流中的机理是不同的。显然，流动状态也是影响换热系数α大小的主要因素。

3.流体的热物性

对流换热是流体内部导热和流体微团传递能量的复合过程。因此，流体本身的热物性对换热系数α的大小有很大的影响。影响α的流体热物性参数主要有：导热系数λ、比热容c、动力粘度μ和密度ρ等。

4.换热壁面的热状态

换热壁面的热状态是指壁温t W的大小，它对换热系数α的影响，可用下面两种情况予以说明：

（1）有相变：当壁温t W明显高于周围液体的饱和温度ts时，壁面上形成大量气泡而发生汽化沸腾现象。这是有相变的对流换热过程。有相变时，传递的热量包含了潜热，而且气泡的运动对液体产生强烈的扰动。因此，对流换热的机理则更为复杂。与无相变时比较，换热系数α要大得多。

（2）无相变：如壁温t W与流体温度tf相差甚大，则要考虑大温差所引起的流体内部各部分热物性参数的不同对换热系数α的影响。

5.换热壁面的几何因素

换热壁面的形状、大小以及相对于流动方向的位置等均为换热壁面的几何因素。壁面的几何因素不同，流体的流动情况也随之变化，从而引起换热系数α的变化。例如，流体横掠过不同断面或不同直径的管道时就会具有不同的换热系数α。即使流体流过同样断面和大小的管道，当流动方向与管轴线夹角不同时，换热系数α也会不同。

五、确定对流换热系数α的方法

到目前为止，确定对流换热系数α的方法主要有三种，即数学分析法、实验法和类比法。但由于对流换热过程的复杂性，使得这三种方法各有其优缺点和适用范围，不能依靠一种方法去求解各种类型的对流换热问题。下面用方框图分别介绍这三种方法及其特点。

1.数学分析法

应用质量守恒、能量守恒、动量守恒等基本物理规律描述一般的对流换热现象，再加上某一对流换热现象所具有的单值性条件，便可建立起某一个对流换热过程的物理模型，再应用数学方法建立起数学模型，就可以求得换热系数α的解。

数学分析法求解的步骤和特点用方框图表示，如图15-1所示。

图15-1 数学分析方法求解的步骤和特点

由于数学上的困难，目前还只能得到个别简单的对流换热问题的精确解。一般情况下，从对流换热过程的数学模型直接求得α的精确解是非常困难的，甚至是不可能的，因而，只能通过各种途径求其近似解。目前用数学分析法求近似解α主要有以下两种途径：一是引入边界层的概念，把对流换热过程的数学模型作适当的、合理的简化，以求得α的边界层分析解；二是将对流换热过程的微分方程转换为流场内各节点的离散方程，利用计算机和各种计算方法，求得α的数值解。对流换热的数值求解方法在近20年内得到了迅速发展，并将会日益显示出其重要的作用。

2.实验法

实验法分为两种：经验法和半经验法。经验法是利用测出的某对流换热过程中的Q，A以及tf，t W，按照牛顿冷却公式计算出α值，然后根据在某一实验范围内获得的一系列α值，将其整理成经验公式供工程计算时使用。这种方法获得的α值，其准确度决定于测量的准确性。归纳起来影响实验准确性的四种基本类型的误差为：仪器测量误差，人为误差，使用误差及计算误差。因此必须选用合适的并经过校正的仪表，防止偏视等人为误差，同时要正确选择有效数字进行计算。用经验法求α值是比较准确的，其缺点是它所求的α值不能推广应用于实验以外的任何别的对流换热过程。

半经验法是根据描述对流换热现象的物理模型，用相似理论找到判别一组相似的对流换热现象所具有的必要和充分条件，应用大量实验数据整理出适用于某一实验范围内求α的无因次方程，也称准则形式的经验公式或准则方程。

这一半经验法的求解步骤的特点用方框图表示，如图15-2所示。

图15-2 半经验法的求解步骤

用量纲理论也能导出具有一定物理意义的各种相似准则，它们在量纲理论中被称为无量纲量，也可由实验来确定各无量纲量之间的关系方程。本教材对量纲理论不作介绍。

3.热量传递和动量传递的类比法

类比法既可用来求解层流换热问题，也可用于求解紊流换热问题，它是由雷诺、普朗特、卡门及马蒂内里等人先后提出并逐步完善起来的一种方法。类比法求解的基本思想是认为对流换热过程中热量传递和动量传递是类同的，并在提出了一系列的假设后，用数学关系式将两个传递现象联系起来，然后，由流体流动的阻力规律来求解对流换热规律。相对比较而言，流体流动的阻力规律无论从理论分析还是通过实验测试，都要比对流换热规律容易获得。因此，尽管类比法比较粗糙，但目前仍然是求解对流换热问题（尤其是较复杂的紊流对流换热问题）的一种简便的、有效的方法。

类比法的求解步骤和特点用方框图表示，如图15-3所示。

图15-3 类比法的求解步骤

本章将在第三、四节中分别介绍对流换热过程的边界层分析求解和实验求解。对流换热过程的类比求解请参阅有关文献。