傅里叶定律和导热系数初探

一、温度场和温度梯度

前一章已经指出，热量传递现象只有在物体或空间内部各点温度不同的条件下才能发生。而且研究热传递过程首先要研究热传递系统内部温度的分布规律。一般情况下，物体内部的温度分布既随空间变化，也随时间变化，是空间坐标和时间的函数，即

式（14-1）是温度场最一般形式的数学描述。因此，温度场是各时刻物体中各点温度分布的总称。

温度场按物体中各点的温度是否随时间而变化分为非稳态温度场（随时间变化）和稳态温度场（不随时间变化）。例如，当柴油机在起动或停机等变工况下运行时，活塞受燃气温度影响，其温度分布不仅与坐标位置有关，而且随时间变化，这时活塞内部温度场是非稳态温度场。但当柴油机运行工况不变时，高温燃气和进入气缸的新鲜空气相接触的气缸内壁，温度是周期性变化的。但是由于周期很短，其温度的波动仅在一薄层内；而与冷却水接触的气缸外壁，温度是稳定不变的，因而整个气缸壁内部的温度可以当做稳态温度场来分析研究。图14-1表示某一瞬时活塞内部的温度分布和气缸内部的稳态温度场。

图14-1 活塞内部和气缸壁的温度分布

温度场中，同一瞬时温度相等的点连成的面称为等温面。等温面与任一平面的交线为等温线。等温线与另一条温度不同的等温线是不可能相交的，它只能是封闭曲线或者终止于物体的边界面上。在图14-1（a）中微元面积dA处于温度为t的等温面上，通过dA的热流量必定与温度为t等温面垂直，即方向为n，并向着温度较t为低的方向传递。可见热流线是与等温线相垂直的。在温度场中，温度在空间上改变的大小程度用温度梯度grad t表示。它是在等温面法线方向n上单位长度的温度增量，它是一个矢量，其数学表达式为

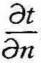表示温度在法线方向n上的导数，指向温度增大的方向为正。热传递的方向是由高温向低温，可见热流的方向与温度梯度方向相反。

二、傅里叶定律(www.xing528.com)

傅里叶在研究固体导热现象时，确定了导热所传递的热流量Q与温度梯度的绝对值和垂直于热流的截面积A成正比。由于热流的方向与温度梯度的方向相反，则

式中，λ为导热系数；Q/A为通过单位面积的热流量，称为热流密度，用q表示，则式（14-3）可写为

此即傅里叶导热定律的数学表达式。

三、导热系数

导热系数λ表明物体导热能力的程度。将式（14-4）改写为下式

由上式可以看出，导热系数是在单位温度梯度作用下物体内部所传导的热流密度值。不同物质λ值差异很大。以物质的种类来区分，λ值的大小以金属为最大，非金属固体次之，液体更次之，而以气体为最小。各种物质的λ值又都是温度的函数，有些物质的λ值随温度上升而增大，有些物质的λ值却随温度的上升而下降。多孔性物质的λ值是固体与空隙内气体λ值的组合值，因此与其密度ρ有关。例如冰的λ值为2.22W/（m·K），空气的λ值为0.024W/（m·K），而密度ρ＝50～250kg/m3的雪或霜，其λ值为0.03～0.175W/（m·K），紫铜是好的导热材料，其λ值为395W/（m·K），用作冰箱的蒸发器管。以氟利昂11作发泡剂的聚氨基甲酸乙酯（ρ＝147kg/m3），其λ值为0.0121W/（m·K），是作为冰箱箱体隔热的好材料。

大多数建筑用材和隔热的热绝缘材料的气隙或小孔是对外开口的，很易因毛细管作用而吸湿受潮。在小孔中吸有水分后，其导热系数激剧增大。这是因为水分的质传递方向与导热方向一致的缘故。例如，干燥砖的λ＝0.349W/（m·K），水的λ＝0.58W/（m·K），而湿砖的λ＝1.05W/（m·K）。工程上用的各种材料的导热系数值都是通过实验确定的，可查有关手册和本书附表。