双级活塞式压缩机的工作原理

图9-5为双级活塞式压缩机的简图，空气经低压缸压缩，压力由初压p1提高至p2（一般在0.6MPa左右），然后流入中间冷却器，再经高压缸压缩到需要的压力p3，最后充入空气瓶中。

图9-6为双级活塞式理想压缩机的p-V图。图中0—1为低压缸吸气过程；1—2为低压缸多变压缩过程；2—5为低压缸排气过程，排气后在中间冷却器中定压冷却到常温，使t2＝t1，比体积从原来的υ2缩小为υ2，V2＝mυ2；5—2′为高压缸的吸气过程；2′—3′为高压缸的多变压缩过程；3′—4 为高压缸排气过程。低压缸的示功图可用01250表示，完成一个工作过程（活塞往复一次）所消耗的机械功可用面积01250表示；高压缸的示功图可用52′3′45表示，完成一个工作过程所消耗的机械功可用面积52′3′45 表示。双级活塞式理想压缩机完成一个工作过程所消耗的机械功为低压缸与高压缸消耗的机械功之和，在p-V图上即面积0122′3′40。

图9-5 双级活塞式压缩机简图

图9-6双级活塞式压缩机的p-V

为了将空气从压力p1压缩到p3，如果用单级压缩机，所需要的机械功为面积012340，而采用中间冷却的两级压缩机所消耗的机械功则要比单级小，相差的值为面积233′2′2。空气经低压缸压缩后，再经过中间冷却器被冷却到常温，然后进入高压缸中压缩，压缩终点的温度与低压缸压缩终点温度相差不多，从而保证了气缸的良好润滑条件。

下面讨论双级活塞式压缩机耗功的计算和最佳增压比的确定。

在双级压缩机中，压缩1kg气体所消耗的机械功为低压缸与高压缸所消耗的机械功之和，对于多变压缩过程来说，它的值为

如果中间冷却器能使气体得到最有效的冷却，气体的最低温度能够达到T2′＝T1，则p1υ1＝p2υ2代入上式得

式中：p1、υ1——分别为低压缸吸入气体的压力和比体积；

p2、υ2——分别为低压缸排出气体的压力（也是高压缸的吸入压力）和比体积；

υ2——高压缸吸入气体的比体积；

p3——高压缸排出压力；

n——多变指数。

从上式可以看出，活塞往复一次，双级压缩中间冷却的理想压缩机所消耗的单位质量机械功由p1，υ1，p3，n和p2来确定。当p1，υ1，p3和n给定时，wc，n还与p2有关。可见，在双级压缩机中，当选择不同的低压缸排出压力时，所消耗的机械功也随之变化。求w C，n对p2的偏导数、导数并使它等于零，可得wc，n最小值时的p2值，即

因此

或

上式两边同开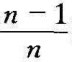次方，得

或(www.xing528.com)

式中，p2/p1和p3/p2分别为第一级和第二级的增压比。

式（9-11）表明，要使压缩机所消耗的机械功达到最小值，第一级和第二级的增压比应该相同。这个增压比称为最佳增压比。

如果分成m级压缩，各级压力设为p1，p2，p3，⋯，pm，pm＋1，则压缩机消耗的总功最小时，各中间压力应满足

这时，各级的增压比β相同，且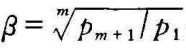。若每级中间冷却器都可将气体冷却到初始温度T1时，则各级压缩机需功相同，每一级都为

因此，选择最佳增压比不仅可以省功，而且还可以使各缸的负荷分配均匀，各缸压缩终点温度相等以及各缸的散热量相等（参见图9-7）。

例9-1 某两级压缩、中间冷却的活塞式压缩机。每小时吸入p1＝0.1MPa，t1＝17℃的空气108.5kg，可逆多变压缩到p3＝6MPa。设各级多变指数为1.2，试分析这个装置的工作情况，并与单级多变压缩（n＝1.2）至同样增压比时的情况相比较。

解 如图9-6、9-7所示，单级多变压缩时排气温度为

在活塞式压缩机中，空气的终温升高到300℃是不允许的，这将使润滑油变质而不能保证润滑。

单级压缩时压缩机所消耗的功率为

按压缩机耗功量最小的原理，确定两级压缩、中间冷却各级的最佳增压比为

即

在中间冷却器中，空气的温度降低到初温，即T2′＝T1，故各级的排气温度为

即

图9-7 双级压缩中间冷却的T-s图

两级压缩时压缩机消耗的总功率为

显然，多级压缩、中间冷却使压缩终温降低，消耗功率减小。