理想气体混合物的分体积定律及推导

一、道尔顿分压定律

理想气体混合物由若干不同理想气体所组成，各组成气体的温度都相等，且等于混合气体的温度，其所占体积也都相等，都等于混合气体的总体积。

令各组成气体处在混合气体温度T下，并单独占据整个体积V，这时作用于容器壁的压力pi称为第i种组成气体的分压力，如图7-1（b）所示。

图7-1 混合气体分压力示意图

理想气体混合物的压力等于各组成气体分压力的总和，这被称为道尔顿分压定律，即

式中：p——理想混合气体的压力；

p1，p2，⋯pn——各组成气体的分压力。

二、分体积定律

各组成气体处于混合气体的压力p和温度T时所单独占据的体积Vi称为第i种组成气体的分体积，如图7-1（c）所示。

理想气体混合物的总体积等于各组成气体分体积的总和，称为分体积定律，也称为亚美格定律，即

此定律可由理想气体状态方程和道尔顿分压定律推导出来。

三、理想混合气体的分数

如已知理想混合气体是由几种理想气体组成，其中任一种组成气体的质量为mi,分体积为Vi，千摩尔数为ni（i＝1，2，⋯，n）则理想混合气体的分数可分别表示如下。

1.质量分数

理想混合气体的总质量m，必等于各组成气体质量之和，即

上式两边同除以mi，则wi＝mi/m称为第i种组成气体的质量分数，且

即各组成气体的质量分数之和等于1。

2.体积分数

第i种组成气体的分体积与理想混合气体的总体积之比称为该组成气体的体积分数，以符号表示，即

根据式（7-2），可得

即组成气体的体积分数之和等于1。

如已知理想混合气体的压力和第i种组成气体的体积分数，由状态方程可得

p Vi＝piV

反之(www.xing528.com)

如已知第i种组成气体的分压力pi和理想混合气体的压力p，则可求得该组成气体的体积分数，即

3.摩尔分数

根据阿佛加德罗定律，任何物质1kmol的分子数目为6.023×1026，所以气体的千摩尔数可表示分子数目，而与气体的种类无关。由多种互不发生化学反应的气体组成的混合气体，其分子总数目等于各组成气体的分子数目之和。因此，混合气体的千摩尔数n可定义为各组成气体的千摩尔数之和，即

上式两边同除以n，则xi＝ni/n称为第i种组成气体的摩尔分数，且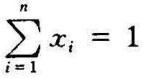，即各组成气体摩尔分数之和等于1。可以证明摩尔分数与体积分数在数值上相等，即所以，通常使用的表示理想混合气体成分的方法，从物理意义来看有三种，从数值上来看只有两种。

三、理想混合气体的千摩尔质量及气体常数

为了将单一分子气体的状态方程pυ＝RT推广应用于理想混合气体，可将其设想为单一分子组成的气体。这种假想的单一分子气体的总质量和千摩尔数与理想混合气体的总质量m和千摩尔数n分别相等，其千摩尔质量

可作理想混合气体的折合千摩尔质量。于是，理想混合气体的气体常数为

四、理想混合气体的比热容、热力学能、焓和熵

1.比热容

根据比热容的定义，如已知各组成气体的质量分数wi及质量比热容ci，则理想混合气体的质量比热容

如已知各组成气体的体积分数及体积比热容c′i，则理想混合气体的体积比热容

2.热力学能、焓和熵

因为在理想混合气体内，任一种组成气体的分子运动均不受其余组成气体的影响，所以理想混合气体的热力学能为各组成气体热力学能之和，即

同理，理想混合气体的焓和比焓分别为

同理，理想混合气体的熵也是各组成气体熵之和，即

但是，组成气体的比熵不仅与温度有关，而且还与压力有关。因为温度为T的组成气体单独存在于体积V中，其分压力为pi，所以计算组成气体比熵时应采用其分压力pi，而不是理想混合气体的压力p。因此，理想混合气体比熵的变化量由式（5－25b），可写为

例7-1 某船烟囱每秒排出绝对压力为0.11MPa，300℃的烟气60m3，由烟气分析器测得烟气的摩尔分数为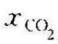＝0.104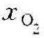，＝0.052，＝0.099，＝0.745，试求每秒排出烟气的质量及各组成气体的质量。

解 先求出烟气的千摩尔质量和气体常数，即

每秒排出烟气的质量为

为求得烟气中各组成气体的质量，将摩尔分数换算为质量分数，即

得

于是，各组成气体的质量为