理想气体热力过程的图示综合分析

多变过程在p-υ图和T-s图上的曲线形状和位置，依据多变指数的数值而定。现分别画出上述四个基本热力过程，如图5-5和图5-6所示。可观察到不同n值的多变过程在参数坐标图上的相对位置，并可分析各过程中状态参数的变化规律，还能定性地确定各过程中的能量转换关系。为了便于分析，先将多变过程曲线在坐标图上的斜率导出。

多变过程在p-υ图上的斜率

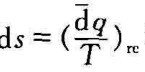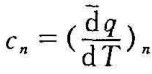由和可得

所以，多变过程在T-s图上的斜率为

图5-5多变过程在p-υ图上的表示

图5-6多变过程在T-s图上的表示

在p-υ图上，在压力和比体积相同时，绝热线斜率的绝对值总是大于定温线斜率的绝对值，即绝热线要比定温线为陡；在T-s图上，同一温度下定容线比定压线的斜率大，即定容线要比定压线陡。

综观各热力过程曲线可知，在p-υ图和T-s图上，各过程的n值是沿顺时针方向逐渐增大的。利用此规律，即可确定n为任一定值的过程在图中的相对位置。

对比p-υ，图和T-s图还可看出，要判断过程中的q及Δu、Δh的正负，用T-s图较为方便，因一切自左向右进行的过程，熵均增加，即d＞0。又因T总是正值，故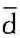q＝Tds＞0，必然是加热过程。相反，一切自右向左的过程，熵均减小，q为负值，必然是工质的放热过程。在T-s图上一切自下而上的过程，dT＞0，理想气体的Δu＞0，Δh＞0；相反，一切自上而下的过程， dT＜0，则Δu＜0，Δh＜0。判断膨胀功的正负，则用p-υ图较方便。以定容线为界，向右进行值。那么，如何在p-υ图上判断q及Δu、Δh的正负，在T-s图上判断功的止负呢？我们以T的过程，比体积增大，工质膨胀对外作功；向左进行的过程，比体积减小，工质被压缩，功为负s图上定容过程线为例来说明这个问题。

在T-s图上将某一定容线沿水平方向平移，可得一簇定容线υa，υb，υc，⋯。为比较不同定容线比体积的大小，任取两条定容线υb，υc，做一定温线与这两条定容线交于点b和点c，如图5-7所示。根据式（5-25a），从点b到点c比熵的变化量为

由上式可见，因为sc＞sb，所以υc＞υb。可见，定容线向右水平移动时比体积增大。因此，在T-s图上同样是以定容线为界，向右进行的过程，比体积增大，工质膨胀对外作功；向左进行的过程，比体积减小，工质被压缩，功为负值。可见，在p-υ图上判断q及Δu、Δh的正负，在T-s图上判断功的正负和我们上面所述的方法是相同的。

根据以上分析，明确了n在热力坐标图上的分布规律，即可确定某一过程在图中的相对位置，继而可判断该过程中膨胀功、热量、热力学能以及焓、熵的变化量的正负，从而不难定性地说明过程中的能量转换关系。例如，已知某一过程的n值为1＜n＜κ，则在p-υ图和T-s图上对应的曲线位置应在定熵线n＝κ与定温线n＝1之间。若又知该过程中工质的终态压力低于初态，则该过程曲线位置必然是自左向右进行。因此，由图不难看出该过程中能量转换关系应为w＞0，Δu＜0，q＞0。

图5-7 定容过程在T-s图上的移动

例5-5 气缸与活塞间封闭有1kg某种理想气体。该气体经历一多变压缩过程，消耗压缩功300kJ，气体的比体积缩小1/7.5，压力增大到9.3倍。已知该气体的κ＝1.4和cv＝0. 716kJ/（kg·K）。试按定比热容计算过程的多变指数、气体被压缩的终温、气体热力学能和熵的变化量，以及过程中气体与外界交换的热量。

解根据题意已知：w＝﹣300kJ/kg，υ2＝υ1/7.5，p2＝9.3p1。

（1）求多变指数

（2）求气体被压缩的终温

多变过程的比热容为

根据已知条件υ2＝υ1/7.5和p2＝9.3p1，可得

根据状态方程有

所以

T2＝1.24T1

热力学能的变化量为

Δu＝cv（T2－T1）＝0.716×（1.24T1－T1）＝0.172T1

根据热力学第一定律求多变过程的热量为

q＝Δu＋w ＝0.172T1－300

根据多变过程的定比热容求多变过程的热量为

q ＝cn（T2－Tt）

＝﹣1.961×（1.24T1－T1）＝﹣0.471T1

显然，以上两式应相等，有

0.172T1－300＝﹣0.471T1

所以

T2＝1.24T1＝1.24×466.56＝578.53K

（3）求气体热力学能和熵的变化量

（4）求气体的放热量

q＝Δu＋w ＝90.17－300＝﹣219.83kJ/kg

为便于分析比较，表5-3集中列出了理想气体可逆过程的计算公式。

表5-3 理想气体可逆过程计算公式表

复习思考题

1.水蒸气在什么情况下可看作是理想气体？

2.通用气体常数与气体常数有何不同？VM，n＝（22.414±0.003）和RM＝8314 J/（kmol·K）是否在任何条件下都适用？与气体的种类和所处状态是否有关？

3.理想气体的比定压热容和比定容热容都随温度变化，那么它们的差值是否也随温度变化？它们的比值呢？(www.xing528.com)

4.气体的比热容到底是定值还是变值？为什么有变比热容又有定比热容？变比热容为什么又有所谓曲线关系和直线关系之分？

5.与一般工质比较，理想气体的热力学能和焓有什么特点，如何计算理想气体的热力学能和焓的变化量？

6.热力学第一定律的数学表达式可写成

q＝Δu＋w

或

两者有何不同？

7.如图5-8所示，1—2和4—3各为定容过程，1—4和2—3各为定压过程，试判断q143与q123哪个大？

8.今有两个任意过程1—2和1—3，点2和点3在同一条绝热线上，如图5-9所示。试问Δu12与Δu13谁大谁小？又如点2和点3在同一条等温线上呢？

图5-8 复习思考题7用图

图5-9 复习思考题8用图

9.定温过程是等热力学能和等焓过程，这一结论对任意工质都成立吗？

10.气体在气缸内把从外界吸收的热量和本身热力学能的减少两者转换为对外界做膨胀功，试利用p-υ图或T-s图确定该过程的多变指数n的范围。

11.试讨论1＜n＜k的多变膨胀过程中气体温度的变化以及气体与外界热传递的方向，并用热力学第一定律加以解释。

12.在T-s图上将定容线和定压线分别向右移动，试问比体积和压力将怎样变化？

习 题

1.活塞式压缩机每分钟从大气中吸入压力为0.1MPa，温度为17℃的空气0.2m3。空气经压缩机压缩后充入空气瓶中，瓶的体积为5m3。瓶内充满空气时，表压力为3MPa，温度为50℃。在压缩机充气前，瓶内原来就有压缩空气，其表压力为0.5MPa，温度为17℃。试求要经过多少时间，压缩机才能把空气瓶充满。

2.在尺寸为5m×5m×6m的绝热密闭房间内有一个风扇，功率为200W。早上房间内温度为15℃。主人希望晚上返回时室内温度能有所降低，因此离开时打开风扇让其连续工作。试问当主人8h后返回时室温能否降低？变化多少？已知室内压力为0.101MPa。

3.有质量2kg初态为p1＝0.13MPa，t1＝27℃的氮气在定压下加热到127℃，求热力学能、焓和熵的变化量（按定比热容计算）。

4.柴油机气缸中的燃气在膨胀开始时p1＝8MPa，t1＝1800℃，膨胀终了时p2＝0.4 MPa，t2＝400℃，试求燃气（性质可视为空气）比熵的变化量，设膨胀过程为可逆过程，试按比熵的变化判断过程中燃气和外界热交换的方向。

5.绝热的刚性容器，其热容量可以忽略不计。若用一隔板将其分为A、B两个不相等的部分，其内各装有不同数量的同一种理想气体，如图5-10所示。气体状态参数初始值是已知的。试推导隔板抽出后气体的平衡温度和平衡压力表达式。假定气体的比热容为定值。

6.如图5-11所示，两股压力相同的空气流，一股的温度为t1＝400℃，流量qm1＝120kg/h；另一股的温度为t2＝150℃，流量qm2＝210kg/h；在与外界绝热的条件下，它们相互混合形成压力相同的空气流。已知比热容为定值，试计算混合气流的温度，并计算混合过程前后空气的熵的变化量是增加、减小或不变，为什么？

图5-10 习题5用图

图5-11 习题6用图

7.在柴油机气缸中，空气沿绝热线压缩。设初压p1＝0.14MPa，初温t1＝50℃，压缩终点温度t2＝650℃，试求压缩终点的压力和初、终比体积之比υ1/υ2。

8.如图5-12所示，气缸内装有空气，气缸的截面积A＝100cm2，活塞及其上负载的总质量为300kg。初始时气缸内空气温度为20℃，体积为0.001m3。整个设备放在室内，并处于平衡状态。如将活塞上的负载突然取去200kg，则气缸内的空气便迅速膨胀。假定整个膨胀过程是在绝热条件下进行的，且忽略活塞与气缸壁之间的摩擦，试求活塞上升的距离，以及绝热膨胀终了时气缸内空气的温度。

9.如图5-13所示，理想气体进行了一可逆循环1—2—3—1，已知3—1为定压过程，υ3＝2υt；2—3为定容过程，p2＝2p3；1—2为直线线段，即p/υ＝常数。

（a）试论证q1－2＞q1－3＋q3－2；

（b）画出该循环的T-s图，并证明Δs1－2＝Δs1－3＋Δs3－2

（c）若该理想气体的cp＝1.013kJ/（kg·K），c V＝0.724kJ/（kg·K），试求该循环的热效率。

10.图5-14所示的A与B是体积相等的两个刚性绝热容器，开始时它们都贮有温度T与压力p的同种理想气体。但容器A放出的气体可逆绝热地流经气轮机排向大气，而容器B放出的气体绝热地流经阀门排向大气。试问当A与B中的压力降为一半时，气轮机与阀门出口处的气体温度各为多少？

图5-12 习题8用图

图5-13 习题9用图

11.有1kmol理想气体从初态p1＝500kPa，T1＝340K绝热膨胀到原来体积的2倍。设气体c M，p＝33.44kJ/（kmol·K），c M，V＝25.12kJ/（kmol·K）。试确定在下述情况下气体的终温、对外所做的功及熵的变化量。

（1）可逆绝热过程；

（2）气体向真空进行自由膨胀。

图5-14 习题10用图

图5-15 习题12用图

12.在一个绝热的封闭气缸中配有一无摩擦的导热活塞，活塞将气缸分为左、右两部分，如图5-15所示。初始时活塞被固定在气缸中间，左、右两部分体积相等。左半部分中盛有温度为300K、压力为0.2MPa的0.001m3空气，右半部分盛有温度为300K、压力为0.1MPa的0.001m3空气。求活塞释放后，空气达到新的温度和压力平衡时其温度、压力及熵的变化量。

13.如图5-16所示，VA＝VB，A中装有空气t A＝25℃，p A＝2MPa，B为绝对真空，求A与B两容器连通后，空气的压力、温度、热力学能、焓及单位质量工质熵的变化。假定整个容器和外界是绝热的。

图5-16 习题13用图