理想气体的热力过程优化

一、研究热力过程的目的和方法

热能和机械能的相互转换，通常总是通过气态工质在热力设备中进行吸热、膨胀、放热、压缩等一些热力状态变化过程而实现的。工质热力过程的分析和计算的目的在于揭示过程中工质状态参数的变化规律，以及该过程中热能与机械能之间的转换情况，进而找出影响它们转换的主要因素。

热力设备中的实际过程是很复杂的。首先，严格说来，都是不可逆过程，其次，工质的各状态参数都在变化，不易找出规律，故实际过程不易分析。但仔细观察热力设备中常见的一些过程，发现它们却又往往近似地具有某一简单的特征。例如，汽油机工作时，气缸里被压缩了的汽油蒸气和空气的可燃混合气体被电火花点燃，在一瞬间迅速燃烧，活塞来不及移动，气体的压力和温度迅速升高，这个过程可以被看做是定容过程等等。此外还有定压、定温和绝热等基本热力过程。但是，工程上的能量传递与转换过程不限于上述四种基本热力过程，在许多热力过程中往往是工质的所有状态参数都发生变化，而且与外界有功和热量的交换，此时不能再用这四种中任一基本热力过程方程来描述它。因而，必须找到一个普遍的、且按某种规律变化的过程方程。这就是我们在这一章中要讨论的多变过程。

本章主要讨论理想气体的可逆热力过程，对于不能作为理想气体看待的工质如水蒸气、氨等，其热力过程的分析计算应借助于图表进行。分析计算理想气体的热力过程，其方法归纳起来有如下几点：

1.根据过程特点，利用状态方程及热力学第一定律解析式，求出过程方程p＝f（υ）。

2.借助过程方程并结合状态方程找出不同状态时参数间的关系式，从而根据已知的初态参数求得终态参数，或者反之。

3.在p-υ图和T-s图上表示出该过程曲线。

4.确定过程中工质的功、热量以及热力学能、焓、熵的变化。

因为理想气体的比热力学能和比焓仅是温度的函数，所以理想气体任何过程的比热力学能和比焓的变化量都可按下式计算：

Δu＝c V（t2－t1） Δh＝cp（t2－t1）

比熵也是状态参数，在初、终状态参数确定后，可按式（5-25）计算该过程的比熵变化量。

功和热量是过程量，其数值随热力过程和工质性质而异。闭口系统可逆过程对外输出膨胀功

开口系统可逆过程对外输出技术功

过程热量在求得功和热力学能以及焓的变化量之后，可按热力学第一定律求得c

二、多变过程及其分析

1.过程方程

多变过程的定义式为

pυn＝常数 （5-26）

式中，指数n可以是任何实数。n值不同，状态变化的规律也不同，即不同的热力过程具有不同的n值。因此，式（5-26）可用来描述无限多个热力过程的变化规律。凡状态变化规律符合式（5-26）的热力过程都称为多变过程。每一个确定的多变过程都具有一个不变的指数n，n叫做多变指数。四个基本过程都是多变过程在n取不同数值时的特例：

当n＝0时，pυ0＝p＝常数，定压过程；

当n＝1时，pυ＝常数，定温过程；

当n＝k时，pυκ＝常数，绝热过程。式中κ为比定压热容与比定容热容之比，即κ＝cp/c V，称为绝热指数，其数值随气体的种类和温度而变。因为cp＞c V，所以κ＞1。如近似地取比热容为定值，则κ也是定值。对于空气和燃气，κ＝1.4。

当n＝±∞时，因为pυn＝常数开n次方，得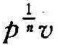＝常数，所似＝p0υ＝常数，即定容过程。

2.初、终参数关系(www.xing528.com)

根据多变过程方程pυn＝常数和理想气体状态方程pυ＝RT，可以导得多变过程初、终状态的参数关系式为

3.热力学能、焓和熵的变化量

多变过程的比热力学能和比焓变化量为

Δu＝cv（T2－T1） （5-30）

Δh＝cp（T2－T1） （5-31）

根据式（5-25）和式（5-28）可求得多变过程比熵的变化量为

4.功和热量

在多变过程中，由于pυn＝常数，故闭口系统体积功为

即

或

以上三式是完全等效的，可根据给定的已知条件，任选其中一式计算多变过程的体积功。

对稳定流动开口系统，多变过程的技术功为

可见，多变过程的技术功是体积功的n倍。

多变过程的热量可按热力学第一定律确定，即

根据迈耶方程及比热容比，可得

令

式中，cn为理想气体多变过程的比热容。

分析式（5-36）可知：

当n＝0时，c0＝κcv＝cp，定压过程的比热容；

当n＝1时，c1＝c ，为定温过程的比热容，这是因为在定温过程中，外界无论加给气体多少热量，气体的温度均不发生变化；

当n＝κ时，cκ＝0，为绝热过程的比热容；

当n＝±∞时，c±∞＝c V，为定容过程的比热容。

从式（5-36）还可以看出，因为cv＞0，当1＜n＜κ时，cn为负值。这说明气体吸热而温度下降，这是因为气体对外界作的功大于气体吸收的热，因而气体的热力学能减少；或者气体放热而温度升高，这是因为外界对气体作的功大于气体放的热，因而气体的热力学能增加。