理想气体比热容的探究

一、比热容及其分类

单位质量的物体在准静态过程中温度升高1K所需的热量称为“比热容”。其定义式为

按照计量的单位，比热容可分为三类，取1kg质量作为计量单位时，其比热容称为质量比热容，用符号c表示，单位为kJ/（kg·K）；取标准状态下1m3气体的体积作为计量单位时，其比热容称为体积比热容，用符号c表示，单位为kJ/（m3·K）；取1kmol作为计量单位时，其比热容称为千摩尔比热容，用符号CM表示，单位为kJ/（kmol·K）。三者之间的换算关系为

一般以质量比热容应用较普遍，下面以质量热容为主进行讨论。

因为热量与过程有关，所以比热容的数值也随过程的不同而异。在热工计算中，通常给出两种特定过程的比热容：即压力保持不变的定压过程的比热容，和比体积保持不变的定容过程的比热容，它们分别称为比定压热容和比定容热容。于是，由式（5-7），有

式（5-9）、（5-10）中，Cp和CV分别表示定压真实质量比热容和定容真实质量比热容。根据热力学第一定律的表达式，对于定压过程（dp＝0）和定容过程（dυ＝0），分别有

于是

对于理想气体，比热力学能仅为温度的函数，即

u＝u（T）

因此，由式（5-12）可得

根据比焓的定义式和理想气体的状态方程，可得

h＝u＋pυ＝u＋RT＝h（T）

可见，理想气体的比焓也仅为温度的函数，将上式代入式（5-11）可得

比定压热容较比定容热容大，因为气体在定压下受热要膨胀，即要克服外力作功，所以比定压热容大于比定容热容的量值就等于单位质量气体在定压下温度升高1K时对外所作的功。

二、应用比热容计算热量的方法

1.曲线关系

实验测定理想气体的比热容仅是温度的函数，且其函数关系甚为复杂，但总可表达为

c＝a＋bt＋et2＋⋯ （5-15）

在比热容-温度坐标图5-2上，式（5-15）可用曲线1—2表示。理想气体由t1℃升高到t2℃所需的单位质量热量按式（5-7）积分求得

图5-2 比热容与温度的曲线关系

式中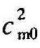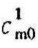，、分别代表温度自0℃到t1和0℃到t2的平均比热容。这种平均比热容，它们的起始温度相同，都是0℃。这样就简化了数据表的编制。表5-1中给出了0℃到t℃间的平均比热容值。然后利用式（5-16）可计算t1℃升高到t2℃过程的加热量。

2.直线关系

在工程上当没有比热容表时，常用平均比热容的直线关系计算热量，当温度变化范围不大时，由此得出的数值一般可以满足工程上的要求。取式（5-15）右侧的前两项，即可得真实比热容的直线关系式(https://www.xing528.com)

c＝a＋bt （5-17）

这时，近似地将比热容看做与温度成直线关系，如图5-3所示，即以一条近似的直线代替实际上的曲线。此时热量

于是，可得到t1℃到t2℃间的平均比热容

该平均比热容可利用表5-2所列出的气体平均比定压热容和比定容热容直线关系式求得。表中所列出关系式中的t用（t1＋t2）代入即可求出t1℃到t2℃之间的平均比热容。

3.定值比热容

图5-3 比热容与温度的直线关系

尽管实际上气体的比热容是随温度的升高而增大，它是温度的复杂函数。但是，当气体温度较低且变化范围不大时，或者在精确度要求不高时，工程上为了简化计算，比热容可近似地当做定值，通常称为定值比热容。这时

q ＝c（t2－t1） （5-19）

定值比热容可采用下列数值：

单原子气体 c M，p＝20.9kJ/（kmol·K）

双原子气体 c M，p＝29.3kJ/（kmol·K）

三原子气体 c M，p＝37.7kJ/（kmol·K）

例5-3 试分别利用比热容表5-1和比热容表5-2，计算100kg二氧化碳在定压下从900℃加热到1300℃所需的热量，并进行比较。

解 查表5-1

按直线关系计算，查表5-2得

将t＝900＋1300＝2200℃代入上式，得从900℃到1300℃的平均比热容为

与按比热容表5-1算得的数据相比，两者之差为

56072－52220＝3852kJ

相对误差为

可见，温度在900～1300℃这样的范围内，对于双原子气体，如上例的空气，按直线关系式计算误差很小。而对于二氧化碳等三原子气体，按直线关系式计算误差较大，最好按比热容表5-1计算。

表5-1 气体的平均比定压热容（曲线关系）

表5-2 气体的平均比定压热容和平均比定容热容（直线关系）（适用范围：0～1500℃）