熵增原理：水和铁达到最大熵的平衡温度及熵变量

将式（4-14）

应用于孤立系统，因Q＝0，可得

式中，dSiso为孤立系统熵的变化量。式（4-19）说明，在孤立系统中，如进行的过程是可逆过程，其熵保持不变；如为不可逆过程，其熵增加；不论进行什么过程，其熵不可能减少。这就是孤立系统熵增原理，或简称熵增原理。熵增原理也是热力学第二定律的一种表述。因此，热力学第二定律也可称为熵定律，式（4-19）可作为热力学第二定律的数学表述。

值得指出，不论进行什么过程，孤立系统中的个别物体（子系统）的熵可以增加，也可以减少或不变，但孤立系统总体熵是永远不会减少的。

由孤立系统熵增原理可得出下列重要推论：

1.因为孤立系统的熵增加量是由过程的不可逆因素产生出来的，所以熵增加量（即熵产）可作为过程不可逆性的度量。

2.根据孤立系统的熵变化可判断过程进行的方向：如ΔSiso＞0，为不可逆过程，这是实际可以进行的过程；ΔSiso＝0，为可逆过程，这是理想极限情况；ΔSiso＜0，这是不可能实现的过程。

3.由熵增原理，可得孤立系统的平衡条件为

这是因为由有限物体组成的孤立系统内不可逆过程得以进行，是其内部的压力差、温度差等不平衡“势”的驱使。随着不可逆过程的进行，孤立系统的熵不断增加，而这种势差却不断减少。达到平衡时，势差消失了，熵增的原因也消失，孤立系统的熵便达到最大值。

例4-4 如图4-10所示，量热器中有2kg、20℃的水和0.5kg、500℃的铁块，它们的比热容分别为＝4.186kJ/（kg·K）和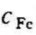＝0.4605kJ/（kg·K）。试按熵增原理论证当量热器中的水和铁的总熵达到最大值时，水温和铁块的温度相等，并求出此平衡温度（略去量热器的热容量和向环境的散热）及这一过程中水和铁块的总熵变化量。

图4-10 例4-4用图

解 按题意，取量热器内的水和铁块为孤立系统。设不可逆热交换过程中水和铁块的瞬时温度分别为和。

按热力学第一定律

式中

所以

按熵增原理，系统达到平衡时，Siso→max，即

对水和铁块的热交换分别设想两个可逆过程，则水和铁块微元熵变分别为

将式（c）和（d）代入（b），可得

将式（a）代入式（e），可得

可见孤立系统总熵达到极大值时，水和铁块温度相等，即系统处于热平衡，此时系统的温度为平衡温度T。

对式（a）进行积分

于是可得

式中，和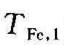分别为水和铁块的初温。此式即为常用的热平衡方程。可见，这一简单的热平衡方程也是热力学第一定律和第二定律的综合结果，而决不是仅仅由热力学第一定律就能建立的。由上式，可得平衡温度为

或

对式（c）和式（d）进行积分，可求得这一过程中水和铁块的熵变化量为

孤立系统（水和铁块）总熵的变化量为

复习思考题

1.热力学第二定律可否表述为：功可以完全变为热，但热不能完全变为功，为什么？

2.“循环功越大，则热效率越高”；“可逆循环热效率都相等”；“不可逆循环效率一定小于可逆循环效率”；“自发过程是不可逆过程，则非自发过程就是可逆过程”。这些结论是否正确？为什么？

3.自然界中一切过程都是不可逆过程，那么研究可逆过程又有什么意义呢？

4.下列说法是否正确，为什么？

（1）熵增大的过程为不可逆过程；

（2）不可逆过程ΔS无法计算；

（3）若从某一初态经可逆与不可逆两条途径到达同一终态，则不可逆途径的ΔS必大于可逆途径的ΔS；

（4）工质经不可逆循环，ΔS＞0；

（5）工质经不可逆循环，由于，所以；

（6）可逆绝热过程为定熵过程，定熵过程就是可逆绝热过程；

（7）自然界的过程都朝着熵增大的方向进行，因此熵减过程不可能实现；

（8）加热过程，熵一定增大；放热过程，熵一定减小。

5.某封闭系统经历了一不可逆过程，系统从外界吸热为20kJ，同时对外界作膨胀功为10 kJ。(www.xing528.com)

（1）按热力学第一定律计算系统热力学能的变化量；

（2）按热力学第二定律判断系统熵的变化（为正、为负）。

6.某封闭系统经历了一不可逆过程，系统向外界放热为10kJ，同时外界对系统作功为20 kJ。

（1）按热力学第一定律计算系统热力学能的变化量；

（2）按热力学第二定律判断系统熵的变化（为正、为负、可正可负亦可为零）。

7.p-υ图和T-s图的重要性各何在？不可逆过程在这两个图上怎样表示？

8.某封闭系统经历了由几个简单的可逆过程（如定温、绝热、定压和定容）连结而成的复杂变化过程，如只知道这一复杂过程终态的熵大于初态的熵，就能确定该过程中系统从外界吸热吗？同样，如只知道这一复杂过程终态的比体积大于初态的比体积，就能确定该过程中系统对外界作膨胀功吗（提示：分别运用T-s图和p-υ图说明）？

习题

1.设工质在某热机循环中从高温热源吸热500kJ，向低温热源放热300kJ，试求循环热效率和工质对外作的净功。

2.设工质在某制冷循环中向高温热源放热1000kJ，消耗外界的机械功为200kJ，试求工质从低温热源吸收的热量和制冷系数。

3.设一可逆卡诺热机中工作于1600℃和300℃的两个热源之间，工质从高温热源吸热400kJ，试求：（1）循环热效率；（2）工质对外作的净功；（3）工质向低温热源放出的热量。

4.设一可逆卡诺热机中工质向温度为500℃的低温热源放出的热量为200kJ，热效率为50％，试求：（1）工质从高温热源吸收的热量以及高温热源的温度；（2）工质对外作的净功。

5.设一逆向可逆卡诺循环中工质从﹣10℃的低温热源吸收的热量为800kJ，制冷系数为8.5，试求：（1）工质向高温热源放出的热量以及高温热源的温度；（2）外界对工质作的净功。

6.有一半导体制冷装置，需用端电压E＝24V、电流Ⅰ＝30A的电功率，每小时可从这一装置的小冰箱中吸热2680kJ，求该装置的制冷系数ε和它的热接点向大气每小时的散热量？

7.热泵循环中传给高温热源的热量q1与所消耗的净功w（q1与w均取绝对值）之比称为供热系数εh，即

试推导卡诺热泵循环的εc.h公式。

8.试论证如违反热力学第二定律的克劳修斯说法，则必然违反开尔文说法。

9.试用热力学第二定律证明，p-υ图上任意两条可逆绝热线不能相交。

10.有A，B两物体，其初温TA＞TB，两物体的质量相等m A＝m B＝m，其比热容亦相等CA＝CB＝C，且为常数。可逆热机在其间工作，从A吸热，向B放热，直至两物体温度相等时为止。

（1）试证明平衡时的温度为

（2）求出可逆热机对外输出的净功。

11.有A，B两可逆热机，它们的循环分别如图4-11（a）和（b）所示。

（1）试证明ηA/B＝1＋TL/TH；

（2）如TH＝800K，TL＝300K时，求出两可逆热机的热效率各为多少。

12.某热机循环中，工质先从T′H＝600K的第一热源吸收热量Q′1，再从T″H＝800K的第二热源吸收热量Q″1，向TL＝300K的冷源放出热量Q1，循环净功为W。在下列条件下，试分别判断该热机循环是可逆的、不可逆的或不可能实现的：

（1）Q′1＝1200J，Q″1＝400J，W＝800J；

（2）Q′1＝1200J，Q″1＝400J，Q2＝750J；

（3）Q″1＝400J，Q2＝750J，W＝900J。

13.如图4-12所示，用热机E带动热泵P工作，热机在热源T1和冷源T0之间工作，而热泵则在冷源T0和另一热源T′1之间工作。已知T1＝1000K、T′1＝310K、T0＝250K。如热机从热源T1吸收热量Q1＝1kJ，而热泵向另一热源T′1放出的热量QH供冬天室内取暖用。

（1）如热机的热效率为ηt＝0.50，热泵的供热系数εh＝4，求QH；

（2）如热机和热泵均按可逆循环工作，求QH

（3）如上述两次计算结果均为QH＞Q1，表示冷源T0中有一部分热量传入了温度T′1的热源，而又不消耗（除热机E所提供的功之外的）其他机械功，这是否违反热力学第二定律的克劳修斯说法？

14.按习题4-10给定条件，如将A，B两物体在与外界绝热的条件下直接接触而进行热传递，直至两物体温度相等时为止。

（1）试证明此时的平衡温度

（2）试求这一不可逆热传递过程的熵产及作功能力的损失（环境温度为T0）。

图4-11 习题11用图

图4-12 习题13用图

15.为了帮助理解式（4-19）是热力学第二定律数学表达式，试用孤立系统熵增原理论证：（1）热力学第二定律的克劳修斯说法；（2）热力学第二定律的开尔文说法；（3）卡诺定理。

16.试用孤立系统熵增原理，对习题13的第三个问题作出确切的分析。