系统状态参数：熵的重要性

历史上，熵是克劳修斯根据热力学第二定律在引用热力学温度对卡诺定理作了数学表述的基础上提出的。

克劳修斯积分式（4-6）是将卡诺定理推广应用于任意可逆循环而导出的结果。现进一步把卡诺定理推广应用于任意可逆过程。如图4-6所示，在p-υ图上有一任意可逆过程1a2。为研究沿该可逆过程的克劳修斯积分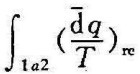具有什么性质，从终态2作任意一个可逆过程2b1，与原可逆过程1a2组成一个可逆循环1a2b1。对这一可逆循环，应用式（4-6）可得

图4-6 熵的引出用图

于是

因2b1为可逆过程，可以沿原过程经历的每一步逆向进行，只是系统与外界交换的热和功符号相反，所以

因初态1和终态2之间可作无数条可逆线，于是

可见，只要初态1和终态2一定，沿1到2之间的任意可逆过程的克劳修斯积分均有相等的数值。换言之，沿可逆过程的克劳修斯积分只与系统的初、终状态有关，而与可逆过程的途径无关。因而，它表示了系统某一状态参数的变化量。这个状态参数称之为熵，单位质量工质的熵称为比熵，分别以符号S和s表示，其单位分别为kJ/K和kJ/（kg·K）。于是

对于微元可逆过程，有

因为式（4-6）与工质性质无关，所以式（4-9）和式（4-10）也与工质性质无关，即任何工质都存在状态参数——熵。式（4-10）就是熵的定义式。

由上述讨论可见，熵的引出是把两给定热源间所有卡诺循环热效率均相等而与工质性质无关这一客观规律，推广应用于可逆过程的必然结果。因此，任何工质都有状态参数——熵，就像任意工质都有压力、温度和体积一样，是客观存在的事实，而不是人们凭空捏造出来的。只不过熵不能用仪表直接测示，因而人们通过比较抽象的数学推导才把它的存在揭示出来。

二、沿不可逆过程的克劳修斯积分

如图4-7所示，p-υ图上有一不可逆过程1a2，沿该过程的克劳修斯积分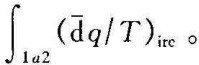前已指出，熵是系统的状态参数，只要系统的初、终状态一定，熵的变化量就有确定数值，而与过程是否可逆无关。为了求得不可逆过程1a2熵的变化量，可在初、终状态之间任意作一假想的可逆过程1b2（见图4-7），沿可逆过程1b2的克劳修斯积分就是不可逆过程1a2熵的变化量。按式（49），比熵的变化量为

图4-7 沿不可逆过程的克劳修斯积分

下面讨论沿不可逆过程的克劳修斯积分与其熵的变化量之间的关系。如图4-7所示，p υ图上1a2b1组成一个不可逆循环，其中1a2为不可逆过程，2b1为可逆过程。按式（4-7），对不可逆循环1a2b1有

因为2b1为可逆过程，所以有

综合以上两式，可得

对于微元不可逆过程，有

由式（4-11）可见，沿不可逆过程的克劳修斯积分恒小于该过程中熵的变化量。这个结论，实质上是两热源间不可逆循环的热效率恒小于相同热源条件下卡诺循环热效率这一客观规律推广应用于不可逆过程的结果。

将式（4-9）和式（4-11）合并，可得

对微元过程，有

式（4-13）、（4-14）中，等号适用于可逆过程，不等号适用于不可逆过程。无论什么过程，系统熵的变化量决不可能小于沿该过程的克劳修斯积分。这是由热力学第二定律所揭示的一切过程的共性。因此，只要所研究的系统是由大量分子（或其他微粒）所组成，则该系统进行的过程，除了遵守能量守恒（热力学第一定律）之外，还必须同时遵守熵变化量不小于沿该过程的克劳修斯积分这一规律（热力学第二定律）。只有同时遵守这两条规律的过程才是可能实现的。这样，对过程方向性的研究，从理论上深化为对系统本身的状态参数熵的研究。

三、熵流与熵产

为了准确地表述熵与过程方向性的关系，下面介绍熵流与熵产的概念。沿任何过程（可逆或不可逆）的克劳修斯积分，称为“熵流”，以符号ΔSf表示，即

将过程中系统熵的变化量（S2－S1）与熵流ΔSf之差定义为“熵产”，以符号ΔSg表示，即

于是

可见，过程中系统熵的变化量是由熵流和熵产两部分组成的。其中，熵流是由于系统与外界发生热交换而引起的，式（a）中的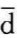Q为热源与系统交换的微元热量，T为相应热源的温度。由式（a）可以看出，当系统从热源吸热时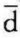，Q＞0，ΔSf＞0；反之，当系统向热源放热时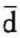，Q＜0， ΔSf＜0。因此，熵流可以是正值，也可以是负值，它是系统与热源之间通过热交换而发生的熵的交换。而熵产，则由式（4-13），可得(www.xing528.com)

式中，等号适用于可逆过程，不等号适用于不可逆过程。可见，在可逆过程中，熵产为零，熵的变化量等于熵流，换言之，系统只与热源发生熵的交换（系统得到的熵在数值上等于热源失去的熵，或系统失去的熵在数值上等于热源得到的熵）。在不可逆过程中，熵产大于零，熵的变化量大于熵流，换言之，系统除了与热源发生熵的交换之外，在不可逆过程中还有熵产生了。不可逆过程中系统熵产生的原因在于过程中所包含的不可逆因素（耗散效应、有限温差的热传递、自由膨胀和不同工质的混合等）使机械功、动能等可用能转变为热量。不可逆因素的影响越小，熵产也越小；当这种影响趋近于零时，熵产也就趋近于零。因此，熵产是衡量过程不可逆性的尺度。

总之，熵流是热量交换的结果，熵产是热量产生的结果。系统熵的变化量等于熵流与熵产之和，它可以大于零、等于零或小于零，但任何过程中熵产不可能小于零。

四、熵的性质

1.熵是系统的状态参数，为尺度量，具有可加性。如系统由几个子系统组成，则系统熵的变化量ΔS为各子系统熵的变化量ΔS1，ΔS2，ΔS3，⋯的代数和，即

ΔS＝ΔS1＋ΔS2＋ΔS3＋⋯

对于均匀系统，则为

2.熵的定义式为据此，可仿照p-υ图，建立以热力学温度为纵坐标、比熵为横坐标的温熵图（T-s图）。如图4-8所示，系统的初态（T1，s1）用点1表示，终态（T2， s2）用点2表示，从初态到终态的某一可逆过程可用曲线1-2表示。

因为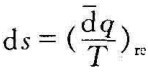，所以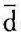q＝Tds。在微元可逆过程中，单位质量的工质从热源吸收的热量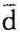q在Ts图上可用画阴影线的微元面积表示。因此，在可逆过程1—2中，单位质量工质从热源吸收的热量为

图4-8 系统的温熵图

可见，4-8图上过程曲线下的面积表示可逆过程中单位质量工质所吸收的热量。

对于实际过程中系统与热源之间热交换的方向，可以从系统与热源之间的温差来断定。但对于可逆过程，系统与热源的温差无限小，因此无法用两者的温差来判别，这时可用系统比熵的变化来判别。由式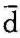q＝Tds可以看出，因热力学温度T总是大于零，在可逆过程中，如ds＞0，则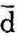q＞0，即比熵增加时，系统从热源吸热；反之，如ds＜0，则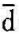q＜0，即比熵减少时，系统向热源放热；当ds＝0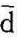，q＝0，即比熵不变，系统与热源无热交换。因此，可逆的绝热过程为定熵过程。

3.熵产是过程不可逆性的度量。熵产等于零，为可逆过程，这是实际过程的理想极限情况；熵产大于零，为不可逆过程，而且熵产越大，过程的不可逆性也越大；熵产小于零的过程是不可能实现的。

对于不可逆绝热过程，其熵流等于零，而熵产大于零，其熵的变化量大于零。因此，不可逆绝热过程为熵增加的过程。

例4-2 在压力为0.1013MPa时，用500K的恒温器把1kg、100℃的水加热成为100℃的水蒸气，需要热量2257kJ/kg，试求这一过程中工质（水和水蒸气）比熵流、比熵的变化量和比熵产的数值。

解取汽化中的水和水蒸气为封闭系统，其初态1为0.1013MPa时100℃的水，终态2为0.1013MPa时100℃的水蒸气。系统的初、终状态是确定的，且均为平衡态。外界为500 K的恒温器（热源）。因此，系统的比熵流为

因为在系统的吸热过程中，热源与系统之间的温度差为500－373.15＝126.85K，所以这一吸热过程为不可逆过程。因此，比熵的变化量大于比熵流。为了计算这一不可逆过程比熵变化量的数值，如图4-9所示，设想500K的热源把热量先传给温度Tm＝373.15K的中间热源，然后这一中间热源再把热量在温差为无限小的条件下传给系统，使系统从初态1变化到终态2。显然，系统从中间热源的吸热过程为可逆过程。因此，系统的比熵变化量等于这一设想的可逆过程的比熵流，即

比熵产为

可见，比熵产大于零。由上式还可以看出，这一不可逆过程中比熵产大于零的原因是热源的温度T大于系统的温度Tm，即T＞Tm，而且两者的温差（T－Tm）越大，比熵产就越大。同时还可以看出，如比熵产小于零，则要求T＜Tm，即要求用比系统温度低的热源将热量自发地传给系统，显然这是违反热力学第二定律的，因而是不可能实现的。

图4-9 例4-2用图

例4-3 在压力为0.1013MPa时，用外界的功源通过搅拌器的摩擦把1kg、100℃的水加热成为100℃的水蒸气，需要功量2257kJ/kg，试求这一过程中工质（水和水蒸气）比熵流、比熵的变化量和比熵产的数值。

解 本例的解法与上例类似。取汽化中的水和水蒸气为封闭系统。外界只有功源，而没有热源。因此，系统与外界没有热交换，比熵流为

因为在系统的吸热过程中，系统吸收的热量，是由在其中的搅拌器将功源提供的功量通过摩擦转换而来的，所以这一吸热过程为不可逆过程。因此，比熵的变化量大于比熵流。为了计算这一不可逆过程中比熵变化量的数值，设想功源提供的功量通过摩擦变为热量的过程在373.15K的中间热源中进行，然后这一中间热源再把热量在温差为无限小的条件下传给系统。与上例相同的理由，系统的比熵变化量为

比熵产为

本例中比熵产大于零的原因是由于存在耗散效应，即功通过摩擦变热。由上式还可以看出，摩擦变成的热量q1→2越大，吸收此热量的系统温度Tm越低，则比熵产就越大。