克劳修斯积分式的原理与应用

热力学第二定律的基本任务是研究能量转换过程的方向性。以上仅讨论了特定情况下的转换规律，即热量在两热源之间，通过循环转换为功的能力——循环热效率。现在我们要把这个结果加以推广和扩充，使之更具有普遍的意义。为此，克劳修斯曾引用热力学温度对卡诺定理作了数学的表述，得出克劳修斯积分式，从而把着眼点从热量转换为功的能力，转移到工质热力状态变化规律上来，找到了状态参数——熵，使热力学第二定律关于能量转换规律的论述更为普遍和深入。这一节介绍克劳修斯不等式。

一、两热源间的循环

由卡诺定理和卡诺循环，可得

式中，T1和T2分别为高温热源和低温热源的热力学温度，在可逆循环中它们也分别是工质吸热和放热时的温度；q1和q2分别为高温热源加给工质的热量和低温热源吸收工质的热量，在可逆循环中它们也分别是工质吸收和放出的热量；等号适用于可逆循环，不等号适用于不可逆循环。由式（4-4）可得

如把上式中q2取代数值，则得

式（4-5）实质上是引用了热力学温度的卡诺定理的数学表述。它说明在两热源之间的循环中，工质从热源吸收的热量（放热为负）被相应热源的绝对温度所除而得的商的代数和，在可逆时为零；在不可逆时小于零；而绝对不可能大于零。这个结论具有原则性的意义，因为如果大于零，则违反了热力学第二定律。

二、无穷多个热源间的任意循环

下面将式（4-5）推广应用于无穷多个热源间的任意循环。如图4-4所示，在p-υ图上画有一任意可逆循环abcda。用无穷多条相互无限接近的可逆绝热线来分割这一循环，于是可得无穷多个微元可逆循环。取其中任一微元可逆循环efhge，因绝热线fh和eg无限接近，e和f两点无限接近，ef线可认为是微元可逆定温吸热过程线，同理，hg线可认为是微元可逆定温放热过程线，所以efhge可认为是两热源间的微元卡诺循环。由于这一系列的微元卡诺循环的吸热线和放热线分别与原循环相应的线重合，所以无穷多个微元卡诺循环吸热量之和与放热量之和分别与原循环的吸、放热量相等。此外，分割用的可逆绝热线均为相邻微元卡诺循环所公用，如fh线在前一循环中为压缩线，而在后一循环中为膨胀线，膨胀功与压缩功互相抵消。微元卡诺循环所作净功的总和与原循环的净功相等。因此，微元卡诺循环的总和与原循环在热和功方面都等效。从这里也可以看出，任意可逆循环要求有温度连续变化的无穷多个热源。

图4-4 任意可逆循环

根据式（4-5），对任一微元卡诺循环有

于是，对于无穷多个微元卡诺循环的总和有

即对任意可逆循环动abcda有

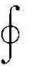表示沿封闭曲线abcda积分。

式（4-6）称为克劳修斯积分式，它说明在无穷多个热源间的任意可逆循环中，克劳修斯积分等于零。

如图4-5所示，不可逆循环abcda由不可逆过程abc（在p-υ图上用虚线表示）和可逆过程c减a组成。按上述用可逆绝热线分割的方法，同样可将原循环分成无穷多个微元循环的总和。所不同的是无穷多个微元循环中有部分或全部为相应的两热源间的不可逆循环。(www.xing528.com)

图4-5 任意不可逆循环

根据式（4-5），对其中的微元卡诺循环有

对其中的微元不可逆循环有

对任意不可逆循环总的有

式（4-7）称为克劳修斯积分不等式，它说明在无穷多个热源间的任意不可逆循环中，克劳修斯积分小于零。

综合式（4-6）和式（4-7），可得

式中，等号适用于可逆循环，不等号适用于不可逆循环。式（4-8）是卡诺定理推广应用于多热源或无穷多热源之间的任意循环而得出的数学表达式，它说明沿任意循环的克劳修斯积分绝对不可能大于零。这是一切循环的共性，是由热力学第二定律所确定的。换言之，如果大于零，则必然违反克劳修斯说法或开尔文说法。

例4-1 某热机中工质先从T′1＝1000K的热源吸热150kJ/kg，再从T″1＝1500K的热源吸热450kJ/kg，向T2＝500K的热源放热360kJ/kg，试判断该循环能否实现；是否为可逆循环？若令该热机做逆循环，即作制冷机用，工质能否从T2＝500K的热源吸热360kJ/kg，并向T″1＝1500K的热源放热450kJ/kg，以及向T′1＝1000K的热源放热150kJ/kg？

解 因热源超过两个，无法直接用卡诺定理判断。此题只能用式（4-10）判断。

1.作热机时为正循环，所以

此正循环是可以实现的，且为不可逆循环。

2.作制冷机时为逆循环，所以

因为克劳修斯积分大于零，这是违反热力学第二定律的，因而是不可能实现的。

上述计算表明，按此工作参数做正循环时，此热机为不可逆热机，必然在外界遗留了一个不可逆的变化量，如热从高温处自发地传到低温处或功通过摩擦变热，这些外界变化是不可能用任何方法消除掉的。如果此逆循环能实现，则必然导致热可以自发地从低温处传到高温处或热可以通过摩擦变功这类结论，而这是违反热力学第二定律的。