封闭系统热力学第一定律表达式探究

如图3-3所示，取气缸中质量为mkg的工质为封闭系统，其外界为热源和功源。当热源给系统加热量Q、系统对功源作膨胀功W时，按能量转换与守恒定律，输入系统的能量为Q，系统输出的能量为W，系统热力学能的变化量为ΔU＝（U2－U1），它们三者之间的关系由式（3-1）得

Q－W＝ΔU或Q＝ΔU＋W（3-10）

式（3-10）为封闭系统热力学第一定律的数学表达式。

图3-3 封闭系统与外界的能量转换

对于单位质量的封闭系统，式（3-10）可写为

对于一个微元过程，可写为

以上三式为封闭系统热力学第一定律的三种表达式。它们说明热源加给封闭系统的热量用于系统热力学能的增加和对功源作的膨胀功。上述公式中的q、Δu和w都是代数值，即

q＞0，表示热源对系统加热；q＜0，表示系统向热源放热。

Δu＞0，表示系统比热力学能增加；Δu＜0，表示系统比热力学能减少。

w＞0，表示系统对功源作功；w＜0表示功源对系统作功。(www.xing528.com)

从上述三式可以看出，当初、终态给定时，热力学能的变化量为定值，但过程不同时，膨胀功有不同数值，因而热量也有不同数值。这就具体地说明热量不是状态参数，而是过程函数。上述三式是由普遍适用的能量转换和守恒定律直接应用于封闭系统而导出的，所以，它们对任何工质和任何过程（可逆或不可逆过程）都是适用的。

对可逆过程，因为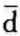w＝pdυ，所以封闭系统可逆过程的热力学第一定律为

例3-1 有一定质量的工质从状态1沿1A2到达终态2，又沿2B1回到初态1，并且Q1A2＝50kJ，U2－U1＝10kJ，W2B1＝﹣5kJ。试判断沿过程1A2工质是膨胀还是压缩，并且求工质沿1A2B1回到初态时的净吸热量和对外作的净功。

解 取工质为封闭系统，由式（3-10）得

W 1A2＝Q1A2－（U 2－U 1）＝50－10 ＝40kJ

因W 1A2＞0，系统对外界作膨胀功，所以工质膨胀。

系统从初态出发经过一系列的状态变化又回到初态，这样的闭合过程在热力学中称为循环。将式（3-10）应用于循环时，因为热力学能是系统的状态参数，系统经过循环又回到初态，热力学能的变化量为零。所以

式中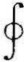表示沿循环路径的曲线积分。在循环中系统从外界吸收的净热量等于系统对外界作的净功。 因为

所以，系统对外作的净功为35kJ，系统从外界吸收的净热也是35 kJ。从这个简单的例子可以看出，不消耗外界任何能量而在循环中只对外界作净功的第一类永动机是造不成的。