热流道注射模设计计算时,必须具备传热学的基本知识,同时还要考虑温度升高时热流道系统零部件的热膨胀。塑料熔体流变学的基础知识前面已经介绍,这里讨论热流道系统的流道尺寸和喷嘴浇口的设计计算。
1.热传递
热传递有传导、对流和辐射三种方式,都影响热流道系统的热平衡。
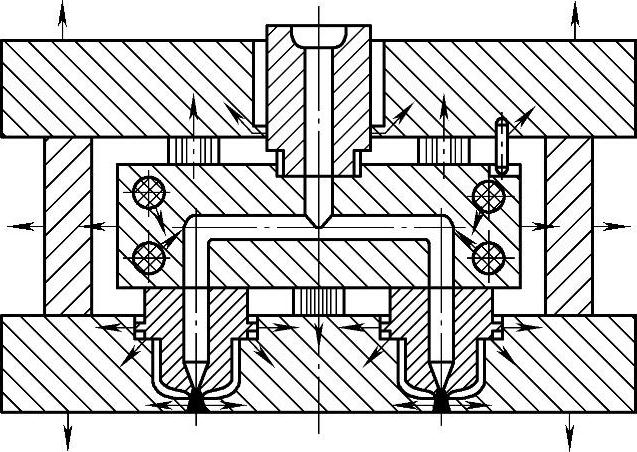
图12-17 注射模热流道系统的传导热流
(1)热传导 固体内部的热传导是由于相邻分子在碰撞时传递振动能的结果。金属的导热能力很强,因内部自由电子转移而发生。图12-17所示注射模的热流道系统的传导热流,其热源为流道板和喷嘴的电热功,还有注射生产中周期性输入熔融塑料携带的热量。热量主要从承压圈、喷嘴和联接螺钉等,经定模的接触面耗散。因空气的传热系数很小,定模框与流道板之间空气隙起绝热作用。空气、塑料和陶瓷常作为绝热材料。钢材根据不同的化学成分,其传热系数为14~40 W/(m·K),需根据各钢种实际测定。热流道系统零部件不但用各种合金钢制造,还用不锈钢和钛钢阻热,用铍铜导热。在热流道工程计算中,不考虑温度梯度随时间变化,只考虑位置温差的热传导。
根据傅里叶定律,物体存在温度梯度ΔT=T1-T2,传导热量Qc流过单层的平直模壁,如图12-18a上所示,可描述为

式中 Qc——物体的传导热量(W);
λ——材料的传热系数[W/(m·K)];
δ——物体传热方向的厚度(m);
Ac——物体传热面积,Ac=bh,(m2);
T1——热源温度(℃);
T2——被测点的温度(℃)。
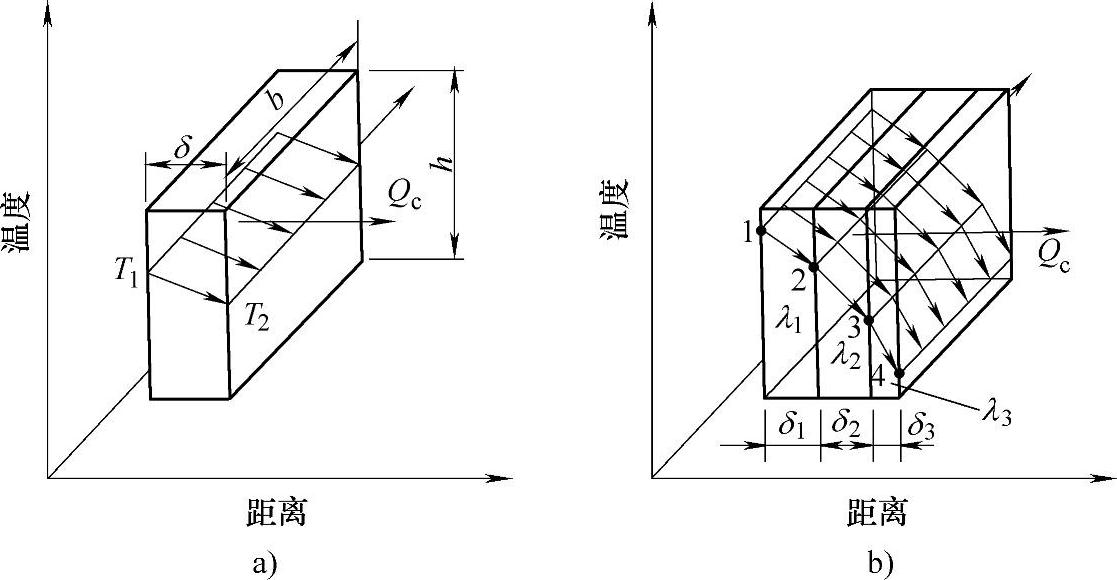
图12-18 单层和多层平壁的热量传导
a)单层物体 b)多层物体
多层物体的平壁热传导,如图12-18b所示可描述为
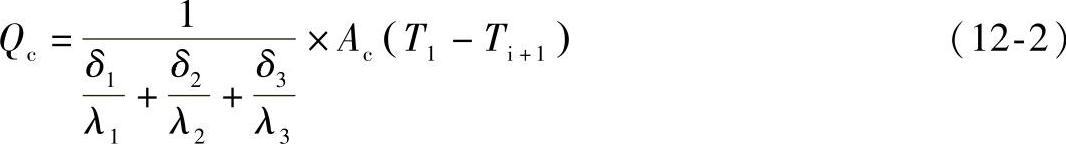
式中 i——物体间壁面的数量。
对喷嘴等圆筒形零部件,传导热量Qc流过单层的圆柱壁,如图12-19a所示,可描述为

式中l——圆柱壁面的长度(m);
ln——自然对数;
Ti——里筒壁温度(℃);
To——外筒壁温度(℃);
ro——圆筒外径(m);
ri——圆筒内径(m)。
传导热量Qc流过多层的圆柱壁,如图12-19b所示,可描述为
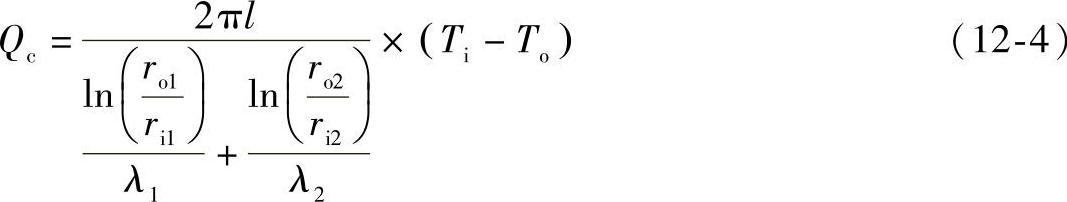
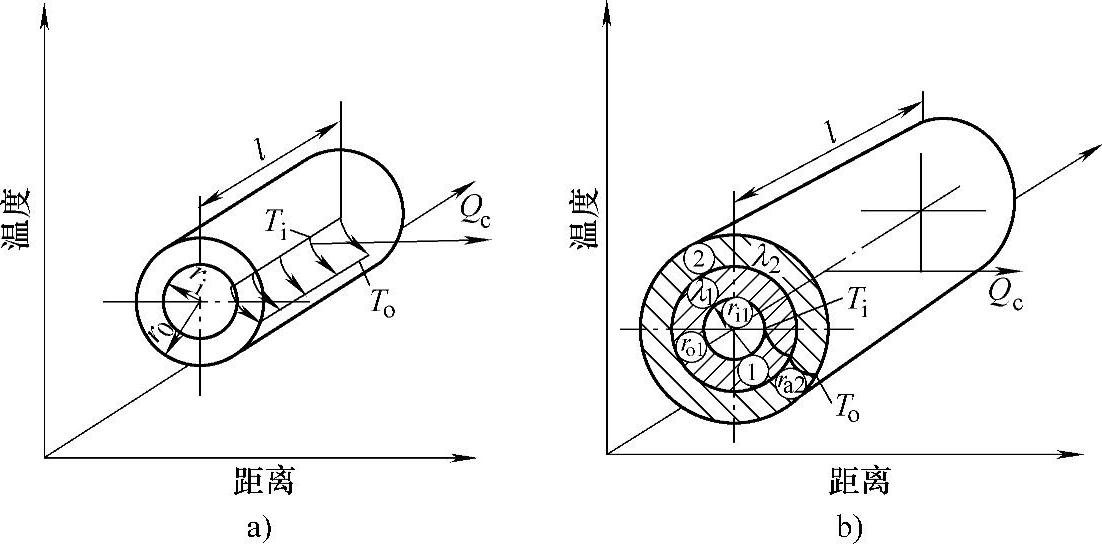
图12-19 单层和多层的圆筒的热量传导
a)单层圆筒 b)多层圆筒
式中ri2=ro1
例如流道板上的承压圈,可用不同材料组成的相关零件。如图12-20a所示,串联时的传热系数λs有

图12-20b上并联时的传热系数λp有
λp=φ1λ1+φ2λ2 (12-6)
以上两式中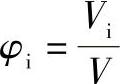 ;φ1+φ2=1其中φi——体积分数;
;φ1+φ2=1其中φi——体积分数;
Vi——单件体积;
V——总体积。
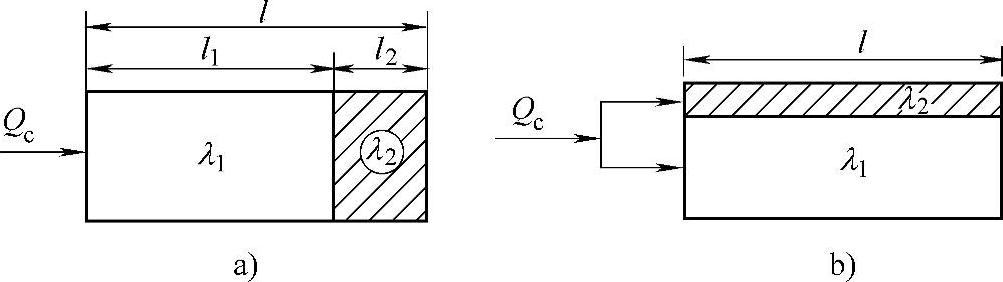
图12-20 不同材料两相关件的传热系数
a)串联联接的λs b)并联联接的λp
例如筒形的喷嘴在线圈外加热时,为多层圆柱壁串联的热传导。如图12-21所示的串联的传热系数λ r为

(2)热对流 在注射成型生产中,会遇到流体在流过固体表面时与该表面发生热量交换。从固体壁面到流体介质的热量传递称对流。图12-22所示为热流道注射模系统在注射生产中向空气的热对流。一方面流道板和喷嘴的壁面向周围的空气传递对流热量Q f;另一方面,定模框又向环境空气传递对流热量。在热流道工程计算中常用的是对前者的简化算法。加热后的空气变得更轻而向上自然流动。
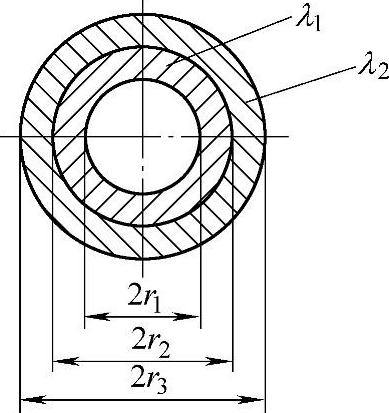
图12-21 多层圆柱壁串联的传热系数
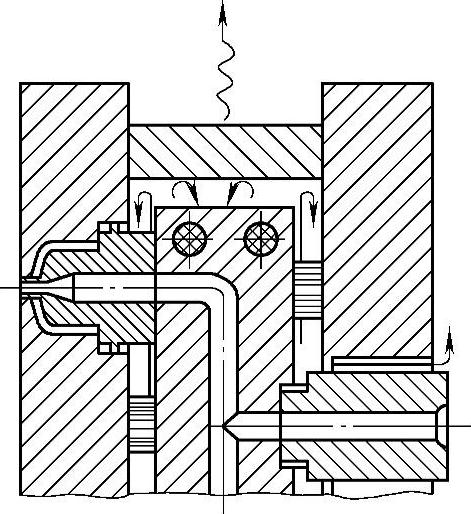
图12-22 热流道注射模系统向空气的热对流
如图12-23所示,平板壁面因空气的对流形成热量传递,这种对流热量
Qf=αfAf (TW-Tg) (12-8)
式中 Qf——对流热量(W);
α f——传热系数[W/(m2·K)],空气自然对流αf=5~10W/(m2·K);
Af——壁表面面积(m2);
TW——壁面的温度(℃);
Tg——周边环境空气的温度(℃)。
传热系数αf可以通过传热学理论计算,也可由理论指导下实验测得。如果是周边空气被强迫流动,传热系数αf=10~100W/(m2·K);而空气自然流动αf=5~10W/(m2·K)。曾有试验得到的αf值更小。先进的热流道板的绝热和反辐射措施很多,相应热传递计算在12.4节中进一步陈述。
(3)热辐射 任何物体都会不停地以电磁波形式向外界辐射能量。同时又不断吸收外界其他物体的辐射能。当向外辐射能与吸收能不相等时,产生的热量传递方式称热辐射。黑体的物质称为能吸收所有辐射能。可以假定辐射传递热量与通过的气体、液体和固体等介质无关。图12-24所示为热流道系统中热量的辐射传递,例如热流道板和周围的模板之间发生辐射能量的交换。流道板的保温设计,应让辐射能尽量多地反射回去。避免黑体效应,减少周围的模板吸收辐射能,这就要阻隔热流道系统与周围的模板之间辐射能的传递。
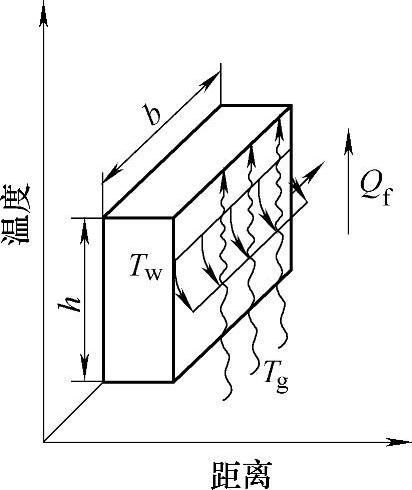
图12-23 平板壁面与空气的对流热量传递
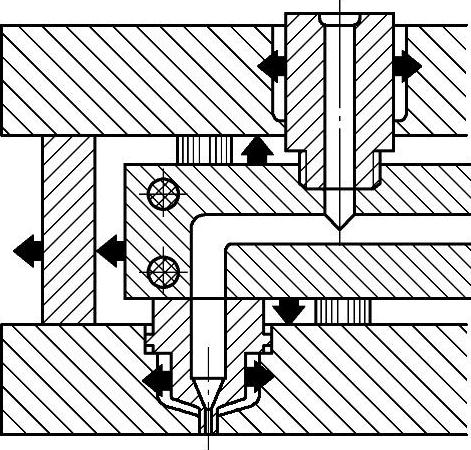
图12-24 热流道系统中热量的辐射传递
如图12-25所示两物体热量的辐射传递,高温平板表面向外界辐射能量Qr。这种辐射传热与传热系数αr的关系用下式描述
Qr=αr·Ar (T1-T2) (12-9)
式中 Qr——传递的辐射热量(W);
Ar——辐射表面面积(m2);
αr——传热系数[W/(m2·K4)];

式中 ΔT=T1-T2
T1——高温壁面的热力学温度(K),K=273+℃;
T2——低温壁面的热力学温度(K);
Co——热辐射系数[W/(m2·K4)]。
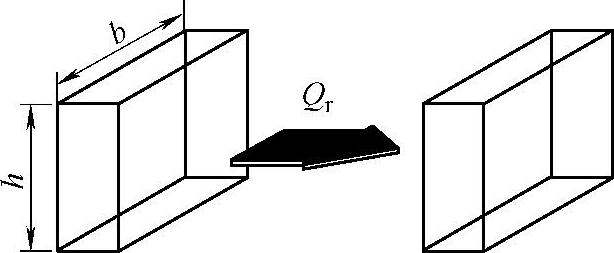
图12-25 两物体热量的辐射传递
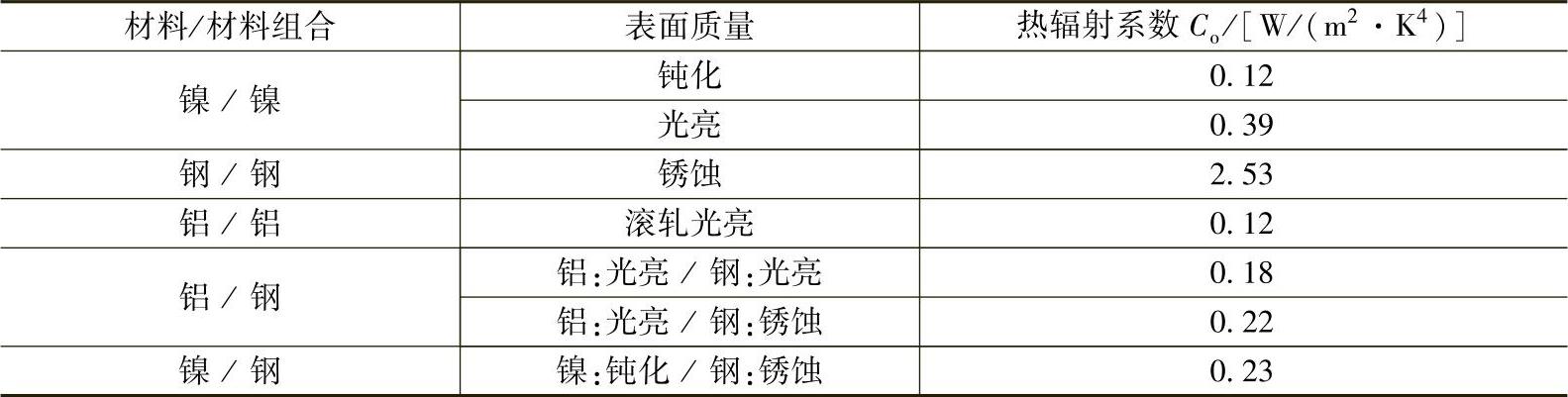
表12-3提供了热辐射系数Co与材料与物体表面状态之间的关系。为了使由热辐射引起的热损失最小,Co的值要小。为此,热流道板表面涂镍,Co=0.12W/(m2·K4)。流道板表面覆铝箔,Co=0.18~0.22W/(m2·K4)。详细措施在12.4节中介绍。
表12-3 不同表面质量和材料组合下的热辐射系数Co

(续)
2.热量和比热容
提高固体、液体和气体的温度要输入热能。所需的热量
Q=mCΔT (12-11)
工程设计时计算单位时间内输入物体的热量

式中 Q——输入热能(kJ);
P——物体加热功率(kW);
m——物体的质量(kg);
C——材料的比热容[kJ/(kg·℃)],表12-4;
t——物体的加热时间(h);
ΔT——物体温度升高值,ΔT=T1-T2(℃)。
比热容代表了物体材料的吸热能力。它表述1kg单位质量的物体,温度升高1℃所需的热量。还需注意到比热容还与温度有关。
由两种材料组分组成的物体的相当比热容Ctotal计算如下
Ctotal=φ1C1+φ2C2 (12-13)
φ1+φ2=1
式中

mi——单个组分的质量(kg);
mtotal——装配体的总质量(kg)。
表12-4 一些固体、液体和气体的比热容C

3.热膨胀
对于注射模热流道工程,只需要考虑线性热膨胀。物体某个方向在热影响下尺寸的变化,取决于温度梯度ΔT和材料的线性热膨胀系数α。有
ΔL=L1-Lo=αLo ΔT (12-14)
式中 ΔT=T1-To
α——线性热膨胀系数(1/K),见表12-17;
Lo——在参考温度To(=23℃)时的长度(m);
L1——在测量温度T1时的长度(m)。
线性热膨胀系数等于物体沿长度方向上的相对伸缩量与温度梯度的变值(https://www.xing528.com)

各种材料的线性热膨胀系数随着温度的上升而有所提高。金属和塑料材料的线膨胀系数较大,而且升温时变化较多。因此在金属物体的热膨胀计算时,在介于环境温度和工作温度之间取线膨胀系数值。表12-17给出的大都是室温下的线膨胀系数。
受到机械约束的零件,受阻挡的热膨胀会导致热应力
σ=εE (12-16)
式中,E为材料的弹性模量。式中应变

由式(12-14)和式(12-15)至式(12-17),可得到热应力
σ=αE (T1-To) (12-18)
被约束的受热钢零件,有弹性模量E=2.1×105 MPa,线膨胀系数α=11×10-6/K。ΔT=260K。计算得到很大的热应力σ=600MPa。在热流道板的设计时,必须给出室温下的补偿间隙。以防止破坏相关的零件,详见12.4节。
为了改善热流道板和喷嘴的导热性,常在钢构件中嵌入铍铜。这时的热补偿,见图12-26所示。要将不同材料物体作为静力系统。作用力F按比例作用在两个相同长度L的零件上。两零件在F1、F2约束下的变形量f1、f2相等,称为变形协调条件,见下式

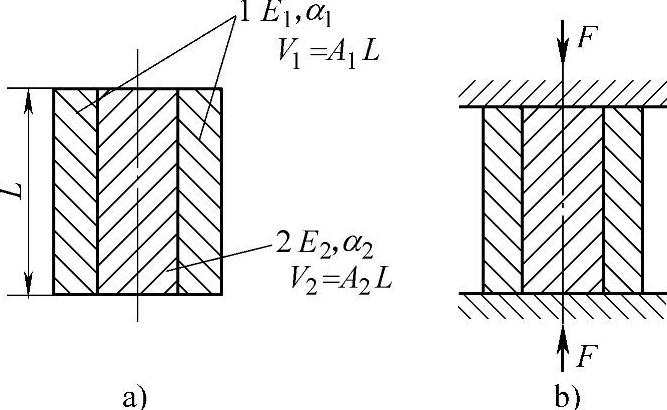
图12-26 两种材料物体热膨胀时的变形补偿
a)两种材料组合 b)对热膨胀的约束力F
如图12-26a所示,两种材料物体各有其物理性能E1、E2、α1、α2。各有几何参数,其体积V1=A1 L,V2=A2L,A为物体的截面积。由以下式
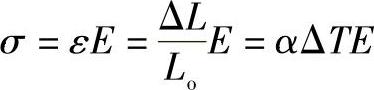
和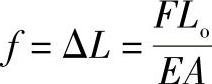
定义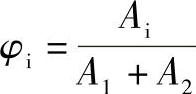
可得到两种材料组合结构的线膨胀系数

4.系统的热流道尺寸设计计算
在一模多腔热流道注射模的流道板上,流道的布置和截面尺寸的设计,必须实现注射的塑料熔体对各型腔平衡充模,以保证注射制品的质量和精度的一致性。本节介绍流道系统的分类和设计原理,举例说明流变平衡计算流道截面尺寸的方法。
流道系统包括主流道喷嘴、各分流道、浇口喷嘴。为保证各注射点的熔体充填型腔时的压力,整个系统的熔体流动状态的压力降应控制在30~35MPa。本节仅讨论流道部分的设计。
有两种多型腔模具的流道平衡设计。
图12-27所示是自然平衡的流道布置。从主流道喷嘴到各浇口喷嘴的流动距离相等。只要对称布置的对应分流道的圆截面半径相同,就可以实现各浇口喷嘴的平衡浇注。
图12-28所示是不平衡的流道布置。从主流道喷嘴到各浇口喷嘴的流动距离不相同。不同的流程压力会造成各注射点的熔体充模压力的差异。但经流变平衡计算,调节各分支流道的半径,也可以达到各浇口喷嘴的平衡浇注。
由于流道的流程与塑料制品型腔可分开处理,这两种流道可以人工计算设计,也可以编制计算机程序计算,流道的平衡设计,要在一定的熔体温度下,以最佳的剪切速率和允许的压力损失流动充模。
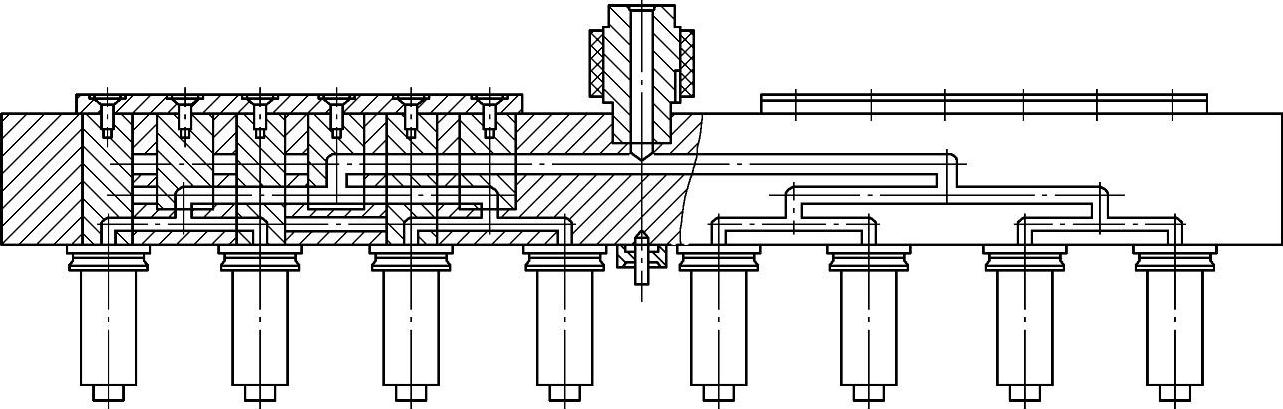
图12-27 热流道系统自然平衡的流道布置
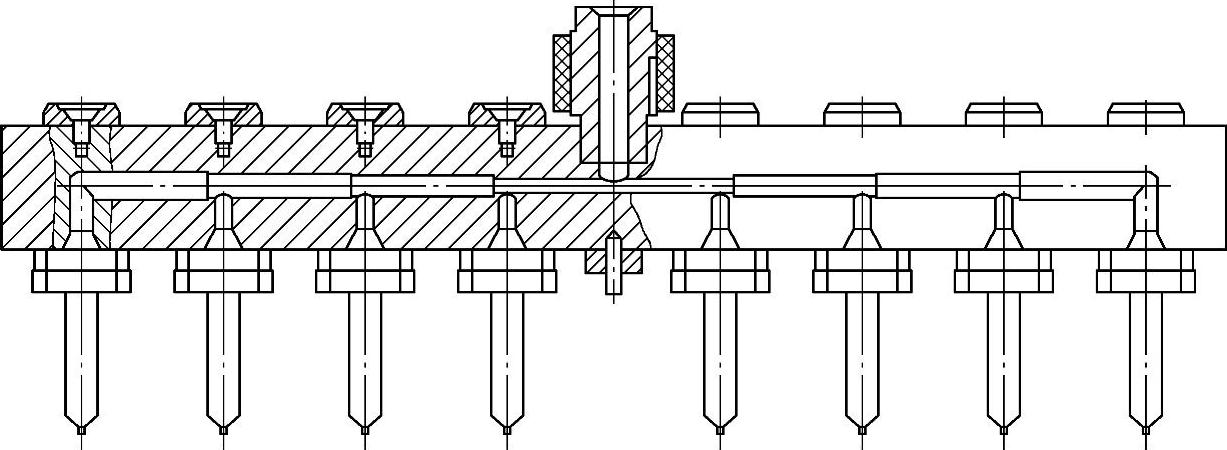
图12-28 热流道系统流变平衡的流道布置
参照图12-27的自然平衡流道布置,与图12-28的流变平衡流道布置相比。前者的熔体流动距离长,流道的分叉转折多,流道板厚且结构复杂。后者结构简单,但流变平衡计算较为困难。
此外,对于不同制品的多型腔模具,例如塑料盒和盖两者在一个注射模中成型的流道设计,要求熔体同时充满各个型腔。对于单个大型型腔,例如轿车的保险杠,有多个注射喷嘴浇注。此种流道设计时,要考虑熔体料流前锋的运动状态,要保证熔合缝处于合理位置。这些制品型腔的平衡浇注,须将浇道系统与型腔一起,经电子计算机造型,进行流动模拟分析,经反复修正达到流变平衡充模。
(1)自然平衡布置流道尺寸计算 图12-27所示的自然平衡布置的流道截面,同样要以流变原理进行直径大小的计算。在熔料熔融的中间温度下,以适中的螺杆推进速率,计算注射熔料在流道中的剪切速率与剪切应力,预测表观黏度,估算流道全程的压力降。这个计算过程的依据是各种塑料熔体的流变曲线。塑料熔体的非牛顿特性是剪切速率升高时表观黏度下降,流动性改善。过分大的流道直径,使熔体流动的剪切速率较低,表观黏度上升。况且,如果制品型腔很小,而流道的容积较大,会延长熔体在流道中的停留时间。这对于热敏性的物料,例如PVC和POM及一些添加阻燃剂物料,它们在料筒和热流道中停留时间超过5~10min会产生分解和挥发;反之,过细的流道直径会使压力传递困难,造成熔体充模压力不足。因此需反复计算,调节流道直径,使主流道喷嘴有1000s-1以上的剪切速率;各流道中有剪切速率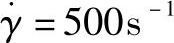 左右。各种塑料流动熔体的表观黏度大致为100~500Pa·s。下游的浇口喷嘴的熔体有更高的剪切速率和更低的表观黏度。
左右。各种塑料流动熔体的表观黏度大致为100~500Pa·s。下游的浇口喷嘴的熔体有更高的剪切速率和更低的表观黏度。
为了使多型腔模具实行平衡浇注,采用图12-29所示的注射点的布置方式。一类是2n方式(2、4、8、16和32)的型腔对称的等路径布置。另一类是3的倍数方式,常用3、6、9、12和24个型腔的等路径布置。
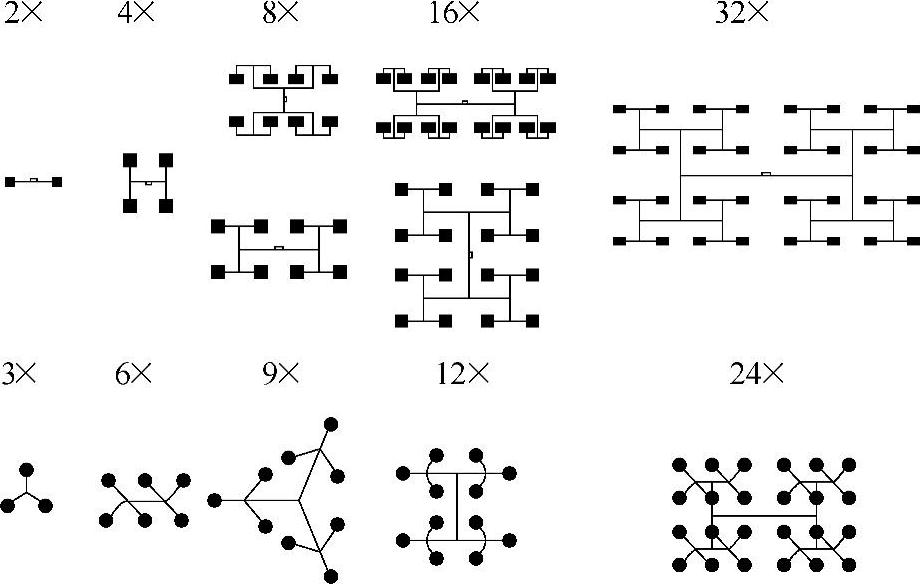
图12-29 常见的一模多腔的自然平衡布置
在多层次的分流道直径计算时,推荐用下式
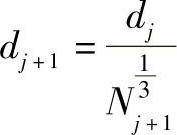
式中 dj——上游流道的直径(cm);
dj+1——下游流道的直径(cm);
Nj+1——下游流道的分支数。
参照前第8章泠流道尺寸的设计计算方法,如图12-27所示流道,经流变计算得第一分流道直径d1=1cm;则第二分流道直径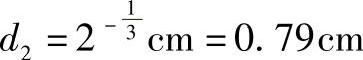 ;第三分流道
;第三分流道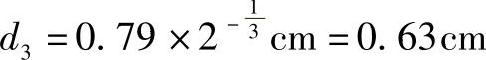 。根据此直径分配式的计算结果,各层次的分流道中熔体的剪切速率递减,而剪切应力大致相等。
。根据此直径分配式的计算结果,各层次的分流道中熔体的剪切速率递减,而剪切应力大致相等。
(2)非平衡布置的流变平衡计算 图12-28一模八腔的热流道注射模,注射POM每件3cm3手柄制件。熔体的注射温度定为200℃。按注射工艺常见的螺杆推进速率,确定注射充模时间为0.5s。对热流道模具的每次注射体积,应不计流道系统的容积,有V=3×8cm3=24cm3。按合理的剪切速率γ·=478s-1,确定第一分流道直径d1=0.8cm。图12-30为流道的布置和流变平衡计算得到的结果。
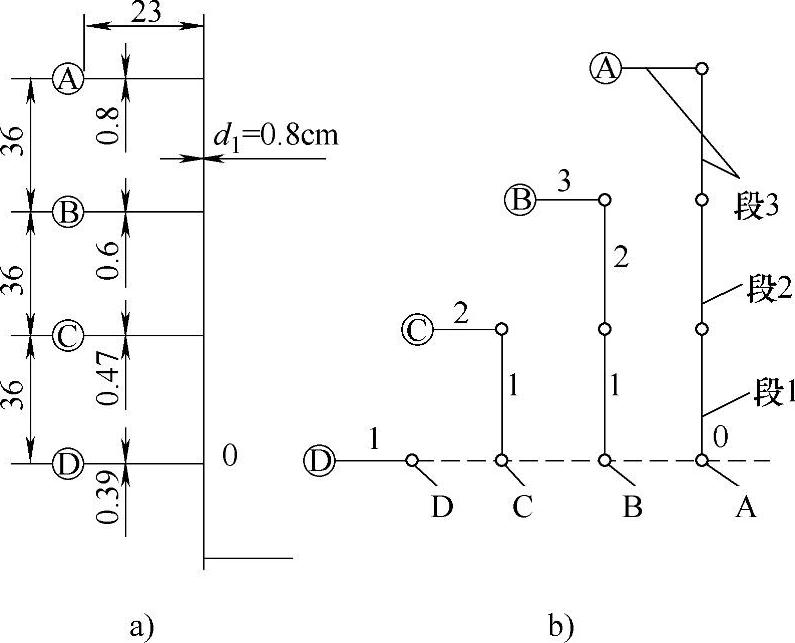
图12-30 八个型腔的流道的布置和流变平衡计算结果
a)型腔分布和流道直径计算结果 b)流程的计算分段
如图12-30b所示,流道系统的一半被分解成四个流程。又将每个流程分成若干个计算段。从计算0点起,流程D仅有一段;流程B有三段;流程A是等直径d1=0.8cm的三段。不计流道中熔体的体积,通过A流程1段的熔体体积为3V/8。通过A2段的体积为2V/8;流过A3段的体积为V/8。计算各流程各段的压力降见表12-5。流程A有2.3+1.7+1.7=5.7MPa压力降。流程B中B1和B2段,与A1和A2段一致,为3.6cm。为实现流变平衡,B3段与A3段应有相同的压力降。也就是B3段的2.3cm长有较细的直径,与A3段(2.3+3.6)=5.9cm长,直径0.8cm有相同的1.7MPa压降。经计算得B3段直径为0.6cm时,可实现平衡浇注。
表12-5 一模八腔热流道的流变计算结果
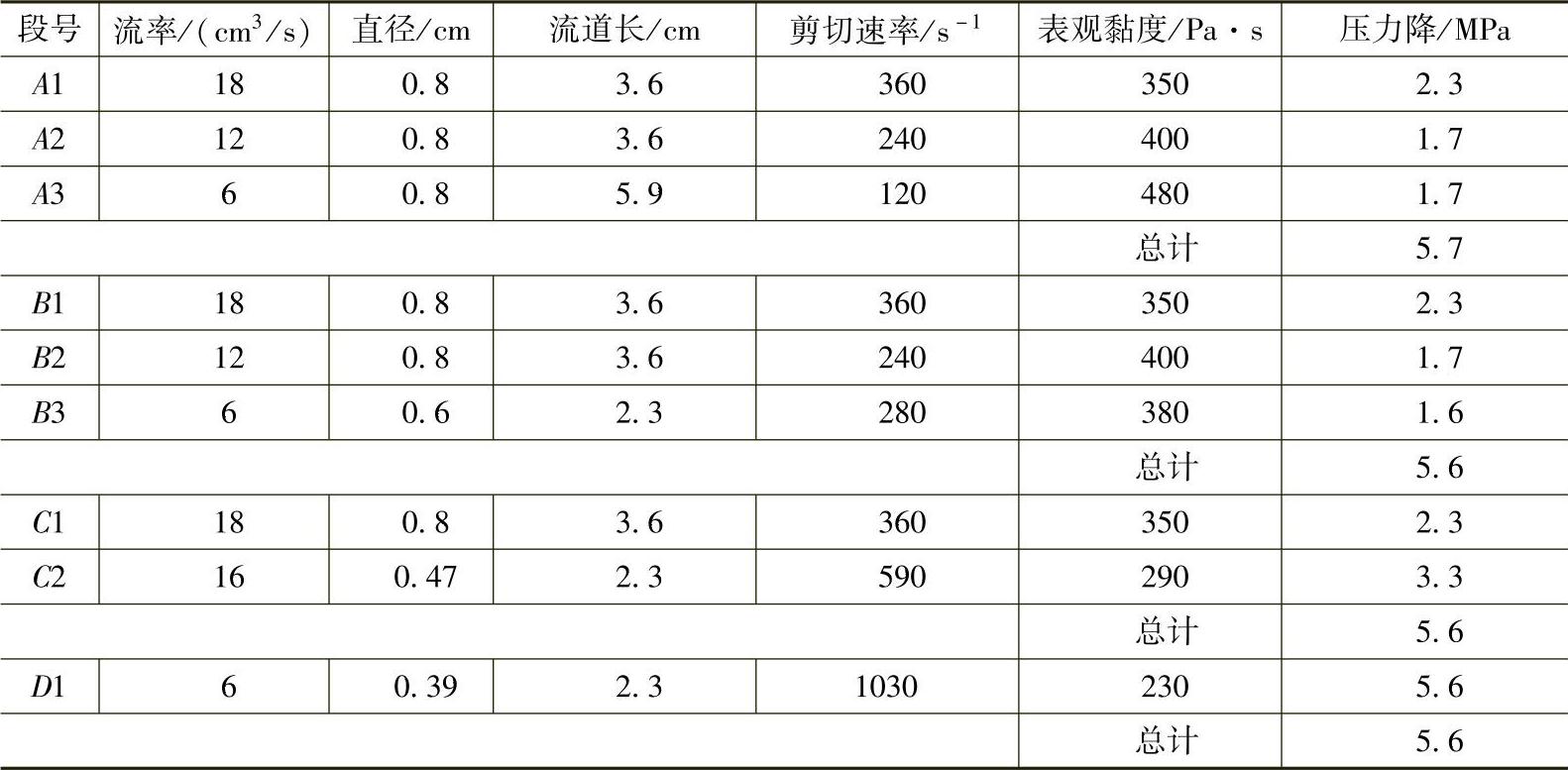
现以B3段为例,说明流变平衡计算的原理。首先计算B3段的体积流率
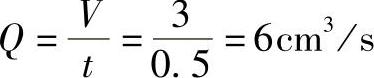
式中 V——流过流道的熔体体积(cm3);
t——注射时间(s)。
注射50cm3熔体体积的注射时间为1.5s;注射50~250cm3需1.5~2.5s。又有B3段中熔体流动的剪切速率
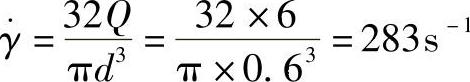
式中d为此段流道的直径(cm)。在POM的表观黏度ηa—剪切速率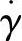 的流变曲线图12-31上,在熔体温度200℃曲线上,查得ηa=380Pa·s。由此得B3段的压力降
的流变曲线图12-31上,在熔体温度200℃曲线上,查得ηa=380Pa·s。由此得B3段的压力降
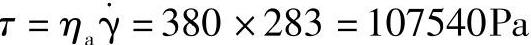
有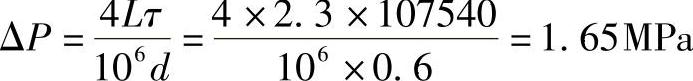
式中 τ——通过流道的熔体剪切应力(Pa);
L——该流道的长度(cm)。
较高的熔体温度和较短的充模时间,都能改善塑料熔体的流动性,有利充模压力的传递。在注射生产中,可参考平衡计算中设定的温度与时间进行调节。
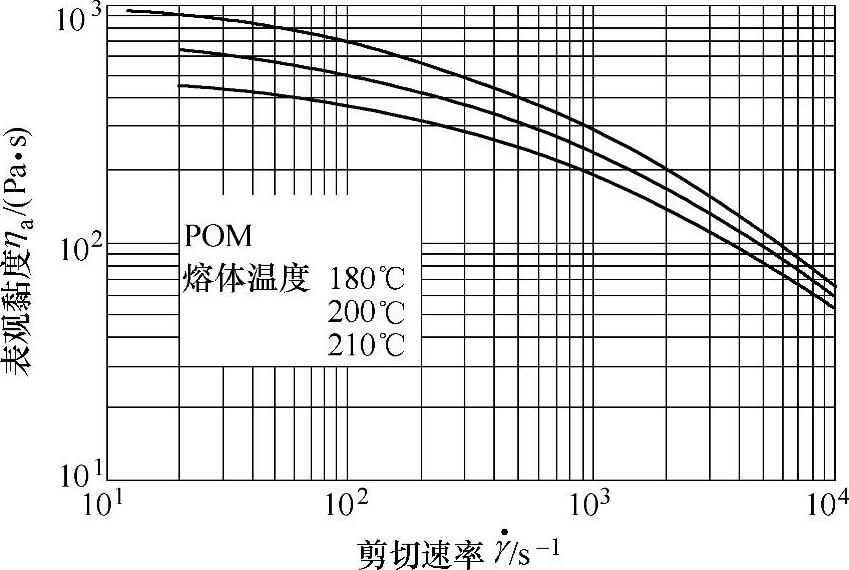
图12-31 共聚甲醛POM的流变曲线
5.喷嘴流道的设计计算
喷嘴有种类的选择和喷嘴流道直径确定的两方面。喷嘴流道的较小传输截面积,会使流道中的压力损失增大。在一定的注射压力下,使注射到型腔的熔料因充模压力过低,而达不到所需的充模速率,会影响注塑件质量,甚至使型腔不能充满。较大的截面面积将会增加浇注系统用料和能量损耗,增加熔体塑料在高温流道和喷嘴中的渡过时间。这里介绍用流变学原理和方法,计算确定喷嘴流道直径。但是在喷嘴长度超过100~200mm时,还需校核整个热流道浇注系统的压力损失不超过350MPa,为此有时不得不放大喷嘴流道的直径。
(1)喷嘴流道直径计算式 以合理的剪切速率,又考虑塑料熔体的黏度,计算确定热流道系统的喷嘴流道直径。计算公式源于塑料流变学,依据各种塑料熔体的非牛顿性能,可获得正确的结果。
热流道系统的喷嘴内径尺寸,由材料的流动指数n、剪切速率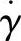 以及注射的体积流量共同决定。此流量qi为喷嘴注入下游型腔的体积流量,可由该喷嘴射出注射量和注射时间计算
以及注射的体积流量共同决定。此流量qi为喷嘴注入下游型腔的体积流量,可由该喷嘴射出注射量和注射时间计算
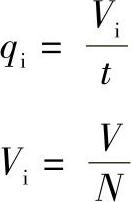
式中qi——分流道的体积流量(cm3/s);
t——对下游型腔的充模时间(s);
Vi——单个喷嘴的注射量(cm3);
V——注射模型腔的总体积(cm3);
N——流道分叉数。
在浇注系统的圆管流道中,各截面的熔体充模时间t是相同的。在已知以上数据的情况下,按剪切速率确定喷嘴内流道直径,可由前流变学公式(8-2)计算得
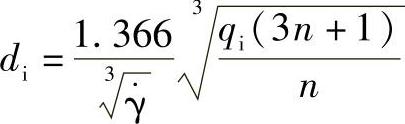
式中 n——塑料熔体的流动指数,可参考前表2-1或表2-2;
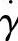 ·——塑料熔体的合理剪切速率(1/s)。
·——塑料熔体的合理剪切速率(1/s)。
(2)充模时间的确定 热流道喷嘴是热流道系统的终端,它将熔料输送到模具型腔或附加的冷流道。在喷嘴直径的计算过程中,模具型腔总体积V通过以下注射量和时间的关系确定注射时间t。该注射时间t是根据注射机螺杆的常规推进速率。即注射机具有中等注射速率时,相对应的注射充模时间。表8-1是注射机常规注射速率下,对应的充模时间和公称注射量关系。大量工程计算证明,此方法能正确确定浇注系统流道中熔料的充模流量。也能适应注射机操作对充模速率的调节。
将表8-1的数据经多项式拟合的式(8-1c),在编制计算机程序时分成两段,对注射量30≤V(cm3)<2500
t=0.8998+0.37902×10-2 V-0.17210×10-5V2+0.28900×10-9 V3
当注射量2500≤V(cm3)<64000时
t=0.34115×10+0.44075×10-3 V-0.77653×10-8V2+0.49935×10-13 V 3
式中 V——注射量(cm3);
t——注射时间(s)。
(3)合理的剪切速率 大量的注射成型的实验和计算机模拟数据证明,浇注系统各流程,从主流道、各分流道到喷嘴内径,存在合理的剪切速率的范围,见表12-6所示。塑料熔体有较高的黏度,较高温度下黏度较低些。塑料熔体另一个特性是非牛顿性,有“剪切变稀”的现象。在圆管中剪切流动时,剪切速率高,熔体的黏度下降明显。而剪切速率主要与流道截面内的体积流量有关。因此,热流道系统上游的主流道喷嘴、中游的各分流道,下游的分喷嘴,有不同的合理的剪切速率范围这有利于降低黏度,减小沿程的压力损失,保证对成型型腔成功充填。
表12-6 热流道多喷嘴系统各流程合理的剪切速率

图12-32 贮物箱
(4)应用示例 图12-32所示贮物箱,箱体面积540mm×210mm,高220mm,壁厚3~4mm。箱体用3640cm3的ABS塑料注射成型。有四个某型号顶管式的,浇口在模板的喷嘴。喷嘴的总长102mm,管径16mm。图12-32为浇注系统设置为保温的热流道做的流动分析。6.056s是塑料熔体总体积充满时的状态。其中热流道中熔体的流动充模时间在5s之内。用Lustran ABS 1146物料,熔体温度260℃。
每个喷嘴的射出量为910cm3。由总注射量3640cm3,查表8-1得可行的充模时间t=4.8s,得流经喷嘴流量qi=190cm3/s。又按表12-6,开放式多喷嘴,在较大流量下,应具有合理的剪切速率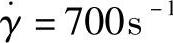 。查表2-6,Lustran ABS 1146物料在102~103s-1下,熔体的流动指数n=0.346,代入式(8-2)得
。查表2-6,Lustran ABS 1146物料在102~103s-1下,熔体的流动指数n=0.346,代入式(8-2)得
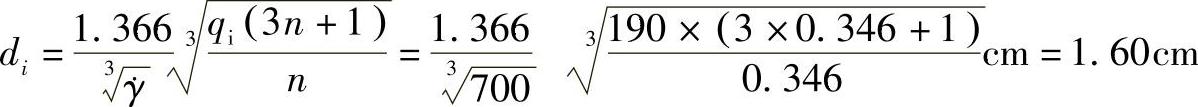
考虑到注射生产时,还允许调节注射充模和剪切速率,且归整到喷嘴直径的系列尺寸,故用流道直径为16mm的多喷嘴。
6.以塑料流动性和注射量选定浇口直径
塑料熔体流经喷嘴浇口的剪切速率要比分流道中约高10倍,充分利用非牛顿流动特性,改善流动性。表12-7列出喷嘴的各种浇口的合理剪切速率。同样用式(8-2)计算浇口直径。以合理的剪切速率,又考虑塑料熔体的黏度,计算确定的喷嘴的浇口直径。但是考虑到顶针式浇口中,鱼雷顶针尖的阻塞和热传导的作用,塑料熔体是在圆环隙管道中剪切流动,流变学计算公式复杂。又根据PSG Plastic Group Gm-bH公司资料,分喷嘴顶针式浇口流经PP、PA和ABS等黏度较低物料,合理的剪切速率范围为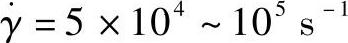 。对PC、PMMA和PVC等黏度较高物料,合理的剪切速率范围为
。对PC、PMMA和PVC等黏度较高物料,合理的剪切速率范围为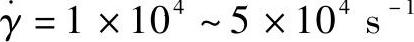 。
。
表12-7 各种喷嘴浇口的合理剪切速率

[例]某PC塑料制品的质量为m=50g,PC密度为ρ=1.2g/cm3,流动指数n=0.67。制件为半径r=45mm、高h=40mm、壁厚为s=1mm的圆筒形容器,设计计算分喷嘴顶针式浇口直径。
[解]①计算充模流量
型腔体积为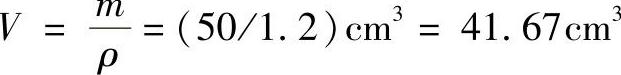
按表8-1查得注射量60cm3的中等充模时间为1s,注射量30cm3的充模时间为0.86s,用线性插值,由下式计算型腔体积V=41.67cm3时的充模时间
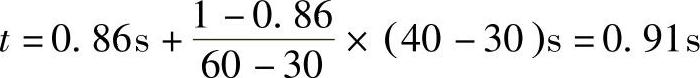
通过浇口的流率为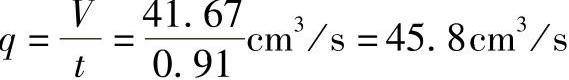
②计算浇口直径
由表12-7查得流经分喷嘴顶针式浇口的合理剪切速率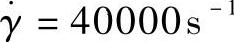 ,代入式(8-6)得
,代入式(8-6)得
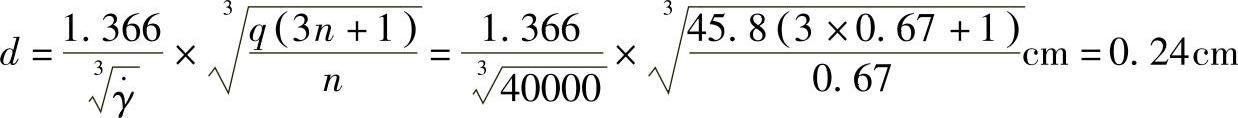
初步计算得浇口直径为2.4mm。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




