系统网络早期概算注射模具成本分析

注射模具的零部件设计和制造的成本评估，要比注射加工注塑件困难得多。这是由于设计注射模具本身就是项艰巨的任务，影响模具成本的因素是多维的。成本和这些因素之间关系也是复杂和非线性的。因而，如果不能发展基于数学及科学原理的精确分析模式，将会是十分困难的。另一方面，模具行业非常希望有个精确的计算机模式，快速地完成模具成本概算。成本函数的近似处理方法，必将成为发展注射模具成本早期概算的工具。

系统网络的成本函数应用了近似引导方法。它根据制品设计所涉及模具制造工艺的成本的关系，并以模具加工实际构成为成本的组分。参照注射制品与模具成本的历史数据，处理设计成本与制造成本有关的因子之间的近似关系。

在本节中，首先介绍成本函数用于系统网络的处理方法；然后按模具零部件设计及其与制造关系，识别成本因子，陈述历史资料和成本数据的使用，了解近似的成本函数使用系统网络的过程。

1.应用系统网络的近似成本函数

成本函数近似处理方法中主要有两个阶段。首先是数据准备阶段，定义成本函数的变量，并收集历史数据。第二阶段，系统网络的近似函数建立和使用。

（1）定义成本函数的变量 数据准备，定义成本函数变量的步骤如下。

1）塑料制品/模具零部件的邻域需要定义。常定义整段时间的某公司生产的制品/零部件，应选择在材料成本和制造技术/业务关系稳定的时间段。

2）在设计工作中需要确立所有成本关系因子（cost-related factors，CFs）。定义邻域内所有制品/零部件，都应确定成本关系因子CFs。

3）每个CFs的数量都要建立量化方案。有两种类型的CFs。第一种是连续的数量值。它能被简单的规准量化。第二种是设计变量，一般没有任何数值被分配到每个需量化的变量。通常，依照成本因子CF的各个成本花费的不同状态，指定数值并不按比例关系。要求量化方案对每个成本因子CF的所有状态都要考虑。

4）收集历史成本数据。个案进程和范例的选择能有效用于近似函数。因此，前期生产制品/工件的工艺资料全部编入范例中。对于每个选择的范例，它的成本因子CFs被摘取和量化。活动性成本用于故障处理，最终建立起一系列活动成本的{CFs}函数。

在这一阶段结束后，应收集了一套完整的范例。每个范例点都需要设置许多（CF₁，CF₂，…，CF_n）→成本。设定n为CFs总数。

建立数字化范例后，在（CF₁，CF₂，…，CF_n）和成本之间设立近似函数有不同方法。这种回归方法是对近似函数的传统处理方法。通过历史数据回归分析，获得系数和指数。然而，成本和CFs之间的非线性关系是未知的，这就必须作些假设。

（2）系统网络的近似函数 人工神经系统网络（artificial neural networks，NN）是使用计算机模仿生物神经系统的信息化技术。NN的重要应用之一是可用于不明确输入与输出关系的系统模式中。通常，系统没有精确的信息，仅能研究已有实际系统的有用范例，并使网络认识它。给出固定的人工网络，用随机梯度方法，使之执行网络参量的修改，最终使损耗函数确实最小。在各种NN中，逆向传输NN（back propagation NN，BP-NN）从一些范例认识输入与输出的关系，适用于近似函数。

在BP-NN中有输入层和输出层，在它们之间有一个到几个的隐藏层。每层都有许多过程单元，称为神经元。图6-10所示的三层BP-NN系统，只有单一输出、加权的输入和经神经元计算，再从总和减去它的临界值，并且经转换函数运算后输出结果，可用下式表达：

式中，x_j为当前的输入，y_i是最终的神经元的输出，w_ij是与x_j相关联的加权数，s_i为各神经元的临界值，f_i是转换函数。w_ij的值决定了输入对神经元的影响有多强。在试算过程期间，权重的数量值能改变。它主要通过神经元适应新信息的机理，完成认识过程。BP-NN参照了它们的试用算法（training algorithm），获得误差的逆向传送。这个网络开始试用时，指定所有权重的随机值，随后输入当前网络，然后从每层上的每个神经元，经过整个网络向前传送，影响实际的输出。将实际输出和它对应的目标输出估算出差异，作为输出层中每个神经元的误差。这个误差经过整个网络返回传送，在专门的神经元中，按差错的直接比例，调整联接单元的权重。通过这种网络方法减少误差。由于对每个输入范例的输出目标是已知的，所以这个试算过程也称控制试算（supervised training）。

图6-10 三层BP-NN系统

在NN的认识阶段，应设置误差的允许范围，作为停止试算的临界值。一旦试算完成，NN设定了最终的权重和偏差，代表了近似的成本函数。给出新的制品/零部件后，先做CFs提取和定量，然后输入给NN，完成成本概算。

2.注射模的成本相关因子

与成本相关的因子CFs影响着模具的成本。这些因子包括模具零部件的技术要求。它从客户的要求而来，又有基于设计者提出的要求。举例说，零部件规格包括注塑件的尺寸、质量和公差、支承类型和数量、肋和凸台。同样也有相关模具零件的结构、装饰花纹及表面粗糙度。概念化模具设计的技术要求包括型腔的数目、分型面的形状。注塑件外侧或/和内侧凹凸槽，也对应着一些滑块或/和斜顶杆的需要。

成本相关因子CFs的确定，主要参照模具报价、有经验的设计和制造工程师的意见。现有下列19个CFs已经被定义，这些因子被量化，将它们的作用状态，用0到1之间的数值设置到每个CF。CFs和它们的量化设计陈述如下。

1）型腔的数目，N。决定于概念化的模具设计阶段。型腔的数目越多，模具的价格就越高。设定公司制造模具型腔的最大数目为16，有CF₁=N/16。

2）注射制品质量。假设公司的最大质量制品为2000g，则有CF₂=W/2000。

3）制品在分型面上的投影面积，A/cm²。投影面积的越大，会增加型芯和型腔板，及模架的成本。假设本公司的制品有最大投影面积30000cm²，则CF₃=A/30000。

4）开模方向的模具高度，H/cm。模具高度越大，会增加型芯和型腔模板的成本。假设本公司的模具最大高度H为30cm，CF₄=H/30。

5）模具的类型。模具的四种类型和与它们相应的CF₅如下。

①冷流道两板模，CF₅=0.1；

②冷流道三板模，CF₅=0.13；

③单喷嘴热流道模具，CF₅=0.2；

④多喷嘴（2～6）热流道模具，CF₅=0.5。

6）分型面的类型。分型面分离动模和定模。越复杂的分型面，加工的成本就越大。下面给出了分型面的六种类型和与它们相对应的CF₆。

①平面分型，CF₆=0；

②单个阶梯平面，CF₆=0.3；

③单个的阶梯平面或简单曲面，CF₆=0.5；

④多于四个的阶梯平面，CF₆=0.63；

⑤复杂的曲面，CF₆=0.75；

⑥有阶梯的复杂的曲面，CF₆=1。

7）定模上滑块机构的数量，。滑块机构垂直开模方向，从注射制品外侧凹槽中抽出。滑块机构组装到型腔，需要液压力来抽拔，因此增加了成本。假设在模具型腔上滑块机构的数量最多为2，则有。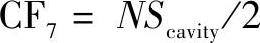

8）动模上滑块机构的数量，。比起在定模上的滑块机构，此种滑块机构的成本较低。机构由斜导柱和弹簧作用抽拔成型零件。然而。增加滑块机构的数量，一定会增加模具的成本。在模具中滑块机构最大的数量为12，有。

9）内侧抽机构的数量，N。内侧抽机构斜顶杆沿着开模方向，在注塑件的侧凹槽上抽拔。模具中增加内侧抽机构的数量，会增加模具的成本。模具中内侧抽机构的最多数目为4，则有。

10）小型内侧抽机构的数量，模具中的小内侧抽机构的最多数目为8，CF₁₀=。

11）表面粗糙度。提高对模具成型表面粗糙度的要求无疑会增加成本。下面列举的表面粗糙度要求和与之对应的CF₁₁值。

①无要求，CF₁₁=0.1；

②标准无光泽，CF₁₁=0.15；

③不反光低粗糙度，CF₁₁=0.2；

④镜面低粗糙度，CF₁₁=0.3；

⑤最低粗糙度，CF₁₁=4。

12）装饰雕刻。模具有三种常见的装饰雕刻类型：普通凹字，隆起文字或商标，模内标签和图形。CF₁₂定量如下所述。

①没有雕刻，CF₁₂=0.1；

②普通刻凹字，CF₁₂=0.2；

③隆起文字或商标，CF₁₂=0.5；

④模内标签和图形，CF₁₂=0.7。

13）型芯的结构。若在动模一侧，CF₁₃=0.2；另外方式，CF₁₃=0.1。

14）型腔的结构。若在定模一侧，CF₁₄=0.2；另外方式，CF₁₄=0.1。

15）制品上的尺寸公差。塑料制品尺寸公差的要求，对模具制造过程和加工成本有着很大的影响。这是因为模具制造者按很小公差制造模具。它只是经模塑过程余留下来的公差带。下面给出的CF₁₅定量。

①大于±0.5mm，CF₁₅=0.01；

②近似±0.35mm，CF₁₅=0.07；

③近似±0.25mm，CF₁₅=0.17；

④近似±0.20mm，CF₁₅=0.33；

⑤近似±0.1mm，CF₁₅=0.67；

⑥近似±0.05mm，CF₁₅=0.8；

⑦近似±0.03mm，CF₁₅=1.0。

16）制品上的肋。肋的存在会增加模具的制造成本。以塑料制品上肋的大致数量和类型，CF₁₆的定量如下所述。

①没有肋，CF₁₆=0.1

②高度﹤10mm为低的，和﹤5条是少的，CF₁₆=0.12；

③高度﹤10mm为低的，和﹥5条是多的，CF₁₆=0.15；

④高度﹥10mm为高的，和﹤5条少的，CF₁₆=0.17；

⑤高度﹥10mm为高的，和﹥5条多的，CF₁₆=0.4。(www.xing528.com)

17）制品上的装饰。存在装饰会增加模具的制造成本。按装饰的大致数量和类型，CF₁₇的定量如下所述。

①没有装饰，CF₁₇=0.1；

②深度﹤1mm为浅的，和﹤5片是少的，CF₁₇=0.12；

③深度﹤1mm为浅的，和﹥5片是多的，CF₁₇=0.15；

④深度﹥1mm为深的，和﹤5片是少的，CF₁₇=0.17；

⑤深度﹥1mm为深的，和﹥5片是多的，CF₁₇=0.4。

18）脱模顶出机构类型。共有四种不同的类型，会导致不同的成本。CF₁₈定量如下。

①顶杆脱模，CF₁₈=0.1；

②片条顶出，CF₁₈=0.2；

③板块顶出，CF₁₈=0.35；

④双脱模，CF₁₈=0.5。

19）液压缸的数目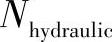。液压缸的使用会额外增加模具成本。模具中液压缸数量最多为4，则有。

以上CF的类型，在电子产品的模具制造中得到了认同。以公司先前的模具生产作为量化因子基准，对其他类型模具进行成本概算时，这些因子应该被重新验证。标准化的因子要重新定义。

基于上面CF的定义，对92副生产模具的零件进行检验，并提取它们的CFs。依照制造数据，计算了它们对应模具的实际成本。这些成本值乘以常数因子，保证了真实性。92套CFs的设置和成本数据，列于表6-23中。

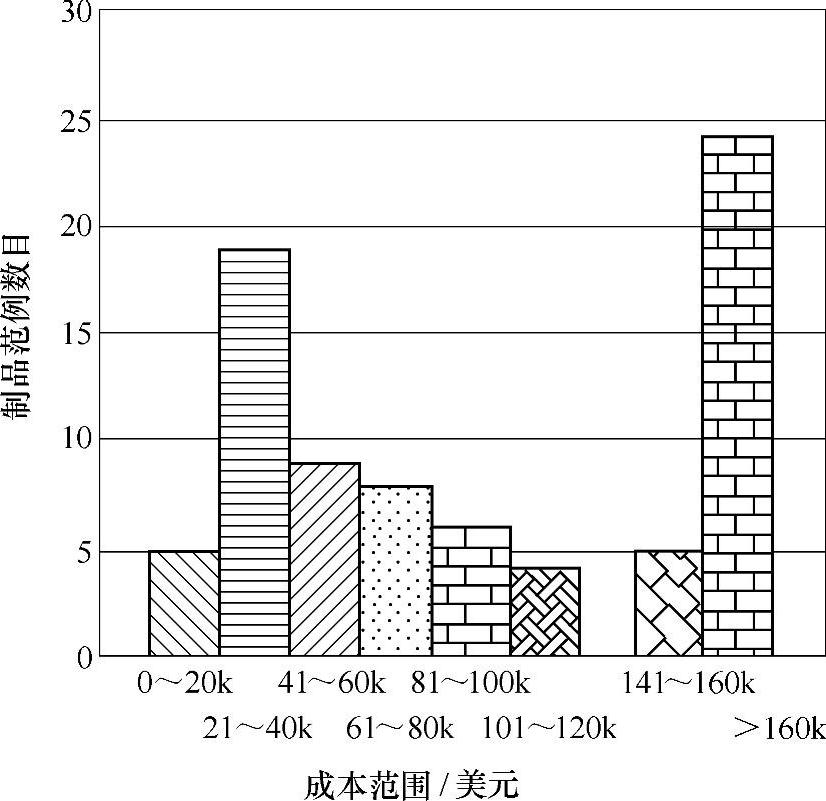
图6-11 制品范例成本分布

虽然收集的制品样本，仅是公司生产模具的一部分，但已充分代表整个范围里模具的大多数。例如：注射制品样本的质量从2g到2000g，投影面积从5cm²到14360cm²，其成本为20000美元到500000美元，见图6-11所示的制品范例成本分布。

3.系统网络线路

系统网络的操作有三个阶段。要从一些输入到输出范例中，搞清输入与输出关系。第一步选择系统网络结构，包括层的数目，每层的神经元数目和每层所用的转换功能。第二步用所选择的系统网络，操作所使用的范例，直到在实际输出和目标输出之间的误差趋于收敛。如果误差在已定目标误差之内，认为操作完成。第三步，用一些测试范例来测验操作的系统网络。测试的范例不是操作实例。如果概算的误差在测试范例的目标误差内，操作和测验认为是成功的，系统网络使用顺利。通常，整个过程是操作-误差的反复迭代。

（1）系统网络的构建 反馈传输系统网络应用MATLAB系统网络工具箱，完成程序编写。在输入层，一些神经元与成本相关因子是相同的，为上述CF₁～CF₁₉的应用。在输出层仅有一个神经元表述成本。系统网络有一个或者很多个隐藏层。实际上，近似的非线性关系有个隐藏层就足够了，所以，这里应用了一个隐藏层。隐藏层的转变函数是tan-sigmoid；而线性函数purloin用在输出层。此系统网络的结构说明在图6-12。在隐藏层中神经元的数目需要决定。CF是输入向量。W1是输入层和隐藏层之间内部连接的权重矩阵；W2是隐藏层和输出层之间内部连接的权重矩阵。B1和B2分别是在隐藏层和输出层里的神经元的偏置向量。

表6-23 92套CFs的设置和成本数据

（续）

（续）

（续）

图6-12 成本概算的BP逆向传输系统网络

（2）操作过程 以上陈述的系统网络，已经用逆向传输操作规则（back propagate training rule）进行了测试。隐藏层中的神经元数量需要决定，所以在各次的操作-误差循环期间，开始动用20个CFs神经元，每次操作有10至100个CFs神经元的增量。每个专门系统网络中，用随机功能以-1到+1之间赋值。然后将权重和误差，逐次调整到最小的网络误差的平方和。朝着误差急剧下降方向，不断改变权重和误差。

通常，操作运行在以下一个条件下即可停止。

1）误差的平方和，比用户目标误差小；

2）达到数量最大信号。

然而在目标误差未知时，可观察误差的平方和收敛于某个值的趋势，作为操作次数增加的信号。所以，设置的目标误差实际上不能达到。另一方面，在任何瞬时，都计算误差的平方和的相对变化率（relative changing rate）。每当500次操作完成时，给出如下相对变化率

i=1，2，3…

SSE_{（i+1）×500}=在（i+1）×500次的误差平方和；

SSE_i×500=在i×500次的误差平方和。

设置的最大测试次数是很大的数值，才能保证操作中，误差的平方和收敛于一定值。在测试500次后的每个校核点，如果0.99<RCR<1.01，则操作停止。

为了能更快地操作网络，用两种措施提高测试效率。动量和适应速率（momentum and adaptive learning rate）已经被联接到操作程序中。动量可以减少逆向传输中，对表层细微枝节的敏感性，帮助网络避免因微小误差而阻塞。另一方面，高的适应速率能保证网络畅通。然而，如果适应速率太大，研究问题时就会跳过微小的误差而不能收敛。适应速率的使用，能做到让运行步距大到足以保持运作速率。

当完成了系统网络的操作后，误差平方和依照的相对变化率RCR收敛。观察到大多数操作实例概算误差都达到很小的值，相对误差小于5%。然而，这并不意味着系统网络操作得很好，还会有数据失常（over-fitting）。过程的验证必须应用系统网络，校核是否具有概括能力。应用系统网络的实例来引导验证过程，并不包含在操作过程里。这些实例的概算成本与它们实际成本作比较，如果这些实例的相对概算误差，与操作实例是可比较的，系统网络被认为是有概括能力的；否则，这是个失常网络，不能使用。

（3）操作和验证结果　在目前的应用中，在表6-23中的92个CFs范例，都用来作为操作的实例。在表6-24中另外的10个CFs作为验证范例。共有9个系统网络被操作，神经元的数目在隐藏层中从20到100的范围内。经几次测试后，在RCR标准下它们作为收敛处理。然后应用10个验证范例，对每个范例的相对概算误差（relative esti-mation error，REE）计算式：

这里Cost_i，e是概算成本，Cost_i，a是范例i的实际成本。操作9个不同的系统网络，对于10个范例的REE结果，表述在表6-25中。最后一列说明了10个范例的REE平均值。

系统网络在隐藏层中70个神经元能得到最好的结果。而其他的结果则很差。NN_0→∞的系统网络覆盖了模具中整个范围的成本。在10个CFs范例中，REE的平均值是4.6%，范例7有最大的REE值为14%。对于早期注射模成本概算，这个结果很让人满意。

（4）不同成本范围的系统网络 当范例的成本范围很大时，操作中很难找到系统网络能容纳范例的最大和最小两头的成本。这涉及要有最好系统网络的构造和参量的问题。举例说，在表6-25中除了隐藏层的70个神经元外，其他验证范例生成概算误差很大。解决这个问题的途径，是对系统网络建立不同成本范围。在目前的研究中，已注意到图6-11中，有43个范例的成本小于6万美元；另外49个范例的成本大于6万美元。因此，决定建立起两个系统网络来处理这两组范例。这两个系统网络通过测验来决定隐藏层的神经元数目。它们的结构是相同的。表6-26中的验证范例被用来测试各自的操作网络。

表6-24 验证范例数据

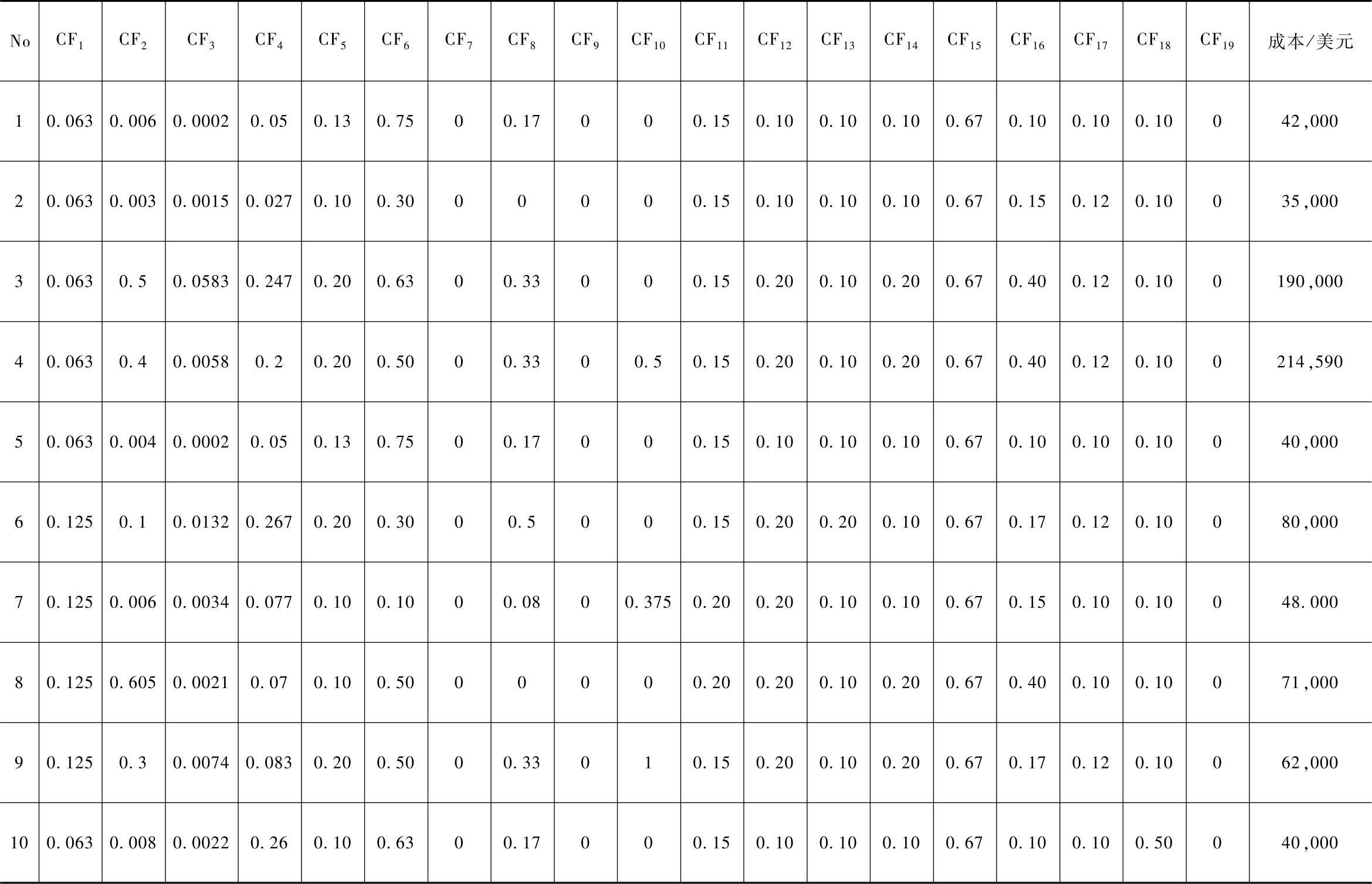
表6-25 验证范例的相对概算误差

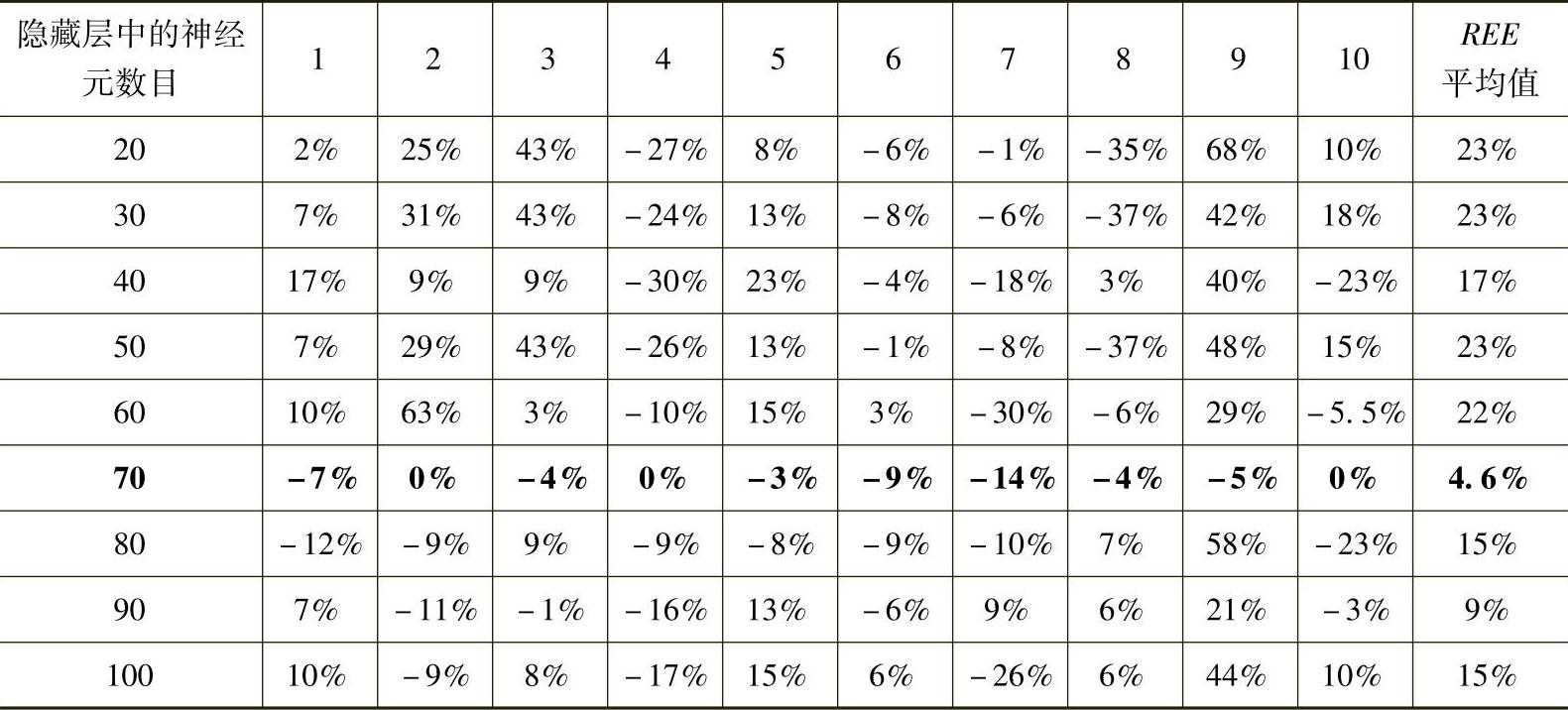
表6-26 验证范例的相对概算误差（<6美元）

因为43个范例成本小于6万美元，所以测验9个系统网络。在表6-26中10个范例中的6个（编号1，2，5，7，9，10）成本小于6万美元，所以测试它们。测试9个不同的系统网络的6个范例，其REE结果在表6-26中列出。其中的最后一列显示了6个范例的REE的平均值。隐藏层的70个神经元产生了最好的结果，REE的平均值为3.1%。其他的系统网络也产生了很好的结果。70个隐藏的神经元表达为NN₀→60k。

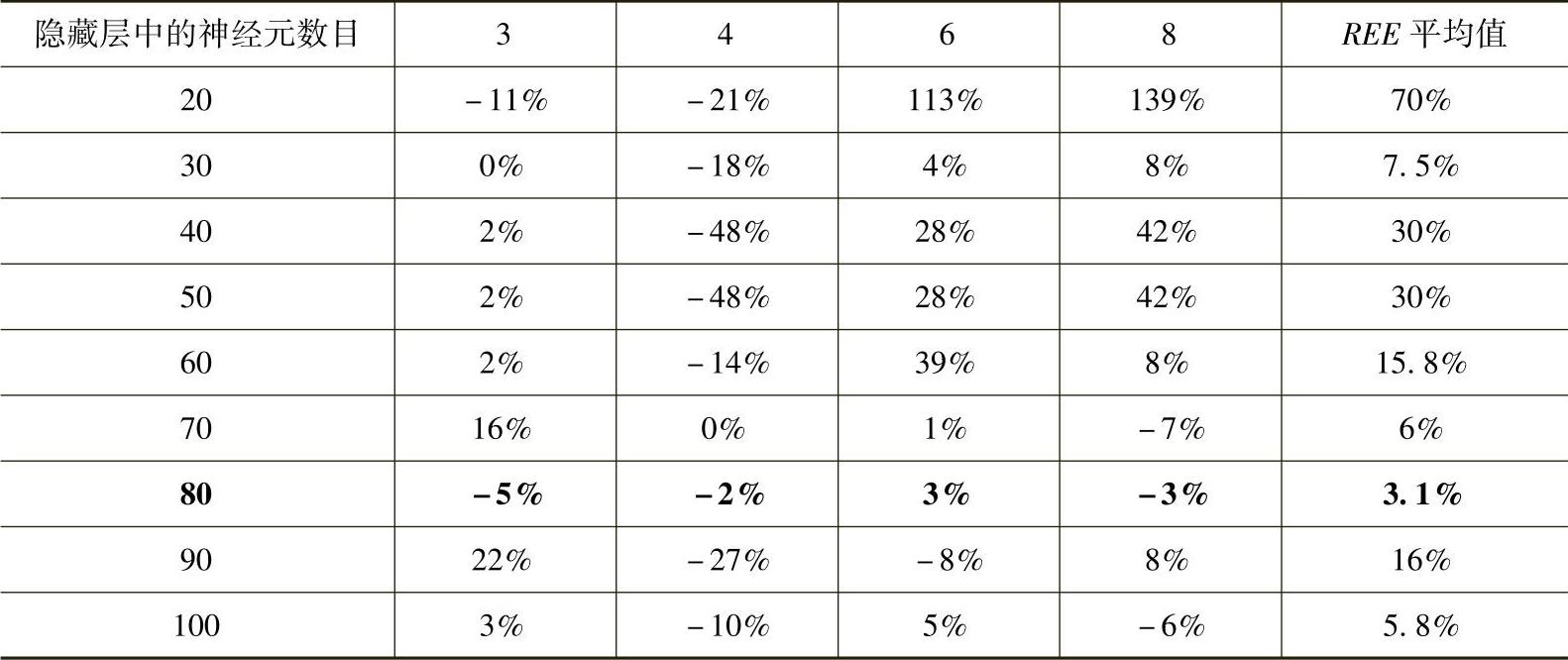
因为49范例成本大于6万美元，所以9个系统网络同样要经过测验。在表6-24中10个范例中的4个（编号3，4，6，8）成本大于6万美元，所以它们也用来测试。测试9个不同的系统网络的4个范例，其REE结果示列在表6-27中。其中的最后一列显示了4个范例的REE的平均值。在隐藏层中的80个神经元产生了最好的结果，REE的平均值为3.1%，这个系统网络表达为NN_60k→∞。另一方面，测试其他两个系统网络，在隐藏层中有30到100个神经元，同样也产生较令人满意的结果。也使得在不同成本范围下，增强了对各不同系统网络的操作功能。在这种方法下，对某个成本范围很容易寻找并操作适合的系统网络。

表6-27 验证范例的相对概算误差（>6万美元）

在目前的三个测验系统网络中（NN_0→∞，NN_0→60k，NN_60k→∞），必需有为注射新制品成本概算的策略。这里成本概算过程分为三个阶段。

1）给出新注射制品和成本提取和量化相关因素CFs。

2）应用NN_0→∞概算模具的成本Cost_rough。

3）如果Cost_rough<6万美元，应用NN₀→60k生成模具的最终概算成本；其他情况，可应用NN_60k→∞最终生成模具的概算成本。

4.综述

传统的模具成本评估存在一些问题。因为在早期的成本概算时，无法利用成本函数形式，也不能利用实用的历史成本数据直接校正成本概算。应用系统网络的成本函数近似处理方法目前已表明有助于解决这两个问题。这种处理方法能应用于注塑模的成本概算。在注射制品设计和模具概念设计时，在早期的估价阶段，都要定义注射模的成本相关因子CFs，在发展中安装有效的信息。对所有这些CFs在可能状态下的量化方案已经建立。从先期生产的一些模具，注射制品范例的CFs提取和量化，使其与它们的实际成本一致，已经发展了系统网络的程序结构，决定了构造、操作和验证。验证结果证实，此方法能够满意地概算成本。对不同的成本范围，操作使用不同的系统网络，能得到更好的结果。

总之，这种早期成本概算方法的优点如下。

1）成本相关因子CFs概括了模具概念设计和零部件设计中所有方面的成本。行情工程师和模具设计者能容易提取这些因素。

2）没有必要知道成本函数的实际形式。利用先前生产模具的零部件设计和它们的成本数据，逆向传输系统网络通过近似函数引导它们的关系。

3）以系统网络的操作形式，建立的成本函数能被修改。用新的范例一次又一次调整自身来适应新的制造环境，再重新测试系统网络。

另一方面，这种方法也受到某些限制。首先，隐藏层的数目和每个隐藏层的神经元有操作误差。它会浪费时间，且不能保证最后的选择结构是最好的。第二，成本方面的CFs研读困难。此外，流行的系统网络模式不能提供设计者更好解决问题的工具。