注塑件是按照壁厚相等的薄板组合形体的结构设计的。由于聚合物熔体的高黏度和非牛顿性、不良的热传导性能,要求注塑件有较小壁厚,常见在5mm以下,而且整个制件的壁厚均匀一致,以使聚合物熔体有较稳定的流动充模过程,注塑件又有较均衡的冷却固化过程。热塑性聚合物熔体具有剪切变稀的特征,应使注塑件型腔在熔体充模流动时的剪切速率的大小和方向有合理分布,应使熔体保压补缩充分、注塑件密度均匀。
1.一维流动充模数值分析
一维流动模拟是对图2-24所示的两种典型的型腔,进行充模流动数值分析。图2-24a是中心浇口的圆盘形模具型腔;图2-24b为浇口在一端的长条形型腔。一维流动还应包括圆管流道内的流动。
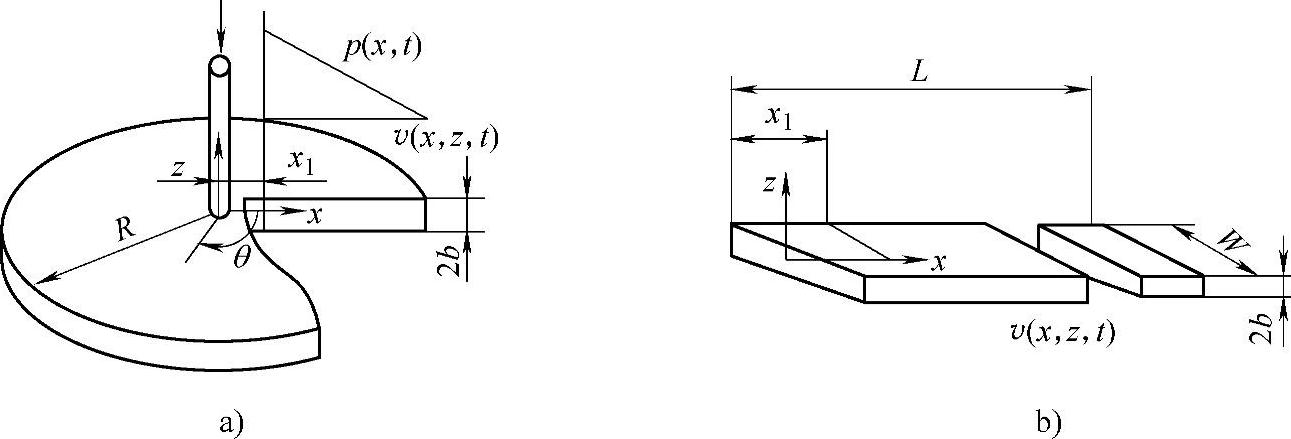
图2-24 一维流动的两种典型的型腔
a)中心浇口的圆盘形型腔 b)浇口在一端的长条形型腔
(1)控制方程及边界条件 由表2-2奈维-斯托克斯方程,直角坐标系(x,y,z)的x分量展开式,将牛顿黏度μ置换成非牛顿黏度η,有一维充模流动的动量控制方程

由式(2-1)黏性运动流体在非恒温条件下能量方程的直角坐标系的一维展开式
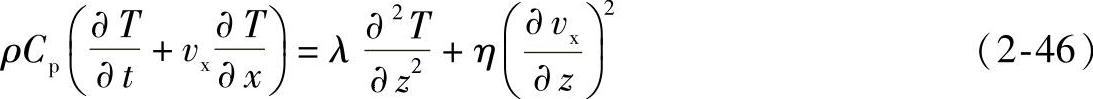
又有体积流率

式中,Γ(x)是模具型腔的形状系数:对圆盘形型腔,Γ(x)=2πx;对长板条形型腔,Γ(x)=W,W为长板条宽。
引入下列速度场和温度场的边界条件
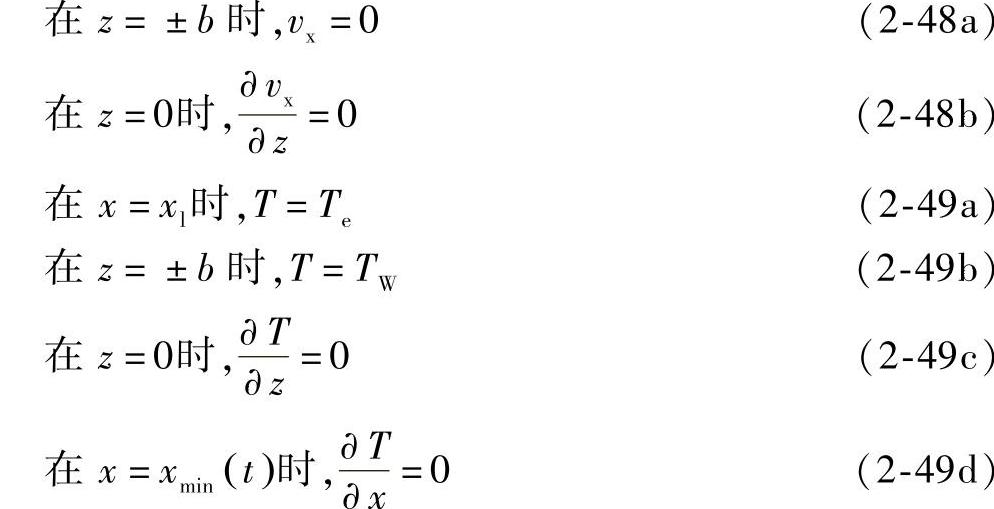
式中 Te——浇口处温度;
TW——模具型腔壁面的温度;
xmin(t)——t时刻熔体前沿的位置。
(2)一维压力场和温度场的数值解法 对式(2-45)积分,并将流量方程式(2-47)和边界条件式(2-48)代入,可得压力梯度

式中 p′——压力梯度的模,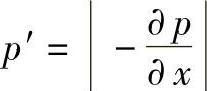
S——熔体的流动率。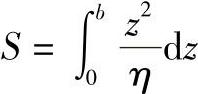
同时,还可求得剪切速率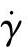 、流动速度vx和黏性热ϕ,有
、流动速度vx和黏性热ϕ,有

至此,可分析求解得出熔体流动时的压力场和速度场。
对于薄壁制件,可用有限差分法求解温度。由于温度场对称分布,可以考虑上半部分将图形分为若干等分,如图2-25所示。
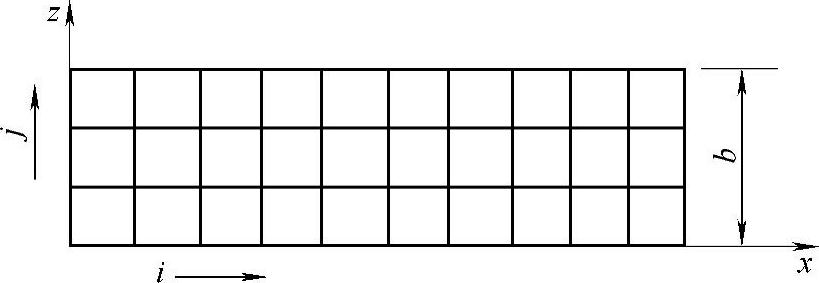
图2-25 有限差分法网格划分
温度场可离散为
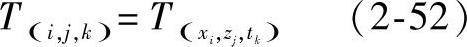
和表示网格位置有下列关系:
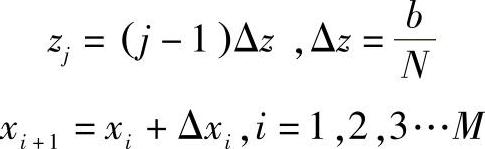
t1=0,tk+1=tk+Δtk(k≥1)
依照式(2-46)注射的能量方程,利用向后的差分格式,流动熔体能量方程的全隐式差分法分析式为
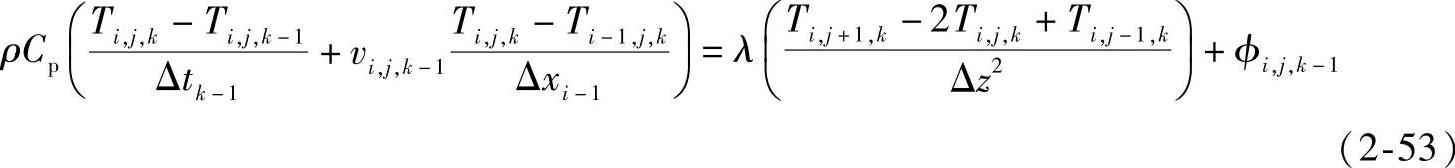
式中,速度场的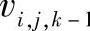 和黏性热
和黏性热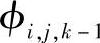 利用上一时刻的值。
利用上一时刻的值。
2.二维流动充模数值分析
注塑件在计算机造型后,进行有限元网格自动划分(常有三角形和四边形两种单元供选用),输入注射充模的温度、压力、时间和速度等工艺条件,选调注射机的技术参数,调用聚合物熔体材料的流变性能。一般流动分析软件有密度分布、剪切速率分布、充模熔体前沿流线、熔体温度场和压力场、熔合缝和气囊分布等。对输出结果有碍成型制品的质量,则需修改注塑件结构,例如壁厚等;也可修改浇注系统,例如浇口数目和位置等;也可修正工艺条件,直到实现合理的充模流动。
(1)流动分析的偶合路径法 建立起上述的一维流动数学模型,圆管、圆盘和矩形条的型腔基本流动单元后,还可以增添锥形管道等流动单元。为分析注塑件型腔中的流动,还需增添中心侧浇口的扇形流动单元,和中心侧浇口的圆环形流动单元,如图2-26所示。后者需要借助二维流动分析程序来模拟熔体在型腔内流动。
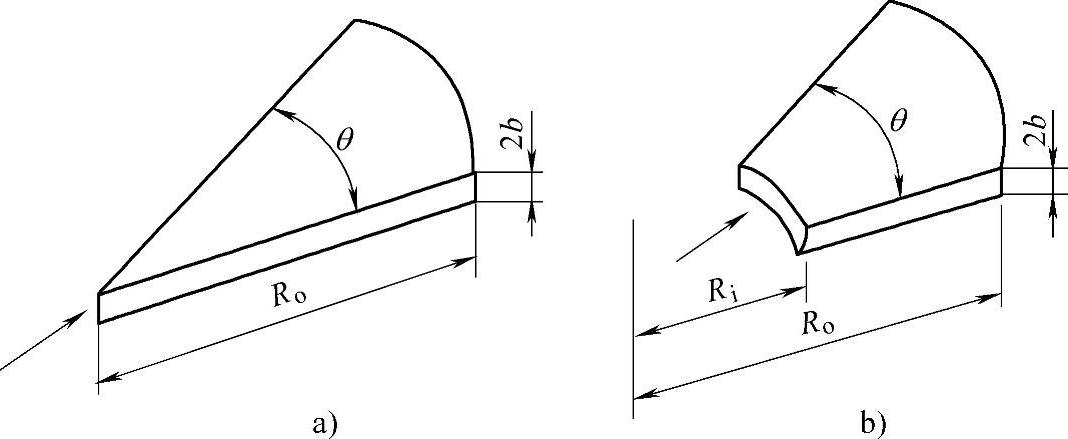
图2-26 二维的流动单元
a)中心侧浇口的扇形流动单元 b)中心侧浇口的圆环形流动单元
图2-27所示的注塑件,可采用二维的控制方程来分析熔体的流动。如图2-27b所示,将三维空间上的注塑件展平,再设置浇口,划分流动路径和流动单元。然后用一维和二维分析程序进行流动分析。这种划分流动途径,然后再根据各路径将型腔分解成若干串联的二维流动单元,称为耦合流动路径法(couple flow path)。
图2-27b所示的耦合流动路径,经计算机对注塑件造型后,由软件自动执行完成。其后的流动分析的步骤如下:
1)定义时间步长Δt=tf/(N·M),tf为充模时间,N和M是给定的时间间隔数。某一时间步长是对的路径上串联着的一个单元的流动,步长可根据单元的充满时间调整。
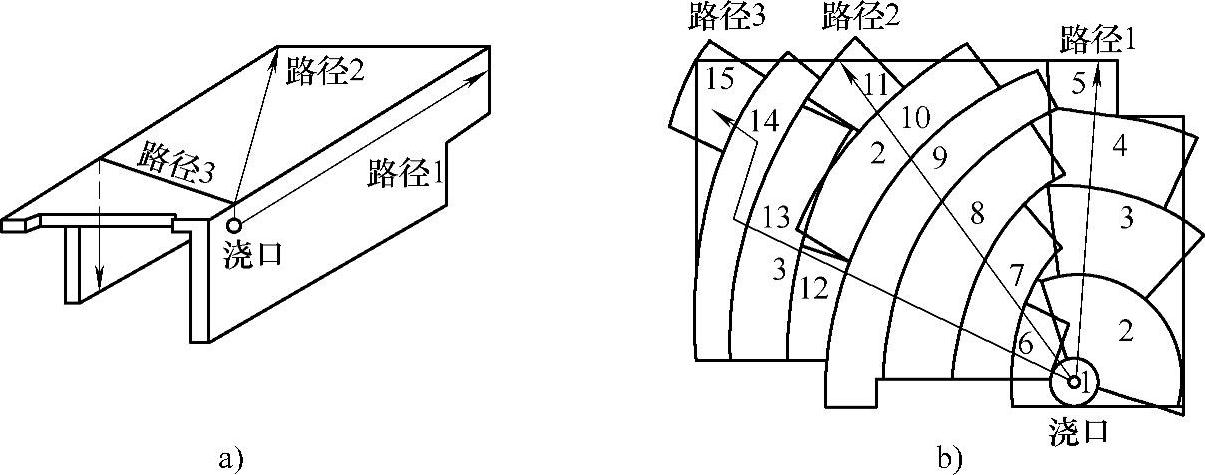
图2-27 注塑件的展平及划分器和流动单元
a)注塑件 b)展平及划分路径和流动单元
2)在某单元内的熔体流动过程中,在每个时间步长内都应更新该单元的温度场。
3)每条流动路径的入口压力近似相等。从浇口处的压力始,每条路径末端压力为大气压力。所以在任何时刻,每条路径的总压力降应该相等。根据这一条件,利用迭代法在每一时间步长内,沿每条流动路径更新各自体积流量。直到某流动路径的最后一个单元被全部充满。在后续的时间步长内,其体积流量为零。
4)根据更新后的体积流量,计算熔体在每一个未充满单元内的前沿位置。
5)计算单元内的压力场和速度场等。
6)返回步骤2,重复计算过程,直至全部流动路径内的单元均被熔体充满为止。
在一维和二维流动分析时,多用有限差分和有限元混合的方法。此种流动模拟能胜任模具型腔复杂的几何边界的处理。
(2)二维流动的控制方程 聚合物熔体在图2-28所示任意形状的扁薄的型腔间隙中充模流动。Ce表示浇口区;Co为型腔的边界;Cm(t)为t时刻熔体前锋推进位置。型腔间隙为2b,也即注塑件壁厚。坐标原点位于型腔间隙的中央面上,置于料流的起始位置。
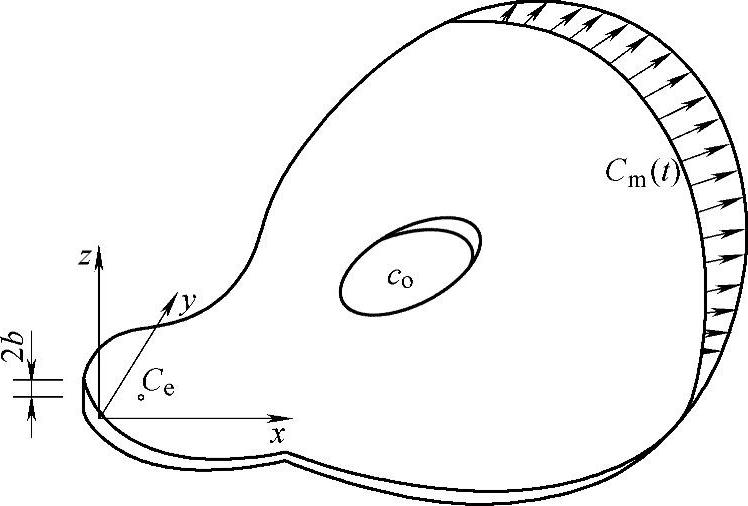
图2-28 聚合物熔体注射充模流动
1)二维的流动模型。考虑图2-28所示的薄壁二维型腔的充模流动,由前连续性方程、动量方程和能量方程的直角坐标系的展开式,有四个注射控制方程:
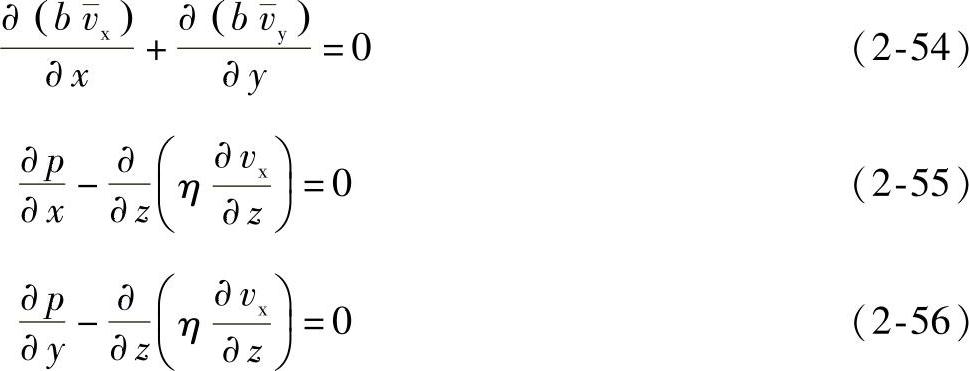
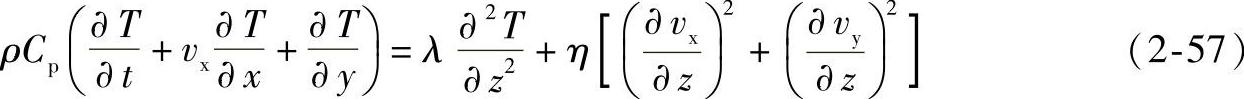
边界条件
z=±b,vx=vy=0,T=TW (2-58)(https://www.xing528.com)

在Ce浇口处
T=Te (2-60)
其黏度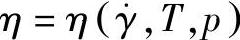
剪切速率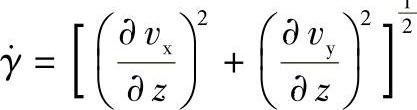
2)求解速度场。对式(2-55)和式(2-56)进行积分处理,并应用边界条件式(2-59),有
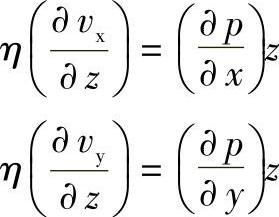
将此两式再次积分,并应用边界条件式(2-58),有

用式(2-61a)和式(2-61b)沿z方向积分,得熔体的平均流速为

这里熔体流率

3)求解压力场。将式(2-62)的平均速度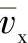 和
和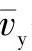 代入式(2-54),得压力场的控制方程
代入式(2-54),得压力场的控制方程

应用有限元法进行数值分析,要将式(2-64)偏微分方程演变成代数方程。应用伽辽金(Galerkin)加权余量法,引入权函数W。W为单元形函数。又运用散度定理,设Ω为型腔中熔体已充填区域。又将边界条件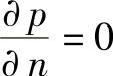 代入,n为型腔壁面的法向,可得到
代入,n为型腔壁面的法向,可得到
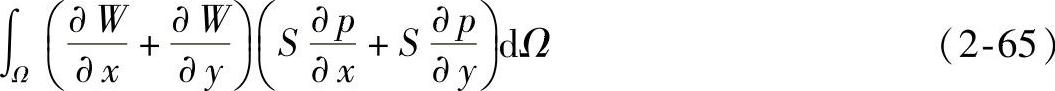
将区域Ω分成单元,单元内的压力分布用有限元法的多项式近似表达
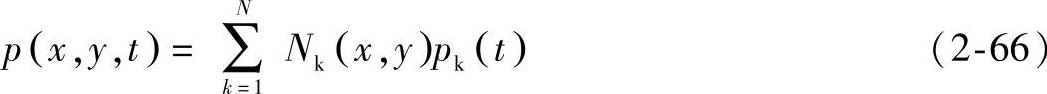
式中 N——单元的节点数;
pk(t)——单元节点t时间压力;
Nk(x,y)——单元形函数,Nk=Wk。
又有Nk=(ak,bk,ck)/2A
式中A为三角形单元的面积,其k=1,2,3。
有限元网格上各节点的压力,Nk用权函数依次求出。其权函数的常数ak、bk和ck要建立方程解出。有关有限元数值分析的进一步演示,请参阅有关专著。还有温度场的求解方程,熔体流动前沿位置和两股熔体前锋相遇等求解方程,这里不再列出。图2-29是一模有大小两件注射型腔的模拟分析结果。从有限元网格单元建立,到流动速度、压力场和温度场的分布显示。
3.保压过程数值分析
在保压阶段温度变化显著,压力变化幅度大,熔体密度变化大,必须考虑熔体的可压缩性,也因此必须采用更宽温度范围的黏度模型;同时,必须考虑熔体的比热容和热导率随温度的变化;在保压过程中存在固液相变化,必须考虑结晶型聚合物在熔点附近密度的突变及结晶潜热的释放。
(1)型腔内保压过程流变方程 型腔可简化为相距很近的两平行壁面之间的空间,如图2-28所示。又由表2-4,有连续性方程的直角坐标系(x,y,z)展开式
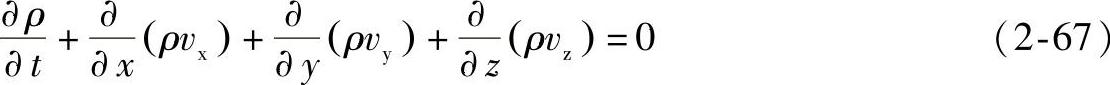
又有表2-2奈维-斯托克斯方程的展开式,直角坐标系(x,y,z)的x和y分量引进两个控制方程;又利用注射流动时的剪切应力和剪切速率的关系式,有
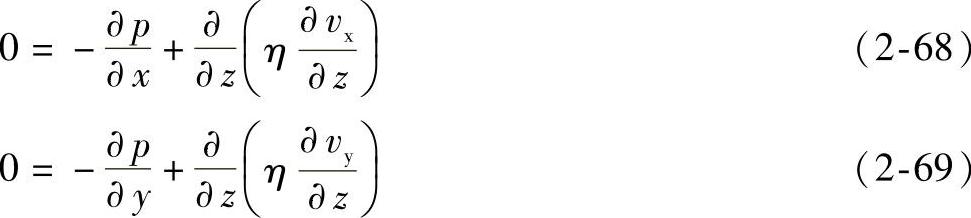
用能量方程式(2-57)
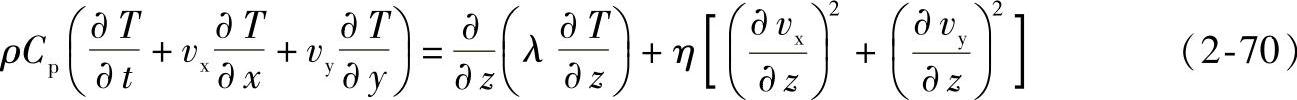
式中比定压热容Cp和热导率λ应为温度的函数Cp(T)和λ(T)。
(2)保压过程的控制方程 以上的二维的流变方程应推演成保压过程的控制方程。将密度随时间的变化,转化为密度随温度、压力的变化,随后再改写成计算机有限元数值分析的方程。
假设熔体的流动对型腔中心层对称,对于图2-28上的模壁处熔体无滑移,压力下的剪切流动的边界条件有
对于z=±b
对于z=0
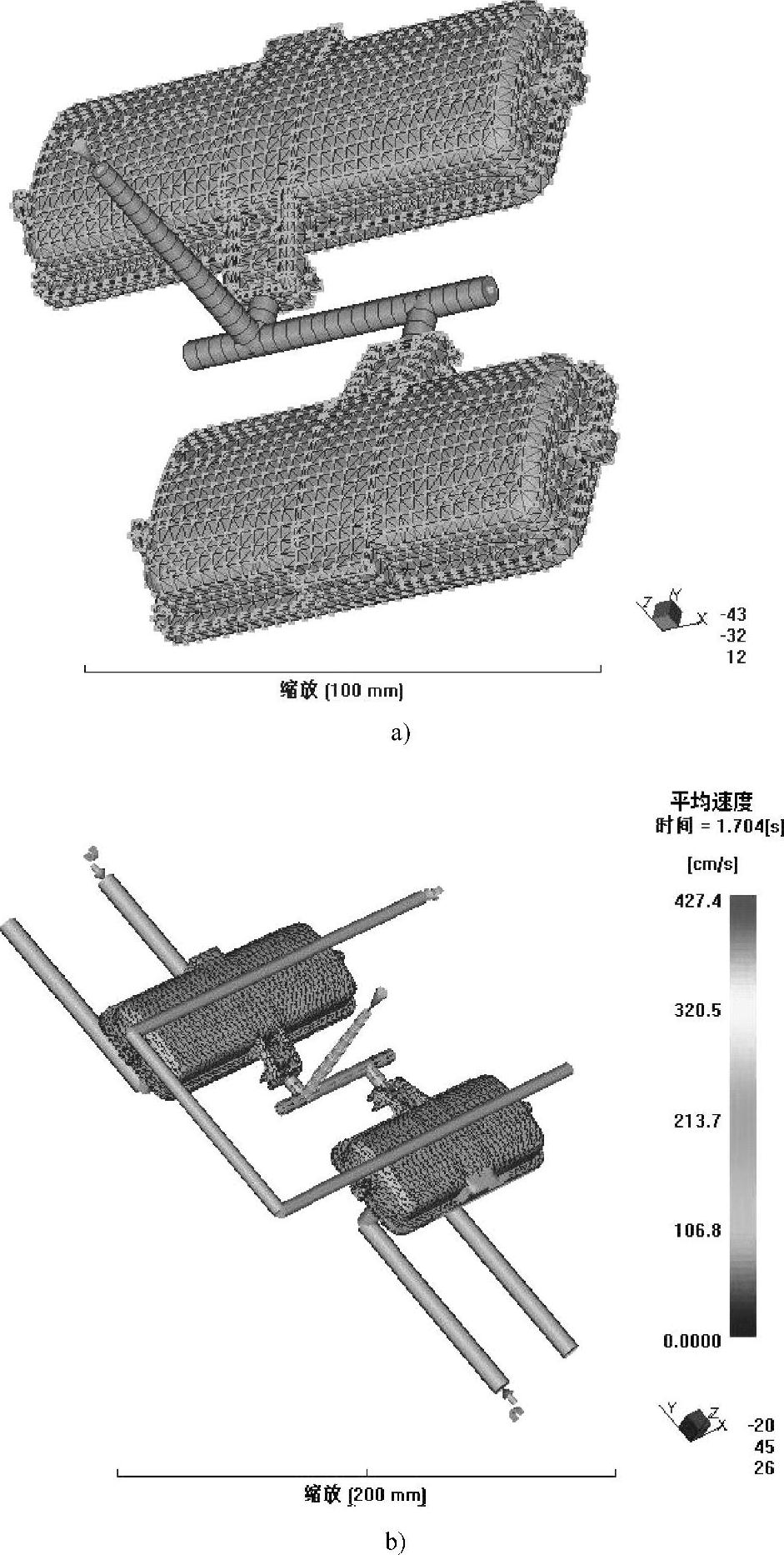
图2-29 计算机的熔体注射流动分析的演示
a)有限元网格单元 b)1.7s时流动速度分布
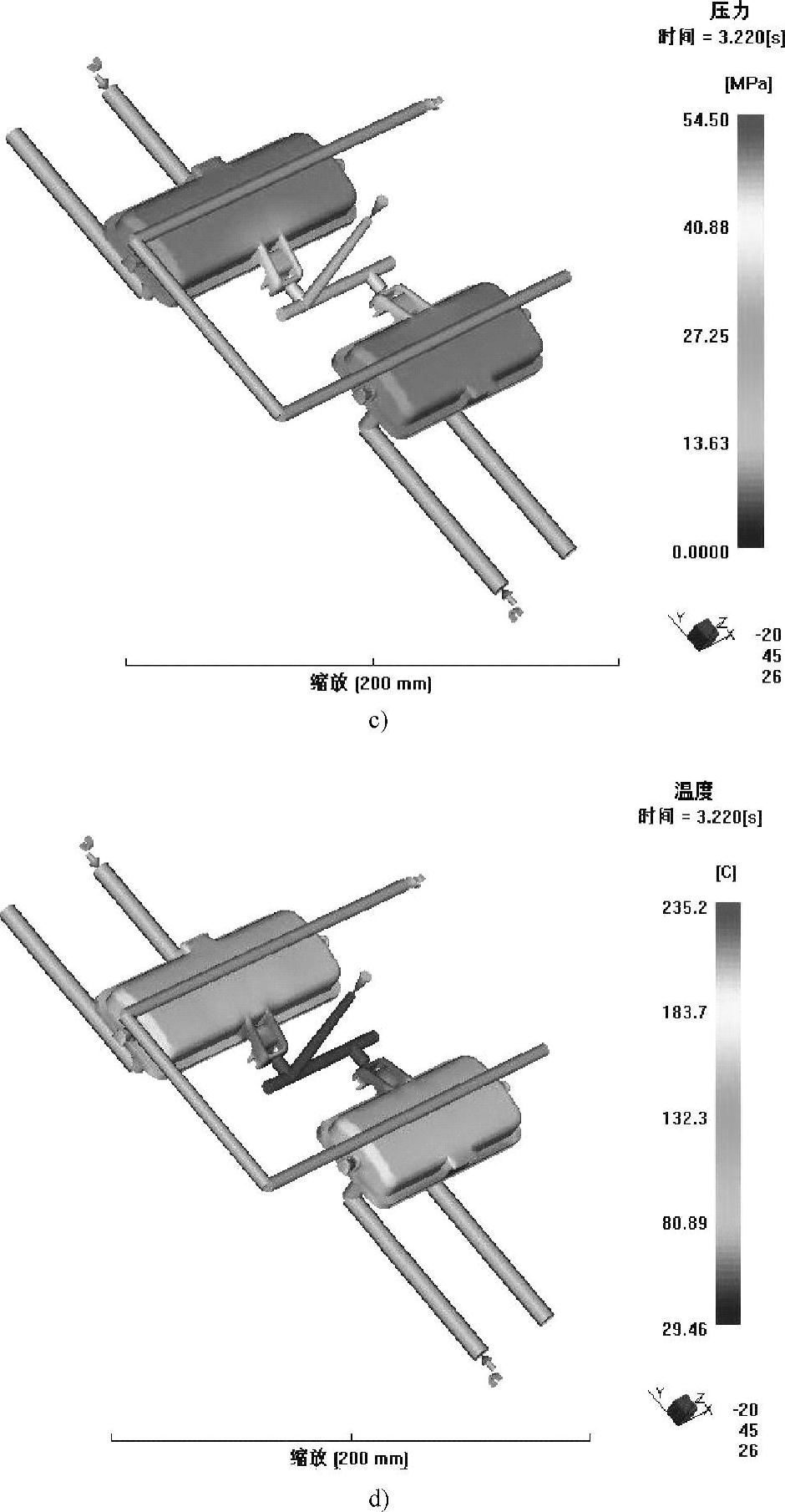
图2-29 计算机的熔体注射流动分析的演示(续)
c)3.2s时压力场分析 d)3.2s时温度场分析
分别对式(2-68)和式(2-69)在z方向积分,并利用边界条件式(2-71b),有

其中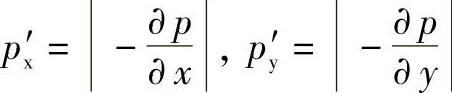
再次对式(2-72)积分,并利用边界条件式(2-71a),有

其中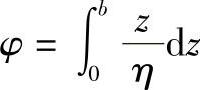
可得在方向上单位长度的质量流率为
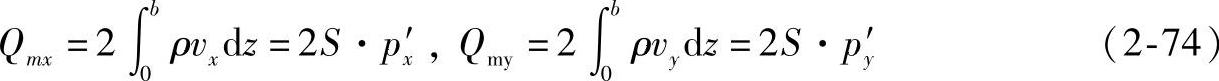
其中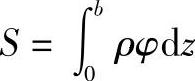
对式(2-67)在厚度方向上积分,则有
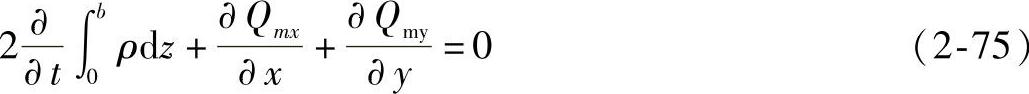
在保压阶段,密度ρ是温度T和压力p的函数。将式(2-75)中第一项密度随时间的变化,转化为密度随温度、压力的变化及温度、压力随时间的变化,有
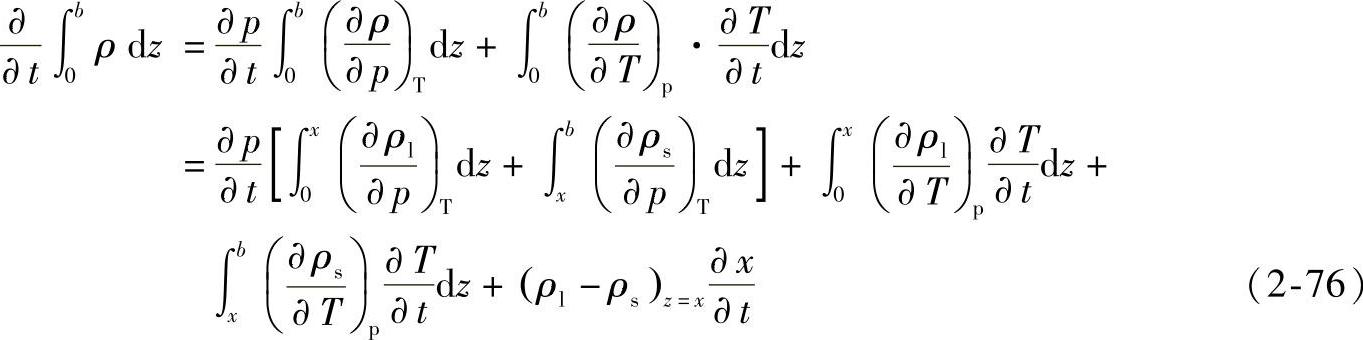
式中,压力在厚度上不发生变化,故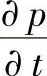 与z无关而可提到积分号前。其中下标l和s分别表示液相和固相;x是固液相交界面的位置;最后一项是针对结晶型聚合物在固液相交界面处,密度不连续而引入的。将式(2-76)和式(2-74)代入式(2-75),有
与z无关而可提到积分号前。其中下标l和s分别表示液相和固相;x是固液相交界面的位置;最后一项是针对结晶型聚合物在固液相交界面处,密度不连续而引入的。将式(2-76)和式(2-74)代入式(2-75),有

在保压过程中主要考虑压力影响。在迅速升高的压力下,制品密度大而使补料得以进行。G项起驱动作用使制品密度变化。在进入冷却阶段后温度变化大时,F项起驱动作用,使制品密度变化。直至浇口冻结,制品质量确定不变。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




