优化聚合物熔体黏度方程表达式及其参数

聚合物熔体在注射成型中的流动黏度η与压力p、温度T和剪切速率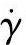相关。其熔体流动材料的剪切应力本构关系描述成

在注射流动过程的数值分析时，各种塑料的流动黏度的方程必须是压力p、温度T和剪切速率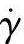的函数，其黏度η值随时供流动控制方程调用。

1.聚合物的普适流动曲线

大量的聚合物熔体的黏性流动实验和流变曲线，概括了图2-23所示的熔体的普适流动曲线。由于此类曲线的黏度与剪切速率的变化范围很广，所以用对数坐标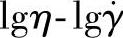表达。

1）聚合物的流动曲线可以分为三个区域：

①在低剪切速率下，斜率为零；在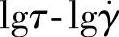坐标上斜率为1。此状态的流体符合牛顿流体定律，称为第一牛顿流动区。在lgη-lgγ·坐标的该区的黏度为零剪切黏度η₀，即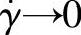时的黏度。

②剪切速率增大，流动曲线的斜率小于1，其流动指数n<1，称为假塑性流动区。该区的黏度为表观黏度η_a。在该区的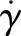增大时，η_a减小。聚合物熔体加工成型时所经历的剪切速率，通常在此范围内。

③当剪切速率继续增大，在高剪切速率区流动曲线为另一个斜率为零的直线，也符合牛顿流体定律，称为第二牛顿流动区。高剪切速率区的黏度为极限剪切黏度η_∞，即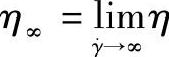。如图2-23所示，一般实验不容易达到这个区域。因为远未达到这个区域的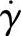值，已经出现了不稳定的流动。

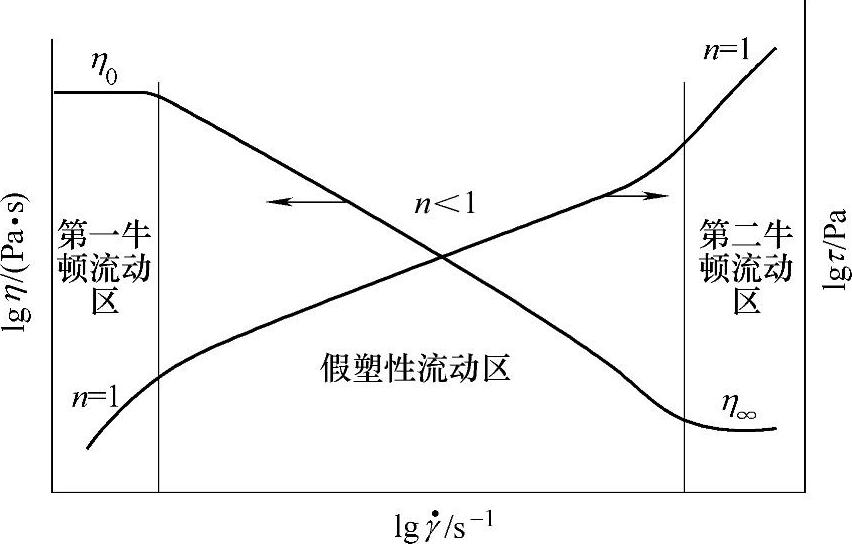
图2-23 聚合物熔体的普适流动曲线

常见的普适流动曲线是理论推断的示意曲线。聚合物的零剪切黏度、表观黏度和极限黏度有η₀>η_a>η_∞关系。

2）对聚合物的普适流动曲线的黏度特性，通常以分子链缠结的观点来解释：

①当聚合物的相对分子质量超过某临界值后，分子链间存在着相互缠绕点或因范德瓦尔斯力作用形成链间的物理交联点。在分子热运动作用下，这些物理交联点处于不断解体和重建的动平衡状态。整个聚合物熔体具有不断变化着的拟网状结构。

②在低剪切速率下，大分子链的高度缠结，流动阻力很大。由于剪切速率很小，链缠结点的破坏等于缠结的形成，黏度能保持恒定的最大值η₀，具有牛顿流体的流动行为。

③当剪切速率增大时，大分子链在剪切作用下发生构象变化。随着剪切速率增大，缠结的解除和破坏增多，而缠结的重建越来越少。大分子链和链段沿着流动方向的取向越来越明显。这样使流动阻力减小，表观黏度η_a下降，表现了假塑性的剪变稀的流动特征。

④当剪切速率继续增大时，在强剪切作用下，大分子链的拟网状结构完全被破坏。高分子链沿着剪切方向高度取向排列，流体黏度达到最小值η_∞，且有牛顿流体的流动行为。

2.聚合物材料的黏度方程

目前一些注射流动分析软件，采用的非牛顿流体的黏度方程有以下三个。(www.xing528.com)

1）取决于温度的幂律方程。它是基于阿伦尼乌斯（Ahrrenius）黏流活化能方程演变的经验公式。以

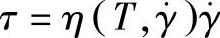
有

式中 n——流动指数，也称非牛顿指数；

T——聚合物熔体的温度；

A——聚合物材料的黏度常数；

T_a——与聚合物材料活化能有关的常数。

2）修正的五参数Cross黏度方程，它是五个材料参数（n，τ^∗，B，T_b，β）构成的。黏度是压力p、温度T和剪切速率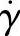的函数。

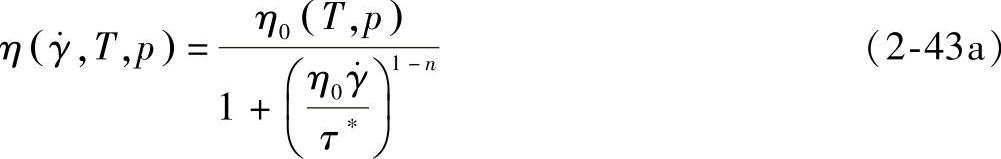
式中，n为流动指数；τ^∗为材料常数，描述了由牛顿黏度过渡到幂律黏度的剪切应力水平。零剪切黏度η₀是温度和压力的函数，采用阿伦尼乌斯类型方程表达式

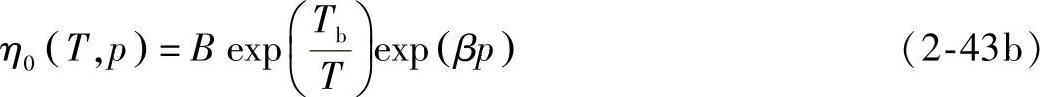
式中，B，T_b，β都是材料常教。B为材料的黏度常数；T_b反映η₀对温度的敏感性；β体现η₀对压力的灵敏度。

采用阿伦尼乌斯类型方程表达式（2-43b），不仅可以描述高剪切速率时熔体的非牛顿流体流动行为，也能描述低剪切速率下的零剪切黏度。在大部分聚合物熔体充填模腔时，能较为精确地描述黏度值，但不适用在保压阶段描述较低温度时的黏度。

3）修正的七参数Cross黏度方程，它是七个材料参数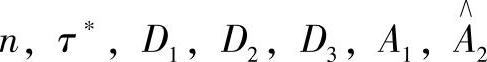（）构成的。黏度是压力p、温度T和剪切速率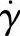的函数。零剪切黏度η₀（T，p）采用WLF（Wil-liams、Lardel and Ferry）类型方程表达式

其中T_s=D₂+D₂p

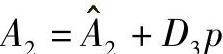
对于无定形聚合物，WLF类型方程表征的熔体黏度更接近于真实黏度。采用WLF型方程表达式（2-44），能在较宽的剪切速率范围内，描述聚合物熔体充填和保压过程的黏度。