多环带Q非球面视场拼接优化设计方法

采用微透镜阵列沿曲面排布的形式,存在信号串扰、抑制杂散光难度大、工艺难度大等问题。因此,本节进一步探索用环形拼接非球面替代曲面排布微透镜阵列的新型结构设计方法,即将同心球后表面及其附着的曲面微透镜阵列,用视场分割的Q非曲面替代的设计方法。

基于同轴构造的环带拼接面可以获得连续的光焦度变化,从而避免因光焦度突变给光学系统带来像差和杂散光。与12.5节阐述的环形拼接融合面型设计方法雷同,利用视场分割成像思想构造环带拼接面型的过程中,需要讨论同轴模型分视场环带面在连接点处的连续条件,使两环带在拼接区域矢高相等和连接位置斜率连续。在三维空间中,如图12-69(c)所示,L1为径向直线,L2、L3、L4均为非径向直线,若拼接面上任意一点均连续,需要使得表面上任意一条非径向直线均光滑连续。

位于YOZ平面内的径向直线L1内外环矢高分别用z1、z2表示,L1的连续条件为

取XOY平面任意一条经过环带连接处的直线,内外环矢高分别用z3、z4来表示。

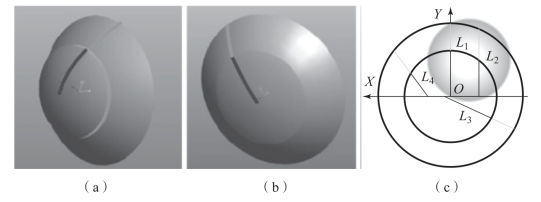
图12-69　相邻环带曲面的三维模型

(a)不连续;(b)矢高连续;(c)XOY平面

假设其直线方程为

其中,m、n为实数。

由几何关系可知

将式(12-66)与式(12-67)联立,可得

假设在环带连接处,h=h1,y=y0,则有

若对相邻环带均以二次曲面进行表征,由式(12-69)可得

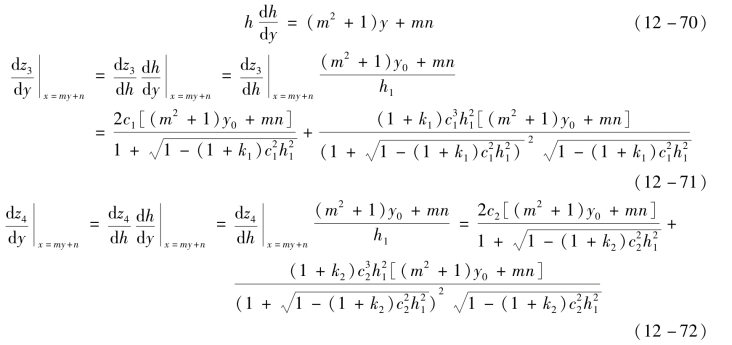
式中,c1、c2分别表示第内外环的顶点位置曲率;k1、k2分别表示内外环表面圆锥系数;h表示环带上点的径向距离。若令p=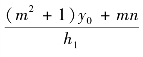,对比式(12-65)和式(12-72)可得

同理,

综上,若令环带拼接面在XOY平面上满足式(12-64)、式(12-65),则式(12-75)成立:

即在环带拼接非球面上,任意一条x与y线性相关的曲线都是光滑连续的。以上过程,证明了三维面型的环带拼接连续非球面,只要满足了径向连续条件,则在各个方向均顺滑连续,因此本节仅需在二维YOZ平面内讨论面型的连续性设计,即可获得三维空间的连续顺滑环带拼接面型。(www.xing528.com)

在环带拼接连续设计之前,需要首先得到各环带序列面的初始结构,各环带的初始结构设为球面,各分环带面的主要参数则包括每一环带焦距、后截距与球面曲率半径以及环带间的位置关系。各环带的分布则根据视场采取均匀分布,YOZ平面内等间隔的6个视场主光线位于各环带中心位置,分布在面型的不同高度上,如图12-70所示。

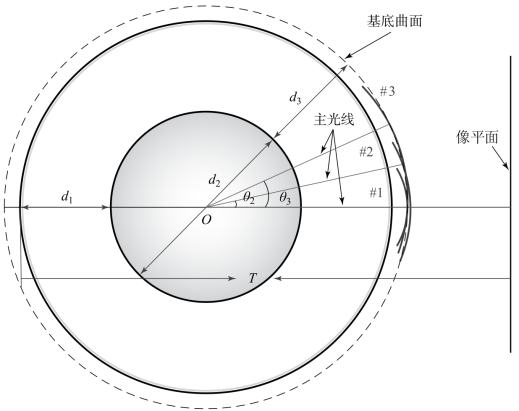
图12-70　系统结构及各环带(#1、#2、#3为例)位置分布示意图

图12-70中,全视场设计为±45°,6个采样视场以9°为间隔,越靠近边缘的环带曲率半径越大,从中心向边缘的环带分别记为#1、#2、#3、#4、#5、#6,各视场在光阑处主光线与系统光轴之间的夹角记为θi(i=1,2,…,6)。与曲面微透镜阵列面型设计时一样,环带拼接面基底半径设为1.123mm,则6个采样视场主光线与各环带面的交点均在基底曲面上,图12-70给出了中间三个环带对应主光线与环带的相交位置,内同心球后表面记为S3,环带拼接面记为S4,S3到S4中的材料与同心结构外球材料相同。

由光线追迹求解各环带初始结构曲率半径R4i的过程,如图12-71所示。近似地认为各视场主光线经过对应环带S4面时,主光线不发生偏折。已知系统总长为T,则各环带的顶点O与像点距离Li可由式(12-76)求得:

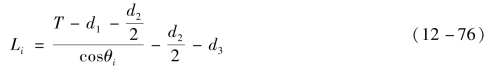
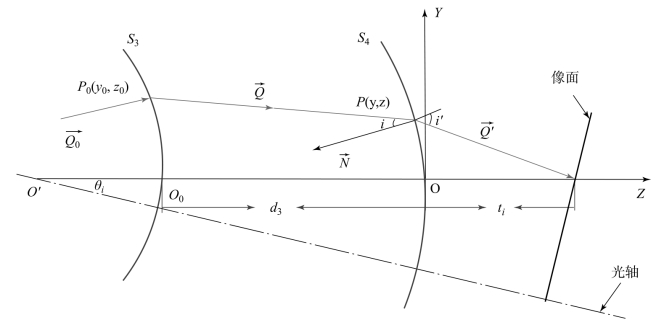
图12-71　各环带初始结构曲率半径R4i求解示意图

以第i个环带为例,以该环带顶点为原点建立坐标系,在二维YOZ平面内分析光路及系统参数,该环带对应视场主光线与系统光轴的夹角为θi。该视场边缘光线与S3的交点P0(y0,z0)经S3后,出射光线方向余弦为Q(mq,nq),P0点坐标及其对应的方向余弦Q参数y0,z0,mq,nq均为已知量。

则经P0点的出射光线所在的直线方程为

假设S4的曲率半径为R4i,且任意环带的曲率中心均在系统光轴上,则可求得位于系统光轴上的球心坐标O′(yOi,zOi)。该环带所在的曲面方程为

其中,球心O′的坐标参数yOi,zOi均为R4i的函数,联立式(12-77)和式(12-78),求得光线与S4的交点坐标P(yp,zp),其中yp,zp均为R4i的函数,可表示为P(yp(R4i),zp(R4i))。

已知该环带理想像点与原点O之间的距离ti,则近轴像点坐标为(0,ti),由此可得经P点的出射光线矢量Q′(-yp(R4i),ti-zp(R4i))。则在S4面的P点处,入射光线矢量为Q(mq,nq),出射光线矢量为Q′(-yp,ti-zp),该点处表面法向为N(-yOi,-zOi),这些参数中mq、nq、ti均为已知量,yp、zp、yOi、zOi均为环带曲率半径R4i的函数。

由矢量运算法则,可得P点处的入射角i和出射角i′;同样,二者均为曲率半径R4i的函数;同时光线在P点处发生的偏折应满足折射定律:

式中,n4为同心球外层的折射率,n5为空气折射率。求解此方程即可得到该环带的曲率半径R4i。

环带延长线与同心球球心之间的轴向距离记为τi,此时,光阑中心位置位于同心球球心,轴上视场(θ=0)环带中心与基底曲面相交,τ1=d3+,其他环带则满足

r1、r2始终为同心球结构外球和内球曲率半径。综合考虑结构的连续性和紧凑性的需求,结合内窥物镜的成像分辨率和设计视场范围,将各环带焦距范围定为1.2～2mm。选定系统长度T以及第三间隔长度d3,可以根据式(12-76)～式(12-80),获得环带基底的主要参数,如表12-26所示。图12-72为全局坐标系下的YOZ平面各环带面型轮廓及环带间矢高差。

表12-26　环带基底的主要参数

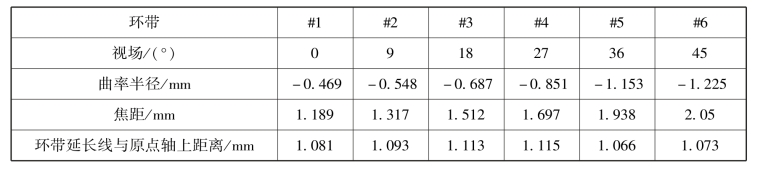
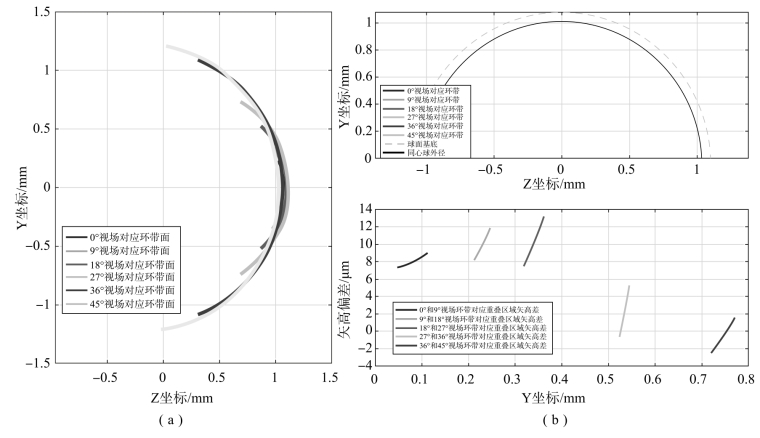
图12-72　全局坐标系下的YOZ平面各环带面型轮廓及环带间矢高差

(a)球面基底及6个环带面型的表面轮廓;(b)+Y向各环带局部轮廓与相邻环带面重叠区域矢高差