环形拼接Q非球面的定义及特征分析

分段拼接非球面的数学模型,一般是建立在各序列面为偶次非球面的数学描述方式上的。但如前文所述,采用传统的偶次非球面优化设计时存在诸多问题,尤其是面型控制能力有限,优化效率不高等。而在环形拼接非球面的设计中,各序列曲面的融合与优化控制方法是设计的关键,所以对拼接曲面连接点处的矢高与斜率问题尤为关注。针对这一问题,本书充分发挥斜率可控的Q非球面的优势,折反混合透镜的前后表面均采用环形拼接Q非球面表征。

环形拼接连续非球面的控制约束条件,不仅适用于偶次非球面定义的环带曲面,也适用于Qbfs多项式定义的非球面。Qbfs环形拼接非球面,是由一系列Qbfs多项式表征的子孔径曲面拼接融合生成。为了使面型连续且光滑,设计时需要对这些序列曲面加以优化约束条件,并在设计中与光学设计软件的控制符相结合。

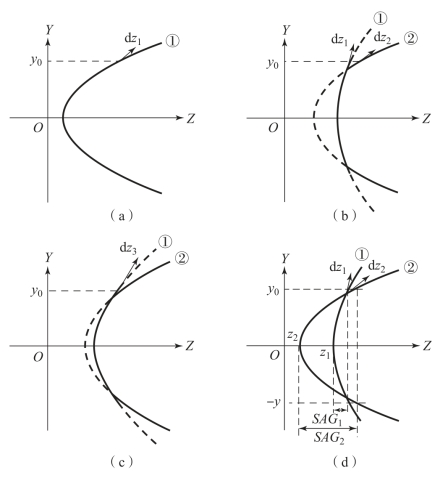
根据三维空间的面型约束条件可知,必须满足环形拼接非球面连续顺滑的面型要求。因此,系统的设计方法在二维平面YOZ上展开讨论。设计优化时,应首先使相邻曲面在缝合处的矢高相等,即可保证两个环带在YOZ平面内相交。在此基础上,再优化调整两相邻曲面之间的相对位置以及面型参数,使其在满足系统成像要求的同时,面型光滑连接。在ZEMAX光学设计软件中,并非将矢高或斜率相等设置为约束条件,而是将相邻两曲面的矢高差和斜率差分别定义为新的函数DIFF_sag和DIFF_gradient,将其差值与零的偏离程度作于评判的标准。以相邻两曲面为例,图12-49(a)中,编号为①的Qbfs非球面,y0值由边缘光线或各序列曲面的口径决定;图12-49(b)示意了由两个不同方程定义的编号分别为①和②的Qbfs非球面,以及缝合处各自的切线向量;图12-49(c)中的实线部分为约束条件下,优化后的连续顺滑面型以及其在缝合处的切线向量;图12-49(d)标注了约束条件所需的参量,两相邻曲面的矢高分别记为SAG1和SAG2,交点处的斜率分别记为DER1和DER2。

(www.xing528.com)

图12-49　拼接融合相邻两曲面约束条件示意图

(a)单个Qbfs非球面;(b)相邻两非球面;(c)环形拼接非球面;(d)相邻两曲面参数

在优化设计的过程中,拼接面的顺滑度与高像质往往相互制约,即矢高差和斜率差越大,成像质量越好;相反,随着两差值的减小,成像质量呈下降趋势。所以,要根据当前优化结果不断调整两个优化条件的权重,使两者平衡。由于相邻两曲面的表征函数不同,所以DIFF_sag和DIFF_gradient不可能为0,当两个函数值趋近于0时,则判定当前面型满足环形拼接连续非球面的面型要求。设立判断条件,即当矢高差小于镜面加工所要求的峰谷(Peak-to-Valley,PV)值误差时,则认为相邻两曲面的矢高是连续的。当使用数控机床加工环形拼接非球面时,可以同时加工多个小口径序列曲面。加工过程中,相邻两曲面的连接处不存在断点时,即认为相邻两曲面的斜率是连续的。因此,相邻两曲面的矢高差和斜率差与零的偏离程度,是否满足系统的面型要求,依赖于加工和检测的精度。现在的加工工艺已经可以加工出PV值小于10nm的光学表面,但是常用的面型检测方法或仪器很难达到这一精度,所以从某种程度上来讲,检测精度作为主要的评判标准。根据现有的检测水平,若矢高差值为10-5mm数量级,相当于PV值大约为0.1λ～0.2λ,认为矢高连续;若斜率差值为10-4数量级,认为斜率连续;并且,以上的标准是在设计阶段对环形拼接非球面面型连续且光滑的约束和判断,在实际加工过程中,随着不断地精磨和抛光,矢高差值和斜率差值将会进一步缩小。