消球差衍射光学元件的优化设计方案

前述章节中,已经介绍过利用赛德系数表征初级波像差的基本理论:

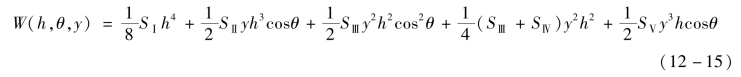
式中,y为归一化物高;h是光瞳上的规一化径向坐标;θ是光瞳中的方位角。SⅠ～SⅤ分别是球差、像差、像散、场曲和畸变的赛德系数。

如果L表示拉格朗日不变量,M表示共轭参数,X表示弯曲参数。在衍射曲面中弯曲系数被定义为

式中,焦距f与衍射面相位分布中的二次项系数及工作波长有关,m为衍射级次,cdiff为衍射元件基底面曲率。由此,可以得到以下衍射透镜的赛德系数方程:

式中,a2是轴对称衍射面相位分布中的四次项系数。该方程推导过程中,已根据衍射光学元件光线追迹常用的Sweatt模型,将衍射光学元件看作具有极高折射率的薄透镜,即取。

上述的赛德公式,给出了衍射透镜衍射结构基底面曲率对像差的贡献。可以将衍射结构理解为衍射透镜的附加效果。由此可以看出,衍射面相位分布系数a1和a2对赛德像差均有影响。a1决定了衍射光焦度,并通过上述公式中的弯曲参数X间接改变像差。可见,衍射结构基底面曲率对像差校正具有十分重要的作用。由于在曲面上制作衍射光学元件较为困难,通常情况下都采用平面作为基面。由赛德方程可以看出,孔径光阑位于衍射面时,系统场曲及畸变均为0。如果选取到合适的a2参数,球差也可以校正为0。这对于普通球面光学元件来说,是不可能实现的。

当成像物体位于无限远时,共轭系数M=-1。根据式(12-16)可知,当衍射面基面曲率cdiff=1/f时,弯曲系数X=2,此时若相位分布中的四次项系数a2=0,则SⅠ与SⅡ均为0,即球差和彗差同时为0。此时,衍射面基面曲率中心与像面重合,满足齐明条件。因此,这种情况下初级像差中仅剩像散,其余四项系数均为0。

当孔径光阑不再与衍射透镜重合,二者之间存在一定间隔,将引入视场像差。此时,引入比例平移α=Δhz/hz,其中hz为光阑密接衍射元件情况下近轴边缘主光线在衍射元件上的高度,Δhz表示光阑移动后,主光线在衍射元件上高度的变化量。像差系数将变化为

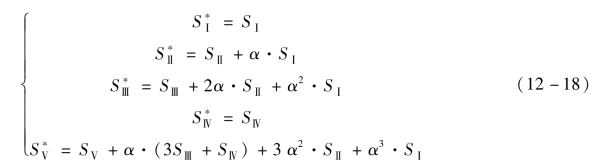
从上述两组像差系数方程组可以看出,孔径光阑位置变化前后场曲始终为0。由此可知,衍射透镜不论光焦度大小,在光学系统中对于场曲无任何贡献;另外,与普通透镜系统一样,只能通过移动孔径光阑抑制衍射透镜像散。

下面通过一组设计实例展示衍射光学元件校正球差的能力。设计要求采用单透镜完成焦距f′=20mm,f/2镜头设计。分别采用三种不同设计形式实现这样的设计指标。三种设计中衍射面均位于第二个面,透镜材料采用K9玻璃。其中,第一组设计的第一面、第二面均采用普通球面面形,衍射面仅含有二次项系数以校正色差。因此,衍射面径向空间频率与径向位置成线性变化关系(图12-11),并且由于等效阿贝数相对较小,整体局部光栅频率并不高。由横向及轴向像差曲线(图12-12)可见,单色像差校正很差,主要原因在于缺乏高次相位的补偿。

第二组设计中,第一面、第二面仍旧为球面,而衍射面相位分布中除包含二次项系数以外,还引入四次项系数,以对球差进行补偿。由图12-13可见,局部空间频率呈现非线性分布,并出现零值点。由图12-14可见,此时具有一定球差校正效果,但色球差较为显著。

第三组设计中,透镜第一面采用非球面,第二面仍旧采用球面,衍射面相位分布仅包含二次项系数,如图12-15所示,此时衍射面局部相位分布与第一组设计相同。由图12-16可见,像差校正取得了较好的效果。(www.xing528.com)

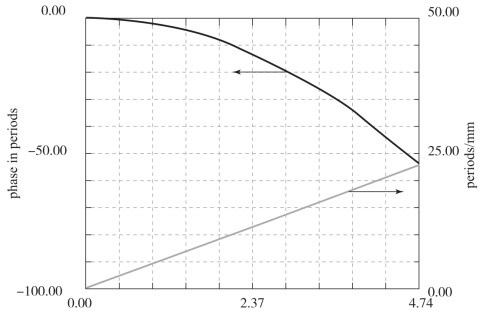
图12-11　第一组设计中衍射面相位分布与空间频率分布

图12-12　第一组设计后的横向、轴向像差曲线图

(a)横向像差曲线图;(b)轴向像差曲线图

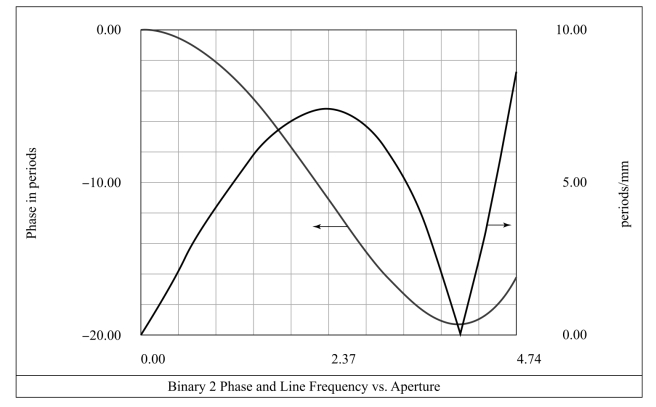
图12-13　第二组设计中衍射面相位分布与空间频率分布

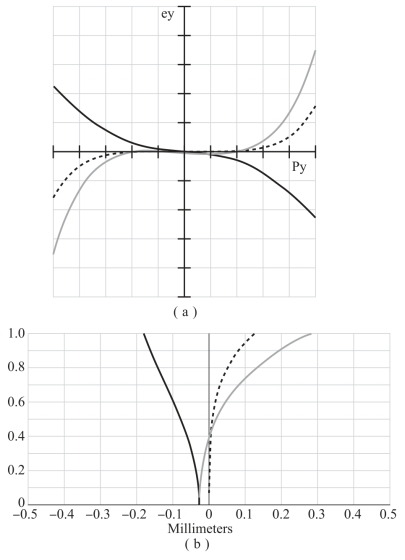
图12-14　第二组设计后的横向、轴向像差曲线图

(a)横向像差曲线图;(b)轴向像差曲线图

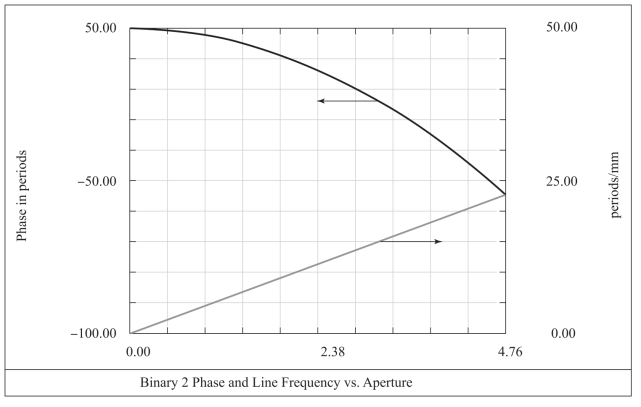
图12-15　第三组设计中衍射面相位分布与空间频率分布

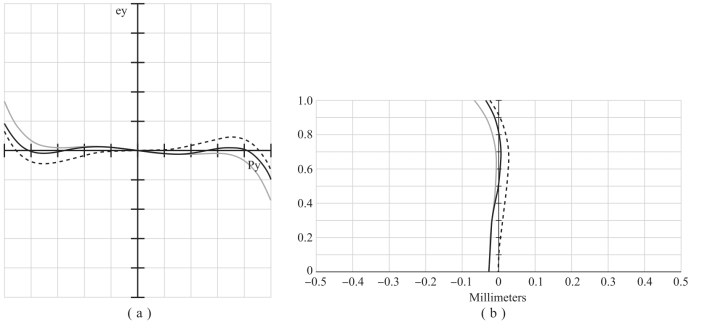
图12-16　第三组设计后的横向、轴向像差曲线图

(a)横向像差曲线图;(b)轴向像差曲线图