自由曲面反远心扫描镜优化设计

11.4.2.1　远心扫描镜的设计指标与单反射镜的成像畸变

离轴远心扫描系统通常也称为f-θ远心扫描系统,常应用于光学相干断层扫描、共聚焦激光扫描显微镜和多光子成像等。其像平面上弥散斑的大小在整个视场范围内受衍射极限的限制,基本保持恒定,从而在物方的扫描区域产生相同的成像分辨率。像方远心扫描光路可以最大限度地捕获来自物方的光束,且f-θ理想的映射关系是实现样品准确扫描的保证,无后期的图像处理。因此,会聚能力、像方远心度和f-θ映射关系是远心扫描系统的三大核心问题。

以Thorlabs Inc.出售的型号为CLS-SL的扫描透镜作为对照原型,并将设计结果与其对比,其主要参数见表11-9。CLS-SL透镜扫描系统可对方形视场成像,但是其入瞳必须位于两个振镜之间,通过双轴扫描的方式实现,图像质量会有所下降。所以,本章仅考虑单轴扫描,且离轴反射式的系统结构不引入色差,设计与之具有相同指标参数(有效焦距、入瞳直径和视场扫描范围)的离轴远心扫描系统,重点评价系统的会聚能力、像面畸变大小以及像方远心度三个指标。

表11-9　扫描系统参数和设计指标

由11.2.4节对多抛物面融合型自由曲面单反射镜成像系统的分析可知,畸变校正与远心度控制之间存在着相互制约的问题亟待解决。在±10.4°扫描范围内,f-θ畸变曲线如图11-28所示。0°～1.4°的视场范围,畸变值为负,其他视场畸变值均为正值。换句话说,在像平面上,满足f-θ映射关系的理想主光线大部分位于实际主光线之下。

11.4.2.2　自由曲面两反初始结构的生成

按照图11-17所示的自由曲面两反离轴远心系统的初始结构构建方案,将全视场分割为多个单视场单元,每个单视场单元由一对平面子镜和离轴抛物面子镜构成理想成像的子光路,由此形成由多个面对组成的两反成像系统。

离轴抛物面子镜实现光束的会聚和远心度的控制,平面子镜实现畸变的校正,从而达到无畸变远心成像的效果。融合各个离轴抛物面子镜形成自由曲面主镜,融合各个平面子镜形成自由曲面校正镜。按照表11-9中所示的设计指标,相应计算设置离轴角β0为50°。将自由曲面校正反射镜倾斜适当的角度,使从入瞳出射的0°视场的主光线与入射至像面的主光线平行。根据自由曲面主镜在±10.4°全视场范围内的f-θ成像关系计算得到,β+θ为60.4°,β-θ为39.6°,取70mm。这样,D0和反射焦距分别为53.379mm和610.682mm,RB为114.473mm。LCP为自由曲面补偿镜到自由曲面主镜的距离。为了使系统结构紧凑的同时避免遮拦,将其设定为32mm,LEC为入瞳到自由曲面子镜单元的距离,为37.682mm。

图11-28　多离轴抛物面融合型自由曲面单反系统f-θ畸变曲线

为了校正系统畸变,使分割的单视场单元光束成像于理想高度,构成自由曲面主镜的离轴抛物面子镜单元需进行重构,重构后其相应的离轴角更新为

经计算,和分别为60°和39.1°。由此,视场角和多离轴抛物面子镜单元的离轴角之间的对应关系获得了更新。比如,视场+θ对应的离轴角β+θ更新为,视场-θ对应的离轴角β-θ更新为。为了更新这些参数,在光路中通过将多平面子镜单元(除0°视场单元)倾斜一定的角度来实现,使得主光线发生偏折。任意视场角i对应的平面子镜倾斜角度可以根据图11-17中的几何关系获取:

分割单视场单元对应的平面子镜倾斜角度曲线如图11-29所示,接下来需要将这一系列不同倾斜角度的平面子镜拼接融合为连续顺滑的自由曲面校正反射镜。各单视场单元光束经自由曲面校正反射镜反射的光束走向由其坐标和法向量决定,需要对构成这些平面子镜的离散数据点进行拟合。但是,如果这些平面子镜的中心点均坐落在一个大平面上,那么,两两相邻的平面子镜在连接处的矢高,会因为各单视场单元对应的平面子镜的倾斜角度不同而偏差很大。因此,相邻的平面子镜在重叠区域的矢高差会对构造连续顺滑的自由曲面产成阻碍。那么,用于定位多平面子镜的基底的设计就显得十分重要,可以有效减小多平面子镜融合的难度。

多平面子镜基底的构建模型如图11-30所示,全视场±θ以相等的间隔Δθ进行采样。本设计中Δθ取0.1°,即全视场分为209个采样视场,对应的平面子镜的中心点记为P-104～P104,如图11-30(a)所示。这些平面子镜的中心点构成了所要求取的曲面基底,面型在局部坐标系(x,y,z)中定义。由于LEC远大于曲面基底的矢高,所以该基底在坐标系中y方向上近似于平面。假设Pk是视场kΔθ对应的平面子镜的中心点,则可以在三角形OP0Pk中根据三角定律求出点Pk的y坐标yk:

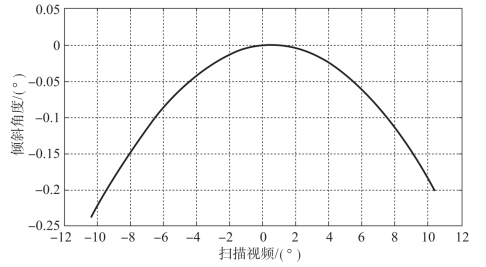
图11-29　平面子镜单元倾斜角度曲线

图11-30　平面子镜单元基底构建模型

(a)计算局部坐标y;(b)计算局部坐标z

z坐标可以根据P1,P2,P3,…,Pk-1逐点获取,如图11-30(b)所示。视场kΔθ对应的平面子镜的倾斜角用γk表示,相邻两个平面子镜的倾斜角的差值用δγk表示,表达式为

基底上相邻两个采样点Pk和Pk-1矢高的增量Δzk可以根据其y坐标的增量和δγk推导得出:

P0作为局部坐标系下的起始点,z1等于Δz1,再进一步求取z2,z3,…,z103,z104以及z-1,z-2,z-3,…,z-103,z-104。(www.xing528.com)

至此,可以获取各单视场单元对应的平面子镜的中心点坐标。从中心视场拓展到边缘视场,由中心点绘制的平面子镜基底的曲线轮廓如图11-31所示,即得到了用于f-θ畸变校正的各平面子镜中心点的相对位置信息。综合考虑不同孔径和视场采样下的特征光线,可以根据平面子镜基底的曲线参数获取每个平面子镜上全部离散点的坐标和法向量;然后,将其拟合形成曲面基底上多平面子镜融合型自由曲面校正反射镜。

图11-31　平面镜基底的曲线轮廓

在获取构成自由曲面校正反射镜的平面子镜参数后,其对应的离轴抛物面子镜单元的离轴角被更新,所以需要对这些离轴抛物面子镜单元进行重构和参数更新,然后再对坐落于离轴抛物面基底上的多离轴抛物面子镜单元进行扩展和融合,形成连续光滑的自由曲面,作为最终两反离轴远心扫描系统初始结构的主镜。每个“离轴抛物面-平面”子镜对均对应一个单视场单元,离轴抛物面子镜实现光束的会聚和远心度的控制,平面子镜实现畸变的校正,由此形成整个光路中的一段理想成像子光路。多面对融合型自由曲面主镜和校正反射镜分别是通过多离轴抛物面子镜和平面子镜的扩展和融合构建而成。

拼接融合型自由曲面校正反射镜和主镜的面型矢高分别如图11-32(a)和(b)所示,两个面型的有效孔径均为矩形,采用五阶XY多项式对其面型进行表征,其中,自由曲面校正反射镜的表征仅用子午平面内的XY多项式项,如y,y2,y3,y4和y5。

通过ZEMAX光学设计软件,对构建的两反离轴远心扫描系统的初始结构进行光学性能评估,成像质量如图11-33所示。在550nm的工作波长下,整个视场范围内,像面弥散斑半径的均方根为11.7μm,如图11-33(a)所示;最大f-θ畸变值略高于10μm,如图11-33(b)所示;像方远心角小于0.25°,基本满足像方远心条件,如图11-33(c)所示。

11.4.2.3　自由曲面两反离轴远心扫描系统的设计结果

基于多面对融合的设计理念,构建了两反离轴远心扫描系统的初始结构,还需通过光学设计软件进一步优化。由于自由曲面校正反射镜的面型构建是在子午平面内,为了辅助校正系统畸变,所以,将关于子午平面对称的XY多项式的项设置为优化变量。LEC为入瞳到自由曲面补偿镜的距离,初始为37.682mm,也将其设置为优化变量。

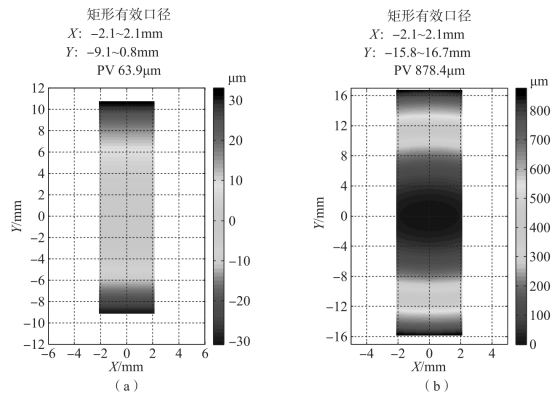
图11-32　两反离轴远心扫描系统初始结构自由曲面面型矢高

(a)校正反射镜;(b)主镜

图11-33　两反离轴远心扫描系统初始结构的光学性能(a)

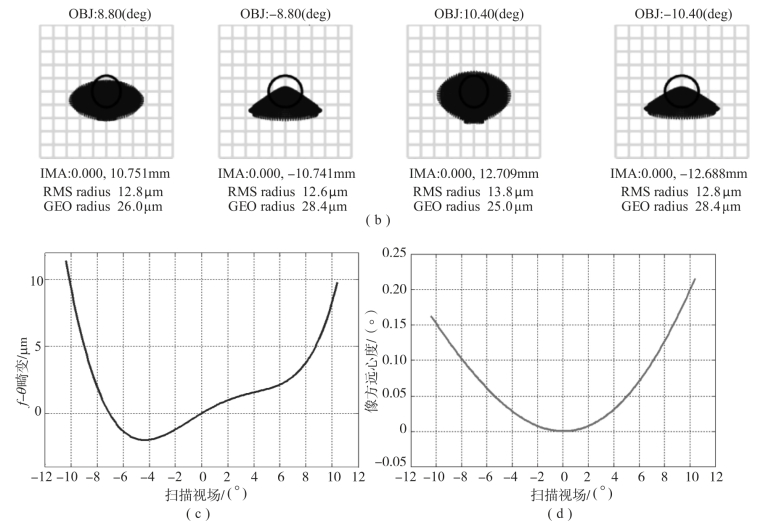
图11-33　两反离轴远心扫描系统初始结构的光学性能(续)

(b)像面弥散斑;(c)f-θ成像畸变;(d)像方远心度

优化后,两反离轴远心扫描系统结构的光路图如图11-34所示。单视场单元的弥散斑全部在艾里斑范围内,如图11-35(a)所示,根据视场与弥散斑RMS的曲线可以看出,整个视场范围的弥散斑均接近衍射极限;扫描范围内,最大的f-θ畸变值不超过5μm,如图11-35(b)所示;像方远心角小于0.2°,如图11-35(c)所示。

图11-34　线视场两反离轴远心扫描系统光路图

图11-35　两反离轴远心扫描系统最终的光学性能

(a)像面弥散斑;(b)f-θ成像畸变;(c)像方远心度

自由曲面主镜和校正反射镜的面型矢高如图11-36所示,其面型与图11-32初始结构中的面型矢高差别不大,优化后LEC为38.663mm。上述像质分析的结果表明,基于多面对拼接融合的设计理念建立的两反离轴远心扫描系统,具有理想映射关系的同时,满足像方远心条件,成像质量理想。

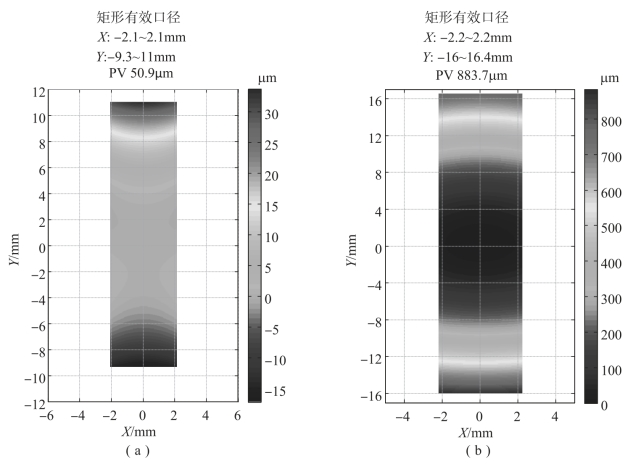
图11-36　两反离轴远心扫描最终系统自由曲面反射镜面型矢高

(a)校正反射镜;(b)主镜

在系统构建的过程中,通过两反的结构形式来完成设计,通过自由曲面主镜实现光束的会聚和远心度的控制,通过自由曲面校正反射镜实现畸变的校正,且对初始结构的优化过程并不影响该设计理念。表11-9给出了系统的具体参数,与商用扫描镜头相比,除了不引入色差的优势之外,离轴扫描系统的像方远心度得到提升。出于对自由曲面面型检测以及系统紧凑性的考虑,系统中不采用凸面反射镜,且工作距离为44mm,略短于商用扫描镜头54mm的工作距离。