基于无像差点曲面的微区分段拼接融合方法优化

上述三种直接设计方法,都是依据物像关系,直接求解得到自由曲面面型,没有考虑结构选型的合理性,也没有与光学系统几何特性和像差校正的理论相结合。经典的二次曲面包括椭球面、抛物面、双曲面,对于给定的物像关系,它们具有完善的无像差共轭点。比如,抛物面可以对无限共轭处完善成像、椭球面可以对有限共轭处完善成像。但这些二次曲面几何体的视场有限。本书作者所在的研究团队提出了一种应用于自由曲面光学系统设计的基于特征几何体的分段拼接融合方法,将全视场光学系统看作多个单视场或小视场子系统的分段组合,由离轴二次曲面构成的无像差经典结构直接生成各子系统。进一步,将各子系统单元的二次曲面分段拼接,并融合形成连续光滑的自由曲面,实现全视场光学系统初始结构的构建。设计过程由小视场到大视场,面型从简单至复杂。

以对无限远成像的像方远心自由曲面单反系统为例,图11-12为采用多离轴抛物面分段拼接融合方法构建自由曲面反射镜的设计理念示意图。按照图11-12中所示的视场范围,离散采样9个视场点,如果单反射镜如果能够满足完善成像条件,那么1～9个视场所对应的反射镜面区域均为离轴抛物面,称之为自由曲面的单视场分割子镜单元。在图11-12中,按照从像平面到入瞳的反向光路,各视场主光线构成的光路为平行光路会聚到入瞳中心。相应的,各视场主光线与自由曲面反射镜的交点构成的曲面也为离轴抛物面,即各抛物面子镜坐落在一个大离轴抛物面基底上。

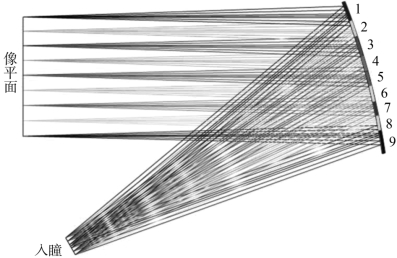
图11-12　多离轴抛物面分段拼接融合方法构建自由曲面单反射镜设计理念图

离轴抛物面反射镜作为准直镜,对于0°视场而言,无论孔径多大,离轴抛物面反射镜均可以完善成像于焦点处。但它在轴外现场无法做到完善成像,并且由于离轴抛物面的非旋转对称性,其对视场像差的容忍力较差。对于图11-12所示的全视场分割为多个单视场单元。其中,相邻视场的子镜面型存在重叠现象,或是单一子镜承接了来自多个视场的光束。所以,将各个离轴抛物面子镜单元拼接融合形成连续顺滑的自由曲面,其融合方法是核心问题。

根据单反射镜面的物像关系,包括入瞳直径、视场范围、像面大小等,可以计算出离轴抛物面基底和各离轴抛物面子镜的参数。尽管曲率半径、离轴角这些参数可以直接用于表征各小视场分割子镜单元,但拼接融合的过程无法直接对两面型表达式进行拟合,所以需将其看作是离散数据点集合。根据离轴抛物面的参数定义,可以获取反射镜面的特征点数据,根据各个反射子镜的特征点数据拟合形成自由曲面。传统的拟合方式只考虑坐标数据点进行拟合。但是,法线方向直接决定着反射光线的方向,法向数据比坐标数据更重要,它会使面型拟合更精确。因此,通过离轴抛物面的参数定义,计算特征采样点的坐标和法向数据,综合考虑坐标和法向的影响,拟合形成自由曲面。

然而,构成各离轴抛物面子镜单元上的离散点仅针对某一个采样视场,相邻离轴抛物面子镜单元在连接处矢高不同,重叠区域承接了两个视场的光束,连接处面型的不连续以及斜率的不相等会对融合造成障碍。针对此问题,本书作者所在的研究团队提出了一种以中心视场离轴抛物面子镜为基准,逐段调整相邻离轴抛物面子镜单元的方法,减小邻近子镜的矢高偏差,扩展生长融合自由曲面面型。离轴抛物面子镜单元的参数调整采用“旋转—平移” 两步法:将待调整的离轴抛物面子镜单元绕中心点旋转,再将旋转后的离轴抛物面子镜单元沿入射至其表面的主光线的方向平移,使相邻离轴抛物面子镜单元重叠区域的面型矢高差最小。尽管离轴抛物面子镜单元进行了调整,调整后的各离轴抛物面子镜中心偏离原先设定的大离轴抛物面基底,但旋转的角度微小,远心度偏差不大。上述方法目前已经在线视场系统中得到了应用,具体见11.4节的案例。

进一步分析多离轴抛物面融合型自由曲面单反射镜的成像特性,如图11-13所示,系统的线视场范围为±θ。顶部离轴抛物面子镜单元和底部离轴抛物面子镜单元分别对应+θ和-θ的视场,为图11-13中标示出的最顶端和最底端曲面,中央曲面表示0°视场对应的离轴抛物面子镜单元。它们对应的离轴角分别为β+θ、β-θ和β0,离轴量分别为D+θ,D-θ和D0,+θ和-θ的视场对应的像高分别用H+θ和H-θ表示,其符号相反。

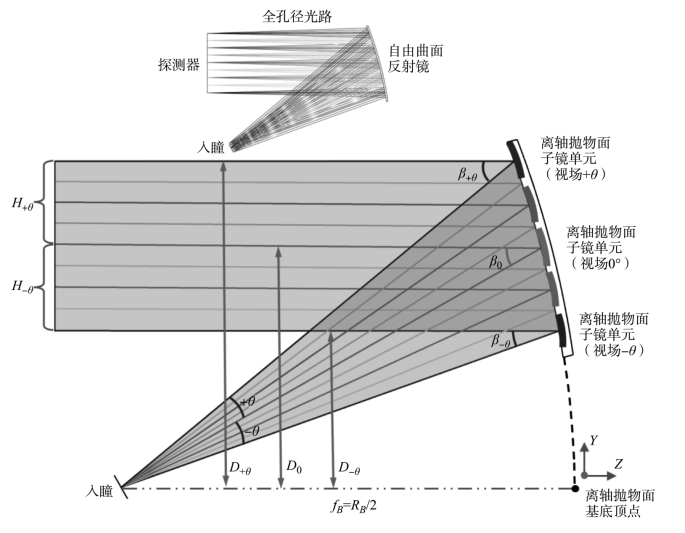
图11-13　多离轴抛物面融合型自由曲面单反射镜的成像分析

图11-14示意了一段包括0°视场对应的离轴抛物面子镜单元在内的细节光路。从入瞳到离轴抛物面子镜单元的主光线长度表示离轴抛物面基底上该位置处的反射焦距,对于0°视场,用表示。离轴抛物面子镜单元到像平面的主光线长度表示该离轴抛物面子镜单元的反射焦距,对于0°视场,用表示。0°视场对应的离轴抛物面子镜单元母抛物面的顶点位置和离轴抛物面基底母抛物面的顶点位置不同。离轴角β0的选取以单反射镜系统兼顾无遮拦和结构紧凑作为标准,离轴角β+θ和β-θ可以根据视场+θ和-θ以及离轴角β0的几何关系确定,它们之间存在如下关系:

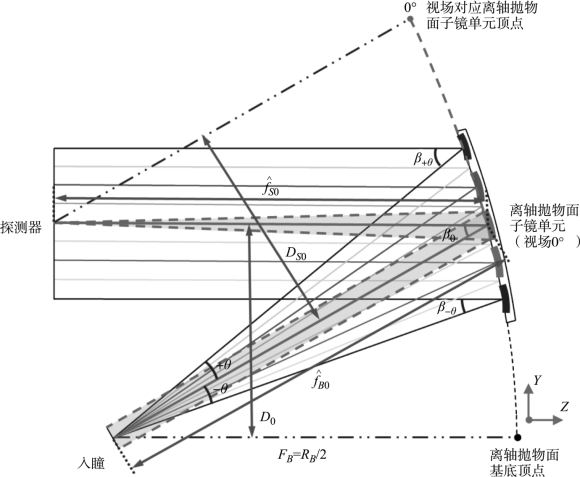
图11-14　离轴抛物面子镜单元参数细节图

光线从像平面到反射镜,再到入瞳中心的反向光路中,离轴抛物面基底使这些主光线理想会聚。因此,对于任意视场,从入瞳到像面所有主光线的光程是相等的。换句话说,对于每个离轴抛物面子镜单元,其反射焦距和位于离轴抛物面基底上该位置中心处的反射焦距之和是恒定的。因此,若设定0°视场离轴抛物面子镜单元的主要参数,如和,则可以推导出任意视场对应的离轴抛物面子镜单元的主要参数,它们之间满足

式中,和分别表示离轴抛物面基底在视场+θ和-θ处主光线的反射焦距;和分别表示视场+θ和-θ对应的离轴抛物面子镜单元的反射焦距。+θ和-θ视场的主光线经自由曲面反射镜反射后入射至像平面,对应的像高分别记为H+θ和H-θ,它们与离轴量D+θ,D-θ和D0存在如下的关系:

根据离轴抛物面主要参数之间的转换关系,可以得出(www.xing528.com)

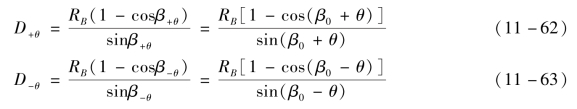
像高H+θ和H-θ分别表示为

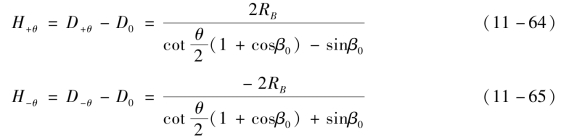
根据表达式可以定量得出,视场+θ和-θ对应的像高H+θ和H-θ除了符号相反外,其大小的绝对值也不同,其原因正是由于离轴抛物面基底不对称的几何特征所致。换句话说,多离轴抛物面子镜的分段拼接融合机制会对自由曲面单反成像系统引入不可避免的成像畸变,且畸变校正与远心度控制之间存在着相互制约的问题。因此,单个自由曲面反射镜难以同时满足像方远心控制和畸变的校正。

成像畸变是一种主光线像差,表征的是实际像高和理想像高之间的差值。根据系统焦距和视场,以及投影关系(f-θ或f-tanθ)可以直接计算获取理想高度。如图11-15所示,+θ和-θ视场对应的实际像高和理想像高分别为H+θ和H-θ,以及h+θ和h-θ。图11-15中,各视场的理想主光线用虚线表示。在经典结构中,牛顿望远镜就是利用平面镜来对光路进行折叠,根据这个设计理念,可以利用平面镜将主光线的方向偏折一个角度,从而入射至理想位置,实现畸变校正的同时,不会影响偏折前反射镜的会聚能力。

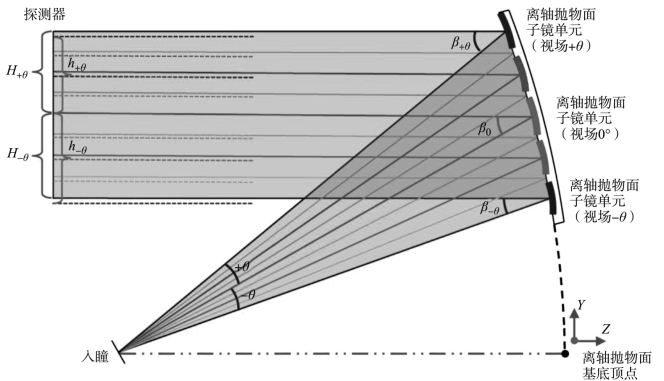
图11-15　离轴抛物面融合型自由曲面单反射镜的成像畸变

因此,可以在单自由曲面反射镜的基础之上,再增加一块校正反射镜。由多个离轴抛物面子镜单元拼接融合形成的自由曲面作为两反离轴远心扫描系统的主镜,使主光线的方向发生偏折的由多个平面子镜拼接融合形成的自由曲面作为两反离轴远心扫描系统的校正反射镜。两个自由曲面镜上,离轴抛物面子镜和平面子镜一一对应,形成由多个面对组成的两反成像系统。

如图11-16所示,有两个位置可以放置由多个平面子镜单元构成的校正反射镜,一个是在入瞳和自由曲面主镜之间,另一个是在自由曲面主镜和像平面之间。由多平面子镜单元构成的校正反射镜,类似于望远镜系统中校正球差的施密特校正板,但这种反射式自由曲面校正板主要用于校正系统中的畸变。

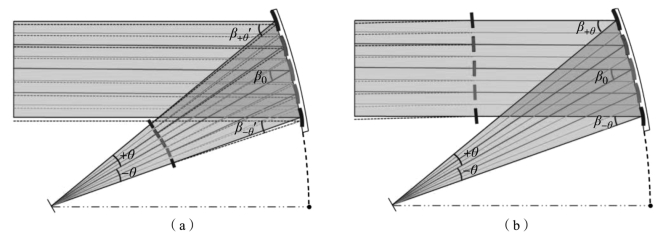
图11-16　多平面融合型自由曲面校正镜的设置方案

当自由曲面校正反射镜置于入瞳和自由曲面主镜之间时,如图11-16(a)所示,各视场光束在入射至自由曲面主镜前就发生偏折。所以,除了0°视场对应的离轴抛物面子镜单元外,其他离轴抛物面子镜单元均需要进行重构和参数更新。+θ视场对应的离轴抛物面子镜单元的离轴角由β+θ更新为角度更小的β′+θ,-θ视场对应的离轴抛物面子镜单元的离轴角由β-θ更新为角度更小的β′-θ。重构后,扫描视场角和离轴角之间的新对应关系可以有效改善系统的成像畸变。经重构后的离轴抛物面子镜单元的反射主光线仍互相平行,且保持了像方远心。

当自由曲面校正反射镜置于自由曲面主镜和像面之间时,如图11-16(b)所示,各视场光束经自由曲面校正反射镜反射后发生偏折,不影响主镜前后的光路。所以,多离轴抛物面子镜单元不需要进行重构和参数更新。然而,各视场的成像畸变是不同的,所以,自由曲面校正反射镜需要对自由曲面主镜反射后的主光线,针对每个视场偏折不同的角度来进行畸变校正。这会导致经自由曲面校正反射镜后的主光线互相不平行,破坏了系统像方远心性,即这种结构无法在校正畸变的同时保持像方远心。另外,该方案的系统工作距离短。

因而,自由曲面两反离轴远心系统的初始结构构建方案为:将全视场分割为多个单视场单元,每个单视场单元由一对平面子镜和离轴抛物面子镜构成理想成像的子光路,由此形成由多个面对组成的两反成像系统(图11-17)。离轴抛物面子镜实现光束的会聚和远心度的控制,平面子镜实现畸变的校正,从而达到无畸变远心成像的效果。融合各个离轴抛物面子镜形成自由曲面主镜,融合各个平面子镜形成自由曲面校正镜。

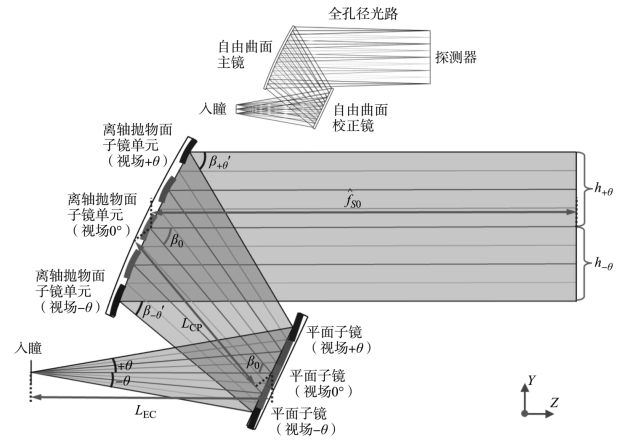
图11-17　多面对融合型两反离轴远心系统初始结构构建方案示意图

上述自由曲面单反和两反系统的构建,充分利用了二次曲面几何体的无像差特性。并且从单反结构往两反结构的演变,基于像差校正的需求,合理选择了两反的布局方案。目前提出的构建方案均针对远心成像关系,如光学系统对远心成像不做要求,亦可以根据相应的物像关系求解各个离轴抛物面子镜的结构参数。此外,目前的分段拼接融合方案仅考虑了与离轴方向相同的线视场,本书作者所在的研究团队正在继续开展研究工作,从线视场往面视场拓展,旨在进一步发挥基于特征几何体的分段拼接融合方法的优势,实现充分考虑像差校正要素的自由曲面光学系统初始结构的构建。