光瞳外置的目镜设计优化方案

目镜是光学系统中特点鲜明的光学系统,其结构选型与像差精准控制的方法很具有代表性,名为“目镜”,可以演变到光瞳外置的所有光学系统。通过对这一类光学系统设计方法的研究,对其余光瞳外置光学系统的设计具有重要的参考价值。下面我们以对称式光学结构与双胶合加单透镜的光学结构为例,来阐明其设计思想与像差校正方案。

9.3.2.1　目镜光学特性特点

目镜是一类特殊的光学系统,与人眼联用。作用:将物镜所成的像,通过目镜成像到无限远,供人眼观察。

(1)焦距短。对于望远镜用目镜,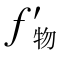=-,如大,则很快增加(因为≫1),为了减小体积,尽可能减小目镜的焦距。另外,目镜使用时,要求有一定的出瞳距离。对于显微镜用目镜,=,Γe一般在10×,～5mm。所以目镜焦距短。

(2)相对孔径比较小。目镜的出射光束直接进入人眼的瞳孔φ瞳=2～4mm,所以望远镜的出瞳孔径4mm(军用);显微镜(入瞳孔径小)的出瞳孔径1～2mm;而人眼焦距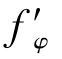=15～30mm,所以D/f′≤1/5。

(3)视场角大。

望远镜,tanω′=Γtanω,无论增加Γ,还是增大物方视场ω,都要增加ω′;显微镜,要增加物镜的线视场,也是相当于增加目镜物方焦面的线视场。用y′=f′tanω′,如目镜焦距f′一定,则ω′变大。视场大小如下:

一般视场角2ω′=40°

广角视场2ω′=60°

特广角2ω″=100°

(4)入瞳与出瞳远离透镜组。如图9-11所示,目镜的入瞳位于前方的物镜上,出瞳位于后方一定距离上。

图9-11　目镜的出入瞳情况

9.3.2.2　目镜的像差校正

目镜视场大:出入瞳远离透镜组,轴外光束在透镜组上的透射高较大,在透镜表面上的入射角自然很大,所以斜光束像差(彗差、像散、场曲、畸变、垂轴色差)很大,目镜的结构一般比较复杂。目镜焦距短,相对孔径比较小,目镜透镜组数比较多,所以目镜的球差、轴向色差一般不大,不用作刻意校正。

主要校正轴外像差(以影响成像清晰度像差为主):,,,,,,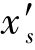。对于,目镜随着视场变大,都允许有较大的畸变。随视场变化,目镜允许的畸变关系如下:

2ω′=40°时,≤5%;2ω=60°～70°时,≤10%;2ω′＞70°时,可以大于10%。

目镜中场曲一般不进行校正。如要消场曲,必须正负分离或采用厚弯月型透镜,使光束进一步增大,但焦距不大,这样会使高级像差变得很大。即使用若干透镜组合,轴外像差如彗差、像散、畸变、垂轴色差也无法达到很好的校正,所以一般不校正场曲。目镜设计中应该校正,,,。

初级彗差和光束孔径的平方成比例。而目镜的出瞳直径较小,所以彗差不会太大,在这三种像差中居于次要位置。目镜设计对F光和C光消色差,对D光或e光校正单色像差。

设计目镜时,通常按反向光路设计,即入瞳在目镜的前方,在其焦平面上计算像差。

9.3.2.3　举例设计——对称式光学结构的目镜设计

设计要求:4×望远镜的目镜,f′=25mm;视场角2ω′=40°;出瞳直径D′=4mm;出瞳距离＞20mm;望远系统的入瞳与物镜重合;不考虑目镜结构和物镜之间的像差补偿。

按反向光路设计,设计要求转化为:

焦距:f′=25mm;

视场角:2ω=40°;(www.xing528.com)

入瞳直径:D=4mm;

入瞳距离:＞20mm;

出瞳距:≈100+20=120。

根据设计要求,系统的相对孔径为1/6.25,视场为40°,属于中等视场的物镜。可以选用对称式光学结构。

为了控制出入瞳距,在像方加入虚拟平面,控制出瞳距为120mm。

初始结构数据如表9-23所示。

表9-23　r、d参数与玻璃牌号

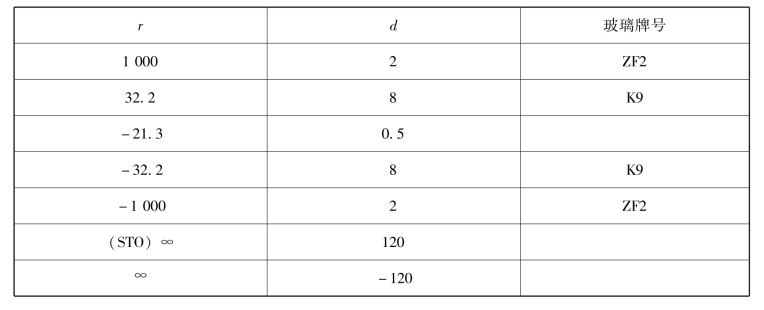
表9-22中倒数第二行,设置虚拟光瞳面,保证出瞳距离。

由于系统选用对称式结构,自变量只有三个曲率半径,所以只能校正三种像差,应该是f′,,。对于或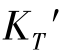,因相对孔径较小,彗差值不太大。

讨论一下像散的校正方案,像散校正方案有两种:①直接校正像散=0,则;②通过校正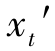=0,间接缩小,则。

这两种校正像散的方案得到的像差校正状态,如图9-12所示。

显然,由图9-12发现,第二种(b)校正状态比第一种(a)校正状态的轴外成像质量好。在目镜设计中,往往采用=0的像散校正状态,不采用=0的校正状态。需要

图9-12　光瞳外置系统校正像散的两种方案呈现的像差状态

(a)第一种校正像散的方案;(b)第二种校正像散的方案

注意:=0与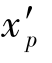=0的条件不一样,因为与hz、h都有关系,而只与φ有关。

所以,评价函数要体现校正f′=25mm,=0,=0。优化并归一化后,得到结构数据如表9-24所示。

表9-24　r、d参数与玻璃牌号

其像差结果如表9-25所示。

表9-25　对称式结构优化后的像差结果

通过计算几何像差的容限,可以判断表9-9中有关像差的校正效果。