许多红外透射材料具有较高的折射率,导致表面具有较小的矢高和较小的陡度,按照像差理论,可以显著地降低像差,尤其是高级像差。为了方便讨论得到这样的结论,图7-13给出6个通光直径为25.4mm的f/2单透镜,通过改变单透镜的弯曲程度获得最小球差。透镜的折射率取值范围为1.5~4.0,其中折射率1.5接近于常规BK7玻璃,而折射率4.0接近于锗。由图7-13发现,折射率为1.5时,透镜前表面陡峭外凸,后表面轻微外凸;折射率近似为1.62时,后面变为平面。随着折射率的增大,透镜变得越来越同心。
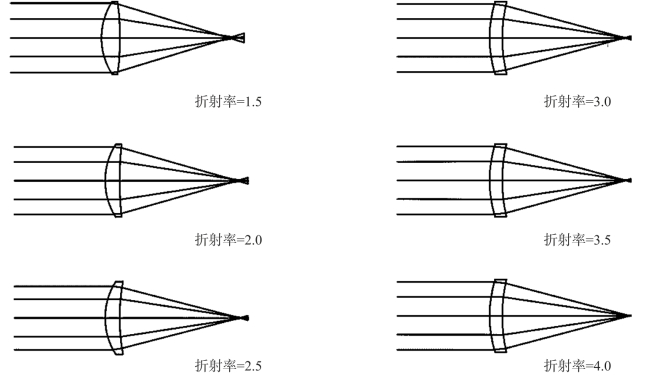
图7-13 实现最小球差的透镜弯曲与折射率的关系
图7-14给出了最小球差弯曲透镜的均方根波前误差(波长为0.5μm)随折射率变化的曲线。在折射率1.5处,均方根波前误差超过10个波长,峰谷波像差大约50个波长,球差表现非常大。
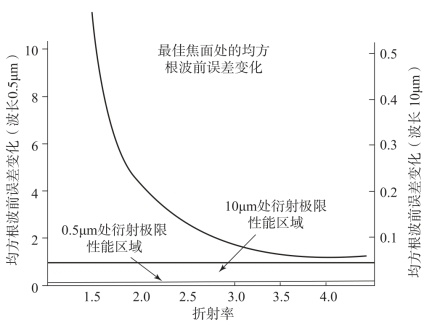
图7-14 直径25mm f/2透镜的球差与折射率关系
图7-14表现出,像差随折射率增大而迅速减小。在折射率为2.0处(该折射率是可见光玻璃中最高的),均方根波前误差大约有3个波长,峰谷波像差约为15个波长。在折射率为4.0处,均方根波前误差约为1个波长,峰谷波像差约为5个波长。可以看出,像差的减小很显著,但是,在折射率为4.0时,肯定会想到热红外波长的锗材料,因为普通玻璃不会具有这样高的折射率。在LWIR波段,需要改变曲线的纵坐标比例,以表示以10μm波长为单位的均方根波前误差。10μm波长是0.5μm可见光波长的20倍,需要将纵坐标值减小20倍,1个波长的均方根波前误差变成0.05个波长的均方根波前误差,近似为0.25个峰谷波长,已经满足瑞利判据,达到衍射极限。总结一下,直径为25.4mm的f/2玻璃单透镜在透镜的折射率为1.5(类似于BK7)时,其像差大约为50个可见光峰谷波长(是衍射极限的200倍);在透镜折射率为4.0的等效锗单透镜时,被弯曲成最小球差,以LWIR波段10μm波长度量,刚好满足瑞利判据,大约为0.25个峰谷波长。(https://www.xing528.com)
正因为如此,红外光学设计的形式,通常比可见光设计显得更加简单。单锗透镜足以满足直径25.4mm的f/2 LWIR镜头的要求;而在可见光波段,则需要三片单透镜才能达到衍射极限。
前已述及,一些红外材料具有很低的色散,因此通常不需进行色差的校正。为了说明这一点,假设一个虚拟的实验装置,如图7-15所示。实验装置中将一块棱镜放在距离垂直墙面2.5m的地方,用不同材料制作棱镜使得各谱段的中心以(45°-α)角向下偏折(α是棱镜角),然后测量可见光、MWIR和LWIR波段的最终长度。
图7-16给出了按照图7-15得到的实验结果。用于0.4~0.7μm可见光的高色散SF6玻璃有大约120mm的光谱长度,低色散的BK7玻璃有大约30mm的光谱长度。在3~5μm波段,硫化锌的光谱长度为35mm,硒化锌为17mm,硅为12mm。锗在MWIR波段的色散很大,其光谱长度为35mm。在LWIR波段,硒化锌的光谱长度大约为50mm,而锗的光谱长度为4mm。该值比任何其他材料的值都小得多,表明在LWIR波段使用锗,可不必进行色差校正。
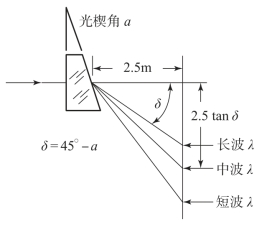
图7-15 不同材料光谱长度虚拟实验
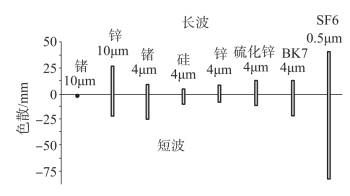
图7-16 离棱镜2.5m远墙上的光谱长度
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




