天文光学中的椭率问题

暗物质探测是天文光学的一个重要研究方向。暗物质是存在于宇宙中的一种不可见的物质,它占据宇宙中全部物质总质量的85%,对暗物质的观测可以帮助天文学家完善物理学理论体系,进而揭示宇宙的本质(图6-19)。但天文望远镜作为一种成像型光学仪器,无法直接观测宇宙中的暗物质,目前通过对弱引力透镜效应的观测实现暗物质的间接探测是暗物质探测的主流方法。

图6-19　星系形状的观测过程

椭率是天文光学中定义一个星系形状的重要参数。天文学家通过精确测量由弱引力透镜效应导致的天体椭率变化反推宇宙中影响光线传播路径的暗物质。宇宙中星系的本征椭率大约为0.3,由弱引力透镜效应造成的剪切量极小,大约为0.01。在对星系成像的过程中,除了弱引力透镜会影响星系成像的椭率外,天文望远系统自身的不完善成像也会导致像面星系椭率的变化。为保证弱引力透镜效应的观测准确度,必须在系统设计过程中控制并精确测量天文望远系统引入的椭率变化。因此,在天文望远系统设计中,定义光学椭率作为评估天文望远系统核心性能的新指标。

天文望远镜的常规像质指标有点列图、波像差、MTF、畸变等。此外,点扩散函数(PSF)也是反映望远镜成像质量的一项重要指标参数,根据PSF的分布可以计算半高全宽(FWHM)、椭率(e1,e2)、80%能量圈半径(EE80)以及等效噪声区(ENA)等性能指标。FWHM表征PSF的大小,椭率表征PSF的形状,椭率的特性是PSF随时间和空间而变化。望远镜的光学椭率是一项与暗物质探测科学目标密切相关的性能。光学系统的PSF与光瞳孔径函数和系统波像差两个因素相关,定义如下:

式中,P为光瞳函数;A为光瞳孔径函数;OPD是望远镜系统的光程差。

利用精确的光学PSF模型可以对椭率的特性进行建模和分析。采用天文光学中表示星系各向异性的KSB+方法:

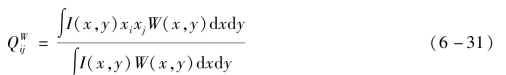
式中,I(x,y)是PSF的强度,W(x,y)是比例长度的高斯权函数,比例长度是描述PSF弥散大小的一种度量,例如半光半径(half-light radius),且有xi=x-,xj=y-。椭率e和它的大小R由下式定义:

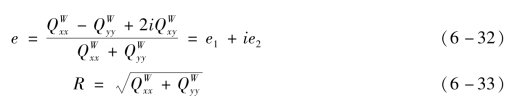(www.xing528.com)

椭率的计算受制于采样范围、采样距离和高斯半径,采用不同的采样范围和距离、高斯半径,会获得不同的结果,因此可根据实际情况采取相应的值。

由式(6-30)可知,PSF与望远镜的像差相关,因此,光学椭率与光学系统的像差大小与成分相关。已有研究表明,7种初级像差中,对称特性像差都不会影响椭率的大小,而失去对称性的像散和彗差则直接影响系统的椭率。高阶彗差是系统中光学椭率的主要来源,像散对椭率的影响取决于系统的离焦量,离焦量越大,像散对于椭率的影响越明显,若系统不存在离焦,则系统中不存在由像散引入的椭率。图6-20为一个离轴反射式望远镜系统的全视场波像差RMS值分布图与全视场椭率大小分布图,两者分布特征接近,可以看出波像差椭率存在一定的相关性。因此,可以通过在设计过程中控制失对称像差以及限制波像差大小来实现降低光学椭率的目的。

一个良好的天文观测系统,对全视场椭率的大小、空间稳定性和时间稳定性都有着非常严格的要求,以满足对于暗物质探测的需求。观测系统需要满足以下指标:

(1)全视场椭率均小于0.15;

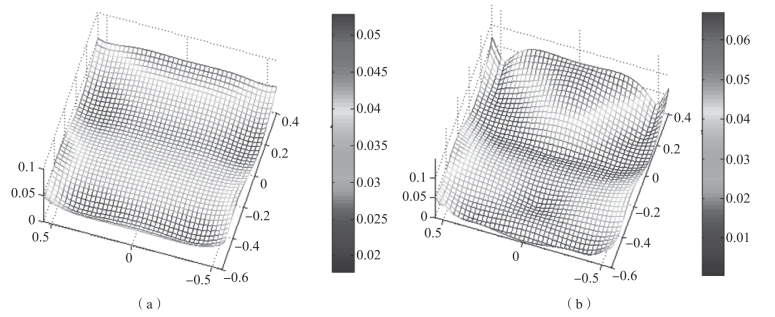
图6-20　某一望远镜系统的分布图

(a)全视场波像差RMS值分布图;(b)全视场椭率分布图

(2)探测器上椭率的插值误差小于2×10-4;

(3)两次连续曝光之间,椭率变化量小于5×10-3。

为了能对宇宙中暗物质和暗能量开展探测和研究,近年来各国争相开展大科学计划。欧洲航天局计划在2020年左右发射欧几里得空间望远镜,我国计划在2022年前后发射中国空间站望远镜。面向天文望远镜暗物质探测的科学目标,光学椭率是一个全新的光学设计指标,在光学系统设计时光学椭率被纳入评价范围,也对天文光学系统的设计提出了新的要求。