探讨成像基本概念

像质要求达到衍射极限的光学系统,使用几何光学方法往往得不到正确的评价,需要用关于衍射理论的衍射成像方法。

6.1.2.1　点扩散函数

点扩散函数(Point Spread Function,PSF)指一个理想的几何物点,经过光学系统后像点的能量展开分布。如物点经光学系统成像的辐照度分布为h(x′,y′):

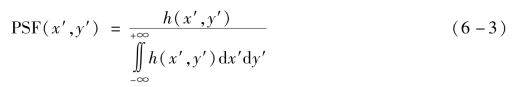
真实的点扩散函数应该利用惠更斯(Huygens)原理进行计算,也可用快速傅里叶变换(FFT)算法进行近似计算。

光学系统像面上光振动的复振幅相对分布为ASF(x′,y′):

其中,ASF(x′,y′)与光学系统光瞳函数P(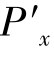,)具有如式(6-5)的关系:

式中,(,)为出瞳上的坐标;R是出瞳到像平面的距离;P(,)为光瞳函数,与光学系统波像差W(,有关。

式中,A(,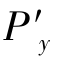)为振幅分布函数,描述光瞳面上光透射均匀与否。当为均匀透射时,A(,)=1。

6.1.2.2　圆内能量集中度

对于小像差光学系统,可以由点物所成点像的能量集中程度来表示,能量百分比随点像弥散圆半径之间的变化关系称为圆内能量集中度(Encircled Energy,EE)。假如,CCD传感器作为像接收器,其像素间距为7.5μm,则对光学系统简单又可靠的像质评价方法就是点物目标的80%能量应落入7.5μm的直径之内。图6-4给出了柯克三片型的圆内能量集中度曲线,能量的80%包含在大约6μm的直径范围内。PSF和EE在现代光学设计软件中都能被计算给出。

6.1.2.3　衍射像

若光瞳函数是常数,即系统消像差,系统的透过率在整个圆孔瞳面上是一致的,则点像的强度分布为

图6-4　圆内能量集中度曲线

式中,I0=I(x′=0,y′=0),为轴上点的强度;J1为一阶贝塞尔函数,表达式为

m是规划的像面极坐标。

贝塞尔函数Jn(x)的基本定义用积分表示:

其递推关系为

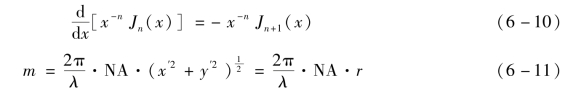
落在离开衍射斑中心距离r0内的能量(总能量的百分数)为

式中,m0=·NA·r0;J0(x)为零阶贝塞尔函数,

(www.xing528.com)

式(6-7)的结果示于图6-5,它显示出衍射图的外貌。图的中心为艾里斑,斑的周围环绕着能量急剧减小的圆环。图6-6表示不同间隔的两个点像衍射图,虚线表示各自的衍射图,实线表示衍射图的叠加。表6-1给出了完善透镜圆孔和矩孔的能量分布。

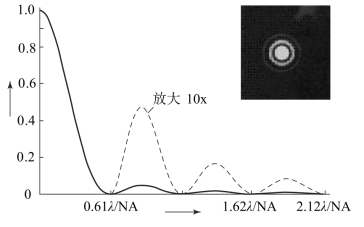
图6-5　衍射图的外貌

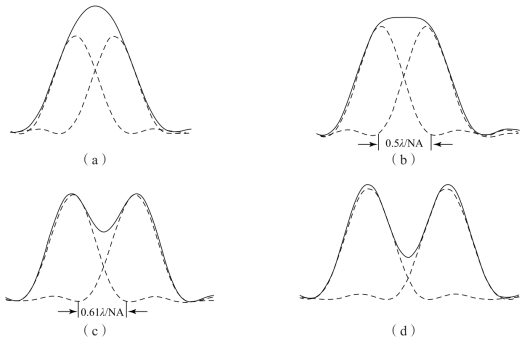
图6-6　不同间隔的两个点像衍射图

表6-1　完善透镜圆孔和矩形的能量分布(表示成离开衍射图中心距离r的函数)

续表

若为矩形孔时,

式中,α=2π·NA·x′/λ,β=2π·NA·y′/λ。

6.1.2.4　分辨率

当叠加的衍射图可以认为是两点而不是一个点时,可以说这两个点光源(或点物)能被分辨。两点不同距离时,叠加衍射图的变化如图6-6所示。

瑞利(Rayleigh)判据认为,若一个衍射斑的第一暗环与另一衍射斑中心重合时,那么两个点源刚好能被分辨,分辨率定义为

斯帕罗(Sparrow)认为可分辨的两点距离,是当叠加衍射斑在两点衍射斑之间没有最小值时,分辨率为

对于有限共轭距的成像关系,像方分辨距离可以转化为物方分辨距离,用像方分辨距离除以系统放大率。

对于无穷远目标成像,有时用物空间两物点的分辨角表示分辨率:

式中,D为光学系统入瞳直径,对于目视观察系统,当D以毫米表示,分辨角用角秒表示时,则上述分辨角分别约为140/D和115/D。

此处分辨率是理想光学系统可获得的,它们常被用于设计和制造优劣的标准,一个达到瑞利判据的系统有时称为衍射极限系统。

6.1.2.5　切趾法和变迹法

图6-5、图6-6所示的衍射图是假设系统理想,没有像差,具有均匀透过率的光瞳。如果光瞳面上透过率式(6-6)中的A(,)不是常数,则需要修正衍射图样。方法有两种:一种是减小次极大的光能,增加主极大(艾里斑)的光能;另一种是减小艾里斑的大小。例如,通过镀制的非均匀吸收膜,使光瞳上从中心到边缘透过率越来越小,结果是艾里斑直径稍有增加,但亮环中心光能减少,次极大被切掉,这是第一种方法,称为切趾法,适用于观察亮度相差很大的相邻物体,可提高对比度以提高分辨率。如图6-7(a)所示。

图6-7　改变艾里斑大小的方法

(a)切趾法;(b)变迹法

通过将光瞳变成中心被挡住的环形。此时减小了光瞳中心的透过率,结果是次极大更亮,但艾里斑的直径减小,这是第二种方法,称为变迹法,适用于观察同等亮度高对比的细小物体,可提高分辨率,如图6-7(b)所示。