平行玻璃板的初级像差公式优化

前面讨论了薄透镜系统和薄透镜组的初级像差。薄透镜系统因转像、缩短尺寸、分光等需要,还会包含分划板、测微平板、保护玻璃、盖玻片、反射棱镜、分光棱镜或平板玻璃等。反射棱镜与分光棱镜展开后,相当于一定厚度的平行玻璃板。

平行平板用于会聚或发散光路中,总会造成像的侧向位移,如图5-14所示。无限远物体发出的平行光束经会聚透镜L后应成像于A点,中间含有平行平板时,将成像于A′点,侧向位移Δl′,由式(5-25)计算:

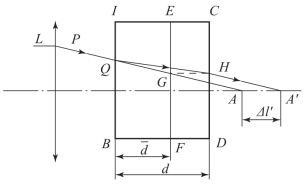
图5-14　平行平板的侧向位移

式中,d为平行平板厚度。

平行平板用于会聚(或发散)光路中时,会引起附加像差,这些像差平行平板无法消除,只有依靠有焦系统补偿消除。

图5-15给出了平行平板玻璃位于有焦系统中时第一辅助光线和第二辅助光线的光路情况。

图5-15　平行平板中光路情况示意图

玻璃板的厚度为d,玻璃的折射率为n,阿贝数为γ,第一辅助光线与光轴的夹角为U,第二辅助光线与光轴的夹角为Uz,式(5-26)～式(5-32)给出平行平板的7种初级像差方程组。

(1)球差:

(2)彗差:

(3)像散:

(4)场曲:

(5)畸变:

(6)轴向色差:(www.xing528.com)

(7)垂轴色差:

式(5-26)～式(5-32)清晰地说明:

(1)平板玻璃在有焦光路中引起的附加像差与厚度d、折射率n、色散系数γ以及光束的孔径角U、视场角Uz大小有关,U、Uz越大,附加像差越大,且球差、像散为负。

(2)附加像差大小与平板玻璃在光轴上的轴向位置无关。

(3)平板玻璃不产生附加场曲。根据以上结论,如果在同一空间中,有相同材料的若干块玻璃板,则可以合成在一起进行计算,它的厚度等于各块玻璃板厚度之和,玻璃板的位置可以任意给定。

如果平行平板倾斜置于旋转对称光路中,如图5-16所示,则光学系统就不再旋转对称,其结果是轴上视场位置,存在视场像差,比如彗差、像散、垂轴色差。引入的附加像差大小与垂直于光轴放置有所不同,尤其像散是引入的最严重像差。其余球差、场曲、轴向色差等同式(5-26)、式(5-29)、式(5-31),不同之处由式(5-33)～式(5-35)描述。

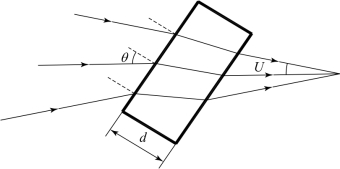
图5-16　倾斜θ角的平行平板

式中,θ为平行平板的法线与光轴的夹角,如θ=0°,表示垂直放置,因倾斜引入的附加像差消失。由式(5-33)～式(5-35)可以看出,如果平行玻璃板倾斜θ放置于会聚光路中,即使没有轴外第二辅助光线的作用,仅考虑轴上一定孔径角U的光束(近似有f/#=1/(2sin U)),也会产生严重的像散、彗差与垂轴色差。

假设有一个衍射极限的f/1.0镜头,其会聚光束被分成两束,一束折转90°被第一平面反射;另一束通过倾斜的平板分束器。反射光束从平板反射后没有变化,但透过光束却具有由倾斜平板产生的像散,平板越厚,存在的像散越大。

为了给出影响像散的直观情况,不失一般性,倾斜平行玻璃板材料为德国肖特公司的BK7,用弥散斑直径,描述因平板倾斜45°(一般分光镜的工作姿态)引入的像散(图5-17)随平板厚度d、透镜f/D的变化关系曲线。

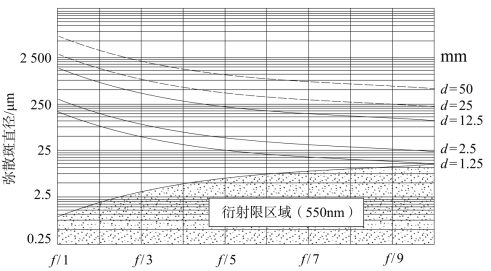
图5-17　三级像散弥散斑直径(单位为μm)与45°倾斜BK 7平板的厚度和镜头f/D的关系

倾斜平板在光学系统中引入的最为严重的像差是像散。但在某些情况下,即使平行平板厚度小于1mm,彗差和垂轴色差也是非常明显的。与前述相同,在平行平板倾斜45°,残余子午彗差引起的弥散斑与平板厚度、镜头f/#的关系如图5-18所示,垂轴色差引起的弥散斑与平板厚度、镜头f/#的关系如图5-19所示。由图5-19可以发现,垂轴色差与f/#无关,因为垂轴色差是主光线像差,仅与不同波长主光线的高度有关。

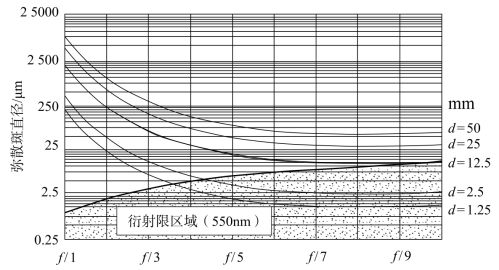
图5-18　子午彗差弥散斑直径与折射率1.5的倾斜BK 7平板的厚度和镜头f/D的关系

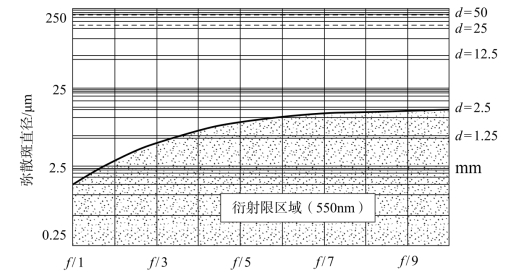
图5-19　垂轴色差弥散斑直径(单位为μm)与倾斜BK7平板厚度和镜头f/#的关系