孔径光阑远离单透镜的彗差规律解析

由式(5-16)得出,单透镜时,彗差与第二辅助光线的入射高度hz呈线性关系,从几何关系可以判断,hz与光瞳位置(如入瞳位置、出瞳位置)呈线性关系,因此彗差与光瞳位置也呈线性关系。让彗差SⅡ=0,则hz=JW/P。图5-7给出了常见形状的单透镜彗差随入瞳位置的关系图。由图5-7可以看出,不同形状单透镜的0彗差光瞳位置是不一样的。

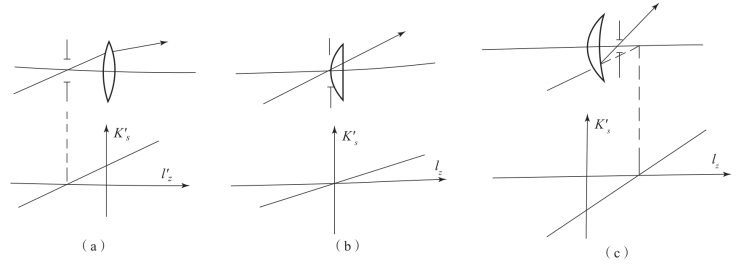
图5-7　不同形状透镜的彗差随光瞳位置变化关系

(a)双凸透镜;(b)平凸透镜;(c)正弯月透镜

对于凸面迎向平行光的平凸单透镜,其彗差为0的光瞳位置就是与透镜重合,这与图5-6、表5-2得到的结论相同。

为了表现光瞳位置对单透镜彗差的影响规律,在ZEMAX上,分别建立凸面迎向平行光的平凸透镜、双等凸透镜、正弯月透镜的系统数据,建立入(出)瞳距分别为0、5mm、10mm、15mm、20mm的多重结构,通过Spot diagrams中的Configuration matrix,给出点列图随视场、入瞳距的变化阵列。

图5-8为平凸透镜的多视场点列图随光瞳位置的变化关系阵列。

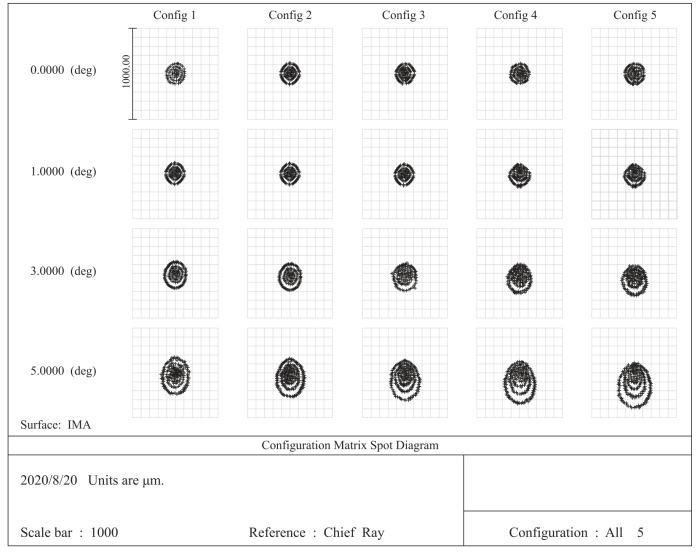
图5-8　平凸透镜的多视场点列图随光瞳位置的变化关系阵列(www.xing528.com)

图5-8左边为0°、1°、3°、5°。顶部的Config 1～Config 5表示5个多重结构,其中Config 1对应入瞳距为0,其余对应5mm、10mm、15mm、20mm。点列图中第一列彗差最小,即几乎无彗差,对应入瞳距为0,这与图5-7(b)中显示的彗差情况一致。

图5-9给出了双等凸单透镜与图5-8相同视场、相同入瞳距情况下的点列图分布。由图5-9看出,随着入瞳距由0到20mm增大时,点列图的彗差成分越来越小,最右边一列(对应出瞳距20mm)点列图,其随光瞳孔径高变化的点列图环带同心度很好,表明此时彗差接近于0,这与图5-7(a)中显示的彗差情况一致。

图5-10给出了凸面迎向平行光的正弯月透镜的点列图随着视场与入瞳距的变化。

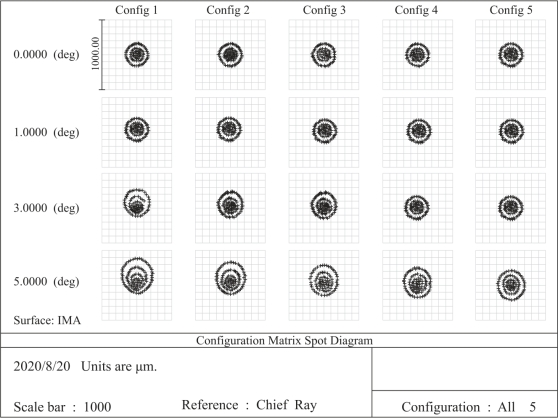
图5-9　等凸透镜的多视场点列图随光瞳位置的变化关系阵列

图5-10　弯月正透镜的多视场点列图随光瞳位置的变化关系阵列

图5-10中视场设置与图5-8一致,具有0°、1°、3°、5°4个视场。5个多重结构Config 1～Config 5对应出瞳距0、5mm、7.5mm、10mm、15mm。图5-10中多重结构Config2、Config4在5°视场的点列图,其弥散圆偏心方向刚好相反,表明出瞳距5mm与10mm的彗差符号相反。为了找到0彗差的出瞳位置,结构Config3,对应出瞳距7.5mm,是专门设立的。可以看出,出瞳距7.5mm时正弯月透镜彗差近似为0,这与图5-7(c)中显示的彗差情况一致。