物品在无限远处，光瞳透镜上的彗差规律

根据式(5-16),光瞳与透镜重合时,hz=0,彗差SⅡ=-JW,像散SⅢ=J2φ。图5-6给出了f′=50mm、D/f′=1/4的单透镜在视场角0°、1°、3°、5°情况下的点列图(Spot Diagrams)。

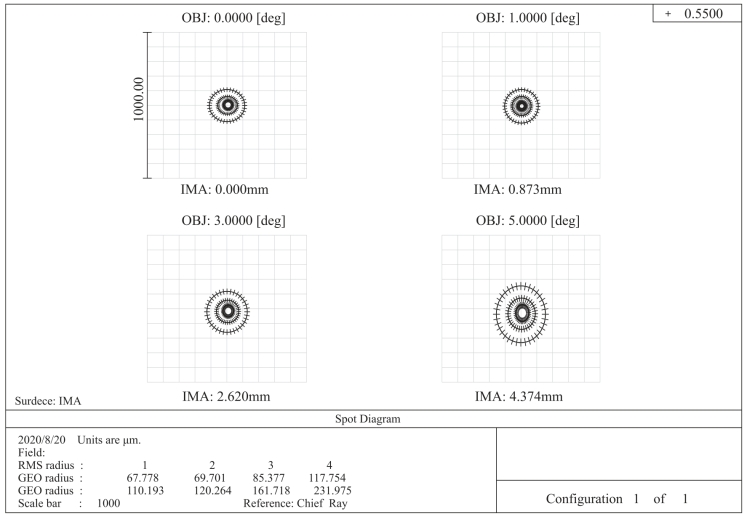
图5-6　光瞳位于平凸单透镜上的系统点列图

由图5-6发现,当物平面位于无限远、光瞳与平凸单透镜重合时,随着视场的增大,在3°视场内,轴外物点的像差成分与轴上物点一样,球差占主要成分,具有几乎相同的成像缺陷。即使到了5°视场,表现的像差成分仍然是球差,出现了明显的像散。(www.xing528.com)

表5-2给出了与球差、彗差、像散对应的Zernike多项式系数随视场的变化情况,也给出了与图5-6一样的像差演变现象。

表5-2　平凸单透镜Zernike多项式像差系数随视场的变化关系

依据上述在ZEMAX中的仿真结果可以得出结论,当光瞳与单透镜重合时,在一定的小视场范围内,轴外物点与轴上物点具有相同成像缺陷,称之为“等晕成像”。如果球差被校正到0,则轴外虽然彗差与光瞳无关,并不为0,等于-JW。但依据式(5-11)、式(5-12),视场较小时,轴外物点的物像方光线偏折角与轴上物点相比,变化不大,在P=0时,W≈0,因此彗差也不大,仍然满足等晕成像。随着视场的增大,轴外物点对应的像高不断变大,y′=f′tanω,像散=y′2,随像高y′的平方增加,表现出较大的像散。