物位于无限远时球差随透镜形状的变化规律

为了讨论单透镜球差随透镜形状的变化规律,使球差量值具有可比性,在ZEMAX软件平台上,保持焦距与相对孔径不变,建立平凸透镜、双凸透镜、正弯月透镜的光学系统,在可见光单一波长(λ=0.55μm)、焦距f′=50mm、D/f′=1/4下,计算出系统的球差数据(曲线),并做如下比较:

(1)凸面朝向平行光与平面朝向平行光的平凸透镜球差数据。

(2)双凸透镜在等凸、曲率半径绝对值前大后小、前小后大情况下的球差值。

(3)正弯月透镜在凸面弯向平行光的球差值。

(4)正弯月透镜在凹向平行光的球差值。

在此基础上,对单透镜的球差变化规律做总结,给出结论。

图5-3给出了相同光学特性参数下的平凸透镜球差数据。

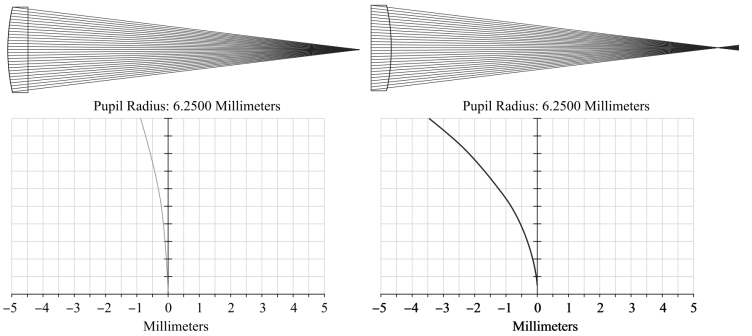
图5-3　平凸透镜的会聚性能与球差状况比较(www.xing528.com)

由图5-3可以看出,凸面迎向平行光的会聚性能优于平面迎向平行光;二者的球差值都是负的,满足正透镜产生负球差的规律,最大球差均出现在边缘孔径;前者边缘孔径球差为-0.86mm,后者边缘孔径球差为-3.44mm。因此,在相同条件下,优选选用凸面朝向平行光的光路安排,具有较小的会聚点和能量集中度。

图5-4给出了双凸透镜在相同光学特性参数下的会聚性能与球差曲线。由图5-4可以看出,曲率半径为51.34mm的等双凸透镜对平行光的会聚情况与球差大小,介于凸面迎向平行光的平凸透镜与平面迎向平行光的平凸透镜之间,其边缘孔径球差为-1.25mm。当前表面曲率半径变大,由51.34mm变成60mm时,为了保持焦距不变,后表面曲率半径变成-44.873mm,此时边缘孔径球差为-1.453mm;如果前表面曲率半径进一步增大,则会聚性能与球差演变情况向平面迎向平行光的平凸透镜逼近,即随着前表面形状越来越平,会聚性能越来越差,边缘孔径球差绝对值越来越大。当前表面曲率半径变小,由51.34mm变成40mm时,为了保持焦距不变,后表面曲率半径变成-71.799mm,此时边缘孔径球差为-0.961mm。如果前表面曲率半径进一步减小,则会聚性能与球差演变情况向凸面迎向平行光的平凸透镜逼近,即随着前表面形状越来越凸,会聚性能越来越好,边缘孔径球差绝对值越来越小。

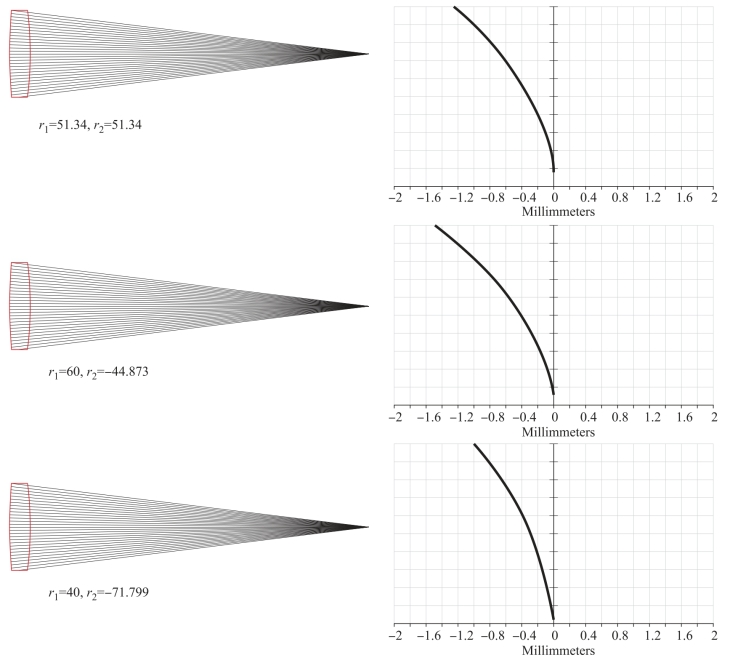
图5-4　双凸透镜的会聚性能与球差状况比较

图5-5给出了相同光学特性参数下正弯月透镜凸向平行光和凹向平行光的会聚性能与球差曲线,所用图片都在同一比例尺下。

图5-5中,对于凸面迎向平行光情况,随着透镜形状由近平凸向弯曲度越来越大方向发展,会聚性能越来越差,边缘孔径球差为负球差,绝对值越来越大。图5-5中第一行右边弯曲度较大的弯月透镜,曲率半径分别为8.5mm、10.089mm,边缘孔径球差达到-17.94mm。对于凹面迎向平行光情况,通过与左边相同形状弯月透镜相比,它们的会聚性能明显差于凸面迎向平行光方向的相同弯月透镜,边缘孔径球差明显变大。图5-5中最后一个透镜(凹面迎向平行光)的曲率半径分别为-22.16mm、-12.5mm,其边缘孔径球差达到-15.89mm,而同款透镜在凸面迎向平行光时的边缘孔径球差只有-5.60mm,小了近3倍。

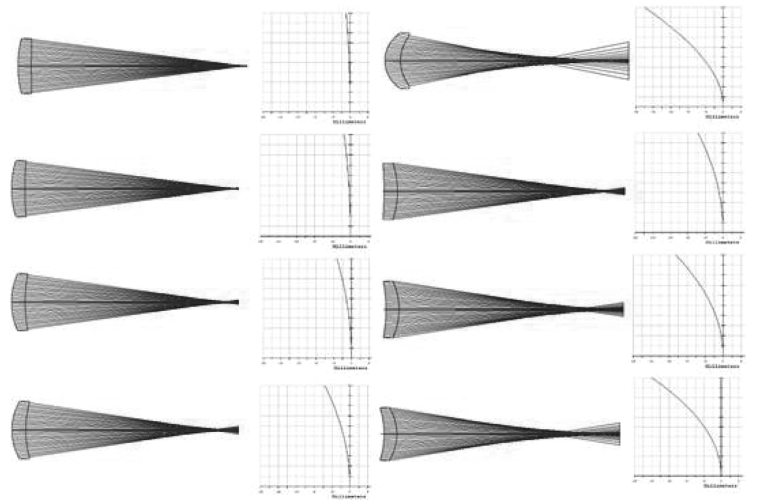
图5-5　正弯月透镜的会聚性能与球差状况比较

根据以上对单透镜对物平面位于无限远成像的轴上点球差讨论的结构看,凸面迎向平行光的平凸透镜产生的球差最小,这与用初级像差方程组的PW法求解透镜结构参数得到的结论一致(由于篇幅受限以及PW法的实用价值在衰退,因此本书对PW法不再赘述)。需要强调的是,对于无穷远的物点成像或者对平行光再聚焦,手边现有的单透镜,无论是平凸、双凸、弯月形状中的哪一种形状,实际使用时,选择凸面迎向物点或平行光这种光路方案效果最佳。