薄透镜组的单色像差特性优化为：薄透镜组的单色像差特性分析

5.3.1.1　一个薄透镜组只能校正两种初级单色像差

由初级像差公式可知,对于单薄透镜组,5个单色像差方程(5-1)～(5-5)变为

由式(5-15)～式(5-19)可以看出,对于单薄透镜组,有5个方程,但只出现2个单色像差参数。不管薄透镜组的结构怎样,只要只有一个薄透镜组,因只有两个单色像差参数P、W,最多只能满足5个方程中的2个,因此,一个薄透镜组最多只能校正两种初级单色像差。

换句话说,我们在光学设计时,一个薄透镜组不论它有多少自变量,如一个薄透镜组可能由多片透镜组成,此时具有多个曲率半径和玻璃光学常数(折射率),可以作为自变量用,但只要它们仅构成一个薄透镜组,就不能校正两种以上的初级单色像差(不包括高级像差)。

5.3.1.2　光瞳位置对像差的影响

当薄透镜系统中各个透镜组的光焦度、间隔不变,只改变孔径光阑(光瞳)的位置时,则初级像差方程组中的h、P、W都不变,而hz改变,从而引起像差的改变。

(1)球差与光瞳位置无关。在关于SⅠ的式(5-1)中,右边没有出现hz,球差显然与光瞳位置无关。

(2)彗差与光瞳位置有关。对于单薄透镜组,球差为0时,彗差与光瞳位置无关。

在关于SⅡ的式(5-2)中,出现了与hz有关的项。因此,一般来说,彗差与光瞳位置有关。但是,如果该薄透镜系统只由一个薄透镜组与一个孔径光阑构成,当球差为0(一般设计首先将球差校正到0),则对应P=0,由式(5-16)可知,SⅡ=JW,与hz有关的项消失,则彗差与光瞳位置无关。

(3)像散与光瞳位置有关。对于单薄透镜组,当球差、彗差都为0时,则像散与光瞳位置无关。

由式(5-3)表示的SⅢ,显然像散与光瞳位置(hz)有关。对于由单薄透镜组和孔径光阑构成的薄透镜系统,由式(5-15)、式(5-16),当球差、彗差等于0时,则P=W=0,代入式(5-17),SⅢ=J2φ,其中拉格朗日不变量J≠0,薄透镜组的光焦度φ≠0,此时像散与光瞳位置无关,是一个常数。(www.xing528.com)

对于上述像差与光瞳位置无关的情形,如果我们将入瞳或光阑位置作为一个自变量加入像差校正,实际上并不增加系统的校正能力。

(4)当光瞳与单薄透镜组重合时,像散为一个与透镜组结构无关的常数。

由式(5-17)可以看到,如果某个透镜组hz=0,则该透镜组的像散值为

由式(5-20)可见,此时像散由薄透镜组的焦距f′和像高y′所决定,与透镜组的结构无关。

(5)当光瞳与单薄透镜组重合时,畸变等于0。

由式(5-19)可知,如果hz=0,则SV中,与该薄透镜组对应的各项均为0。

(6)单薄透镜组的Petzval场曲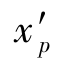近似为一个与结构无关的常量。

由式(5-18),得到单薄透镜组的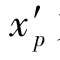为

前面已经阐明,μ对薄透镜组来说,近似为与结构无关的常数,等于0.7,由式(5-21)看到,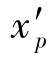显然应该是一个与结构无关的常数。