广义像差和结构参数的隐含函数关系

首先需要明确,光学自动设计过程,起步必须找到或建立作为设计起点的初始结构,作为变量的是初始结构的结构参数,包括描述光学面面型的顶点曲率半径、非球面系数、面后面的光学材料折射率(或牌号)、面间距离。

在光学自动设计中,对系统的全部要求,根据它们与结构参数的关系不同,划分成两大类。

第一类是不随系统结构参数改变的常数,如物距L,光束孔径高H或物像方NA,视场角ω或物高y,入瞳或孔径光阑位置,等等。在计算与校正光学系统像差的过程中,这些参数永远保持不变,它们是和自变量(结构参数)无关的常量。

第二类是随结构参数改变的参数,包括代表系统成像质量的各种几何像差或波像差,同时还包括某些近轴光学特性参数,例如焦距f′、放大率β、像距l′、出瞳距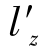、系统总长等。

为了简单方便,我们将第二类参数统称为“像差”,因为这里的像差与第2章介绍的像差概念不一样,可以称之为“广义像差”,用符号F1,…,Fm代表。系统的结构参数变量用符号x1,…,xn代表。两者之间的函数关系,如式(3-1)所示。

式中,f1是广义像差F1与自变量x1,x2,…,xn的函数关系,f2是广义像差F2与自变量x1,x2,…,xn的函数关系;fm是广义像差Fm与自变量x1,x2,…,xn的函数关系。这里的函数关系,是一种隐晦且无法用显式函数表示的函数关系。

式(3-1)是一个十分复杂的非线性方程组,我们称之为像差方程组。

光学自动设计问题,从数学角度看,就是建立和求解这个像差方程组,总体思路为:根据系统要求的像差值F1,…,Fm,从上述方程组中找出x1,…,xn的解,就是要求的结构参数。

但是,实际问题十分复杂,主要表现在:

(1)光学系统千变万化,系统像差与结构参数的函数关系千变万化,而我们讨论的方程组求解方法应该具有普适性。

(2)即使对某一具体系统,也根本找不出函数f1,…,fm的具体形式,当然就谈不上如何求解这个方程组了。

老一辈的研究人员手工计算的方案:在确定初始结构并满足第一类光学特性参数的前提下,用数值计算的方法求出对应的广义像差函数值F1,…,Fm,如果像差不满足要求,则依靠设计者的经验和像差理论知识,对系统的部分结构参数进行修改,然后重新计算像差,这样不断反复,直到像差值满足要求为止。(www.xing528.com)

电子计算机出现后,立即被引入到光学设计领域,用它来计算像差,计算速度得到了极大的提高。但结构参数修改仍然依靠设计人员来确定。随着计算机运算速度的提高,计算像差所需的时间越来越少。此时,人们很自然想到能否让计算机既计算像差,又能代替人自动修改结构参数呢?这一问题的解决萌生了光学自动设计方法。

要利用计算机来自动修正结构参数,找出符合要求的解,关键的问题还是要给出像差与结构之间的函数关系。为了解决这样的棘手问题,工程数学中最常用的一种方法就是将函数表示成自变量的幂级数,根据需要和可能,选到一定的级次,再通过实验或数值计算的方法,得出若干抽样点的函数值,则可以列出足够数量的方程式,求解出幂级数的系数,这样即可确定函数的幂级数形式。

最简单的情形,是只选取幂级数的一次项,即将像差与结构参数之间的函数关系,近似用线性方程式来替代:

式中,f0为初始结构的像差值,(x01,x02,…,x0n)为初始结构的结构参数,f为像差的目标值,…为像差对各个自变量的一阶偏导数。

目前存在的问题是如何得到　?为此,通过差商替代偏导的方法,解决这一问题。具体的方法是,首先计算初始结构的像差值F0,然后将初始结构的某一结构参数改变一微小增量,使x=x0+Δx,重新计算像差值得到F,计算相应的像差增量Δf=f-f0,用像差对该自变量的差商代替微商(偏导)

对每个自变量重复上述计算,可得到各种像差对各个自变量的全部偏导数。利用这些近似的偏导数,像差与结构参数之间的隐晦关系就可以用式(3-2)的线性方程式近似表示。

将这些像差线性方程式全部列出,得到像差和自变量之间的线性方程组:

方程组(3-3)称为像差线性方程组。用它近似代替像差式(3-1),由此,利用计算机进行光学自动设计的想法才具有可实施性。

一般地,为了表达简便,数学上,可以用矩阵表示线性方程组。设

这样像差线性方程组的矩阵形式为