轴外像差的规律性

前面讨论了轴外像差的基本概念,包含子午彗差、子午场曲、弧矢彗差、弧矢场曲、像散、畸变、垂轴色差。仅看像差概念,比较抽象。上述7种轴外像差,除畸变外,都影响成像的清晰度。但造成点像弥散的规律,如果仅讨论其中的一种像差,不便于形成总体印象;为了便于讨论,通常假定其他像差不存在,仅存在某种像差,讨论对点像弥散的影响规律。如将子午彗差与弧矢彗差看成轴外彗差,将子午场曲与弧矢场曲合在一起,讨论其规律。

2.3.3.1　彗差

彗差是光学系统中极其重要的像差,无论视场大小,都要注意控制彗差。

如果系统仅存在彗差,将轴外物点发出的充满入瞳的光线,按照入瞳上围绕光瞳中心分出不同的带区,则经过系统后,主光线周围细光束在像面上交于主光线与像面的交点;主光线周围环带区zone 1的光线在像面上形成一个小圆斑,圆斑中心稍微偏离主光线与像面的交点;主光线周围环带区zone 2的光线在像面上形成一个中等圆斑,圆斑中心与主光线及像面的交点之间偏离变大;主光线周围环带区zone 3的光线在像面上形成一个较大圆斑,圆斑中心与主光线及像面的交点之间偏离更大,如图2-36所示。

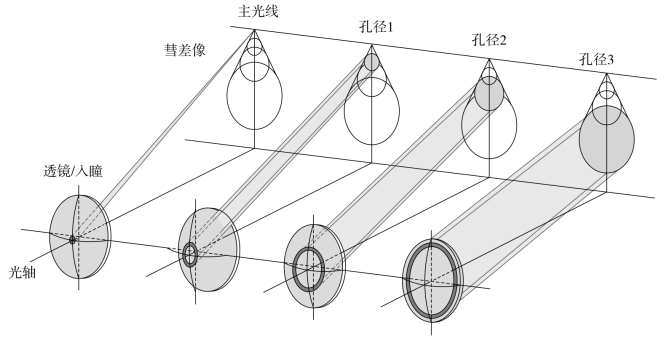
图2-36　存在彗差时不同环带光线在像面上的圆斑移动规律

仔细核对可以发现,每一个环带光线对应不同的光束孔径高度,每一个环带光线在像面上形成的圆斑在竖直(子午面)直径方向,下端点与主光线在像面上的交点之间的距离,就是该孔径带的子午彗差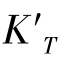;上端点与主光线在像面上的交点之间的距离,就是该孔径带的弧矢彗差。

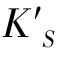因此,随孔径高变化的子午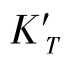彗差、弧矢彗差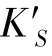,其实是确定了仅存在彗差时该孔径带的弥散圆大小。图2-36展现的弥散斑呈彗星扫尾状的分布,也是该像差称为“彗差” 的形象写照。

计算彗差时,只需追迹一组子午光线对和一组弧矢光线对,如果像方主光线与像面的交点高度为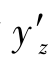,子午光线对与像面的交点高度分别为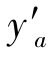,,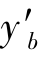弧矢光线对与像面的交点高度相同,为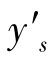,如果系统的场曲不大,则

子午彗差:

弧矢彗差:

彗差是孔径h(或U)和视场ω(或y)的函数。一般函数关系为:

式(2-25)中每一项的物理含义如表2-4所示。

表2-4　彗差与视场、孔径的关系说明

初级彗差情况如下:

(www.xing528.com)

小视场、小相对孔径情况下,使用正弦彗差:

彗差校正的理想结构形式是孔径光阑居中的对称式光学系统结构。

2.3.3.2　场曲与像散

计算场曲与计算彗差一样,需要追迹轴外物点发出的子午线对或弧矢线对,由光线对在像方的数据,求出线对交点偏离高斯像面的轴向距离。

本质上反映场曲性质的量为细光束子午场曲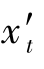和细光束弧矢场曲。

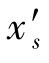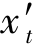和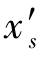的计算仅需用专用公式,追迹一条主光线,仅与视场有关。

当视场较大时,场曲像差表现明显。

场曲与像散这两种像差具有一种伴生现象,必须采用恰当的光学结构形式,如正负光组远离型,才能很好地同时消除像散与场曲。

2.3.3.3　主光线的像差:畸变与垂轴色差

畸变不影响成像清晰度,但影响像的变形,为了让设计者对畸变的量级产生感性认识,这里给出畸变为0、±1%、±2%、±5%、±10%、±20%的网格图像变形效果图,如图2-37所示。可以看出,基于人眼的分辨率,畸变绝对值小于1%的网格图变形,人眼已经看不出变形,这是我们设计光学系统对畸变量允许的经验值。

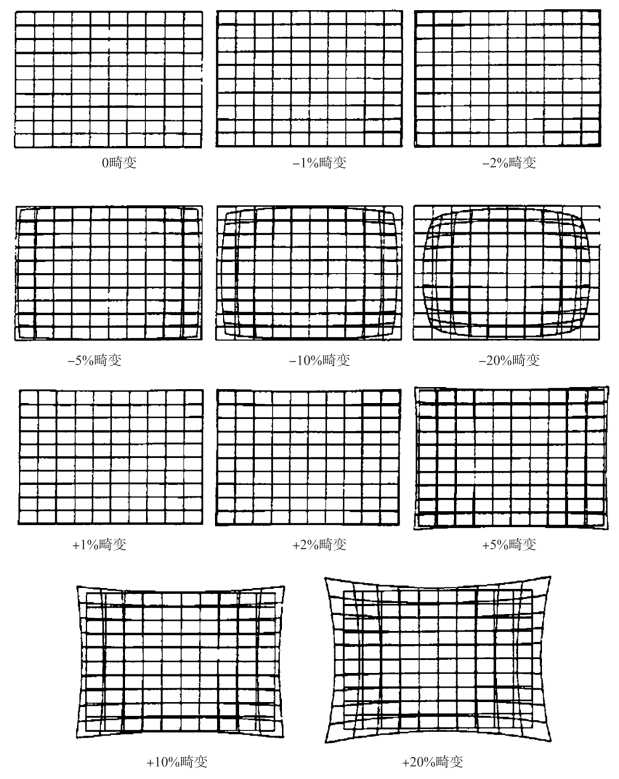
图2-37　不同百分比畸变的变形效果

畸变与视场y(或ω)有关,是视场y(或ω)的奇函数,函数关系为

畸变很难完全消除,只有光阑位于中间,β=-1的对称光学系统,畸变才能被自动校正。

在可见波段,垂轴色差使一个白光像点形成一条由红到紫的短线,影响像面清晰度。随视场y(或ω)大小变化:

式中,线性项为初级垂轴色差;高次项是不同色光的畸变差别所致,是高级垂轴色差,又称色畸变。