轴外物点指具有一定视场的偏离光轴的物点,如物点位于有限远,一般用偏离光轴的垂轴距离表示轴外物点的视场大小;对于位于无限远的物点,其向光学系统发出的光是一束平行光,用平行光与光轴所成的夹角表示轴外物点的视场。
因此,由轴外物点进入共轴系统成像的光束,对于系统光学面来说,是一束斜光束。充满光瞳的入射光束中的每一根光线,不是同时触及光学面。对于共轴旋转对称系统,包含光轴的平面有无限个,但每一个包含光轴的平面具有各向同性。不失一般性,为了方便描述轴外物点的光束结构,通常将轴外物点放在某一个光轴平面与物平面的交线上。
因此可以定义,包含物点和光轴的平面为子午面,包含物点且垂直于子午面的平面为弧矢面。同时,忽略光学系统的光学面等具体结构,保留系统的屈光性能,将任一光学系统简化成物光束、光瞳、像方光束,光瞳是物像方的分界面,如图2-25所示。

图2-25 轴外物点的光束结构
将物点发出,位于子午面内的光线称为子午光线,位于弧矢面内的光线称为弧矢光线。轴外物点发出的物方光束,一般是物点与光瞳面上点的连线,这些光束是顶点位于物点、底面为光瞳面的锥形光束,根据立体几何原理,如将物方光线看作矢量,物方光束中的任意一根光线,都可以用一根子午光线与弧矢光线合成;或者,换句话说,空间任意一根物方光线,都可以分解成相应的子午光线与弧矢光线分量。
除此之外,轴外物点的光线结构,还有一根重要的光线,它既属于子午面,又属于弧矢面,是轴外光束的中心光线,即子午面与弧矢面的交线,我们称之为主光线。
如果物点沿垂直于光轴的线段靠近或远离光轴,则物方轴外线视场在变小或变大,主光线靠近光轴或远离光轴,子午面没有变化,只是轴外物点发出的子午成像光束在子午面内的位置在改变;但弧矢面随着物点位置的变化而变化。
因此,讨论轴外物点的像差,可以进一步将轴外物点的光束结构简化成子午光线、弧矢光线、主光线。然后,跟轴上点像差思路一样,考察子午光线、弧矢光线经过系统后围绕轴外中心线——主光线的对称性、光线像点与目标像点之间的偏离等典型特征变化情况,来定义轴外物点的像差,并研究其变化规律与控制方法。
2.3.2.1 子午像差
以有限远轴外物点为例,我们考察像方子午光束相对于主光线、子午像点相对于目标像点的偏离与否。不失一般性,假设轴外物点位于光轴下方,为了考察轴外子午光线相对于主光线的偏离大小,通常选取子午光线对,即在子午面内,让物点发出一对孔径角大小相等、符号相反的上下光线。
我们知道,轴上物点发出的上下线对,以光轴为对称,且同时到达光学面。轴外物点与之不同,虽然子午光线对相对于主光线对称,但子午线对的上光线、下光线不是同时达到光学面,其含义是轴外物方子午光线对在触及光学面的时刻有先后,这种情况带来的可能后果,是像方的子午线对通常不再对称于主光线,如图2-26所示。

图2-26 子午面的光束结构
图2-26中,轴外物点B点发出的子午线对:上光线BM+与下光线BM-,在物方对称于主光线BP,即BP是BM+和BM-的中心光线。物AB在像方的理想像为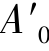
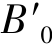 ,主光线BP在理想像面上的交点为
,主光线BP在理想像面上的交点为 ,子午线对BM+和BM-在像方的交点为
,子午线对BM+和BM-在像方的交点为 。如果系统结构没有被精心设计,子午线对BM+和BM-的像点不在像方主光线上,即在像方线对不再以主光线为中心光线,则出现线对失对称的像差,这种失对称现象,会造成像点向一个方向弥散,我们称其为彗差。其定义为,像方子午线对交点
。如果系统结构没有被精心设计,子午线对BM+和BM-的像点不在像方主光线上,即在像方线对不再以主光线为中心光线,则出现线对失对称的像差,这种失对称现象,会造成像点向一个方向弥散,我们称其为彗差。其定义为,像方子午线对交点 离开主光线的垂直距离,用符号
离开主光线的垂直距离,用符号 表示,下标T表示子午面的像差,交点
表示,下标T表示子午面的像差,交点 在主光线下方,彗差符号为负,相反为正。
在主光线下方,彗差符号为负,相反为正。
如果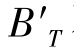 不在系统像面上,则其离开像面的轴向距离,也是造成像面上像点弥散的一种像差,由于这种像差会破坏平面像的状态,造成像平面的弯曲,我们称之为场曲,在图2-26中,以符号
不在系统像面上,则其离开像面的轴向距离,也是造成像面上像点弥散的一种像差,由于这种像差会破坏平面像的状态,造成像平面的弯曲,我们称之为场曲,在图2-26中,以符号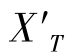 表示。之所以用“X”表示场曲,因为过去的系统坐标系,习惯以X轴为光轴,场曲沿光轴方向度量。虽然,现在常用Z轴来定义光轴,但场曲的符号已经用习惯了,成为约定俗成的符号,因此,本书中仍以
表示。之所以用“X”表示场曲,因为过去的系统坐标系,习惯以X轴为光轴,场曲沿光轴方向度量。虽然,现在常用Z轴来定义光轴,但场曲的符号已经用习惯了,成为约定俗成的符号,因此,本书中仍以 表示子午场曲,后面弧矢面采用符号情况与之相同。场曲
表示子午场曲,后面弧矢面采用符号情况与之相同。场曲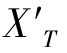 的计算零位为目标像面(图2-26中取了理想像面),
的计算零位为目标像面(图2-26中取了理想像面), 在像面的左边,符号为负,否则相反。
在像面的左边,符号为负,否则相反。
图2-26中,轴外物点B代表了视场的大小,子午线对BM+和BM-代表了光线孔径的大小,因此子午彗差 和子午场曲
和子午场曲 既与视场有关,又与孔径有关。以单透镜为例,在ZEMAX软件上,通过光线追迹展现子午彗差
既与视场有关,又与孔径有关。以单透镜为例,在ZEMAX软件上,通过光线追迹展现子午彗差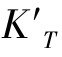 和子午场曲
和子午场曲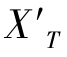 随视场与孔径的变化规律,分别如图2-27和图2-28所示。
随视场与孔径的变化规律,分别如图2-27和图2-28所示。
图2-27反映了子午彗差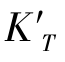 和子午场曲
和子午场曲 在同一孔径情况下随视场的变化规律。可以得出结论:随着物高(视场)的增大,子午光线的不对称性增大,子午彗差与子午场曲不断增大;当视场变为正视场时,子午彗差与子午场曲绝对值不变,子午彗差变号,子午场曲不变号,子午彗差是视场的奇函数,子午场曲是视场的偶函数。
在同一孔径情况下随视场的变化规律。可以得出结论:随着物高(视场)的增大,子午光线的不对称性增大,子午彗差与子午场曲不断增大;当视场变为正视场时,子午彗差与子午场曲绝对值不变,子午彗差变号,子午场曲不变号,子午彗差是视场的奇函数,子午场曲是视场的偶函数。

图2-27 子午彗差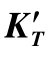 和子午场曲
和子午场曲 随视场的变化规律
随视场的变化规律

图2-28 子午彗差 和子午场曲
和子午场曲 随孔径的变化规律
随孔径的变化规律
图2-28反映了子午彗差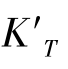 和子午场曲
和子午场曲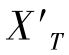 在视场(物高)不变的情况下随光束孔径的变化规律,光束孔径分别取全孔径、0.707h、0.5h、0.3h。由图2-28,可以得出结论:
在视场(物高)不变的情况下随光束孔径的变化规律,光束孔径分别取全孔径、0.707h、0.5h、0.3h。由图2-28,可以得出结论:
(1)子午彗差随光束孔径减小,迅速减到0。
(2)子午场曲随孔径减小,最终不一定为0,而为定值,称之为细光束子午场曲。在图2-26中,当光束孔径减小到0时,子午线对的像点 逐渐移到主光线上,变成
逐渐移到主光线上,变成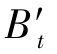 ,但
,但 与主光线及像面的交点
与主光线及像面的交点 不重合,
不重合,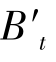 到像面的轴向距离,定义为细光束场曲
到像面的轴向距离,定义为细光束场曲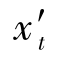 ;子午细光束焦点
;子午细光束焦点 的具体位置,基于轴外近轴光线的三角关系,可以推导出计算式。为了体现区别,可以称
的具体位置,基于轴外近轴光线的三角关系,可以推导出计算式。为了体现区别,可以称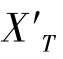 为宽光束子午场曲,称
为宽光束子午场曲,称 为细光束子午场曲。
为细光束子午场曲。
显然,细光束子午场曲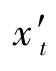 仅与视场有关;宽光束子午场曲
仅与视场有关;宽光束子午场曲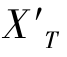 既与视场有关,也与孔径有关。为了使问题简化,我们采取分离变量法,设
既与视场有关,也与孔径有关。为了使问题简化,我们采取分离变量法,设 (h,y)=
(h,y)= (h)+
(h)+ (y),其中
(y),其中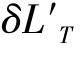 (h)可以称为子午球差,其与轴上点的球差具有相关性,可以采取轴上点球差校正的结构与方法来控制轴外点的球差。这样,如果我们知道了球差和细光束场曲的一般校正办法,宽光束子午场曲的校正问题就迎刃而解了。
(h)可以称为子午球差,其与轴上点的球差具有相关性,可以采取轴上点球差校正的结构与方法来控制轴外点的球差。这样,如果我们知道了球差和细光束场曲的一般校正办法,宽光束子午场曲的校正问题就迎刃而解了。
2.3.2.2 弧矢像差
同样,对于弧矢面光束,我们也取弧矢光线对。弧矢光线对与子午光线对的不同之处,表现在弧矢线对以主光线对称,同时触及光学面,表明弧矢光线对在物像方始终以子午面对称,其线对交点相对于子午面的对称性没有被破坏,因此弧矢线对的交点一定在子午面上。弧矢光线对与子午光线对的共同之处,表现在轴外弧矢线对也是斜光束入射光学面,这样弧矢线对的交点不一定在主光线上,图2-29给出了弧矢面的光束结构。
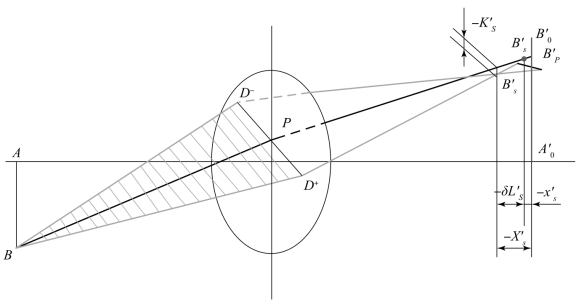
图2-29 弧矢面的光束结构
图2-29中,AB是物平面,B点为轴外物点,P点为轴外视场的光瞳中心,BP是物方主光线,平面BD+D-为轴外物点B的弧矢面,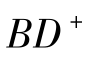 和BD-为对主光线BP具有相同孔径角的弧矢光线对。与图2-26相同,物AB在像方的理想像为
和BD-为对主光线BP具有相同孔径角的弧矢光线对。与图2-26相同,物AB在像方的理想像为
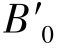 ,主光线BP在理想像面上的交点为
,主光线BP在理想像面上的交点为 。弧矢光线对在像方的交点为
。弧矢光线对在像方的交点为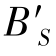 ,由于轴外物点弧矢光线对的斜光束特性,
,由于轴外物点弧矢光线对的斜光束特性, 不一定位于像方主光线
不一定位于像方主光线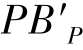 上,也不一定与主光线在像面上的交点
上,也不一定与主光线在像面上的交点 重合,如此也将造成轴外物点B的像点弥散,存在弧矢彗差。
重合,如此也将造成轴外物点B的像点弥散,存在弧矢彗差。
类似于子午面像差,弧矢线对在像方交点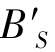 离开主光线的垂轴距离,定义为弧矢彗差,用符号
离开主光线的垂轴距离,定义为弧矢彗差,用符号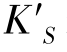 表示,符号规则同子午彗差。
表示,符号规则同子午彗差。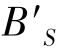 与目标像面(一般为理想像面)之间的轴向距离,定义为弧矢场曲,用符号
与目标像面(一般为理想像面)之间的轴向距离,定义为弧矢场曲,用符号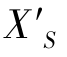 表示。
表示。
弧矢彗差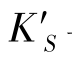 与弧矢场曲
与弧矢场曲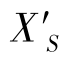 都是既与视场有关,又与孔径有关。与子午像差一样,关于弧矢像差,也具有以下结论:(https://www.xing528.com)
都是既与视场有关,又与孔径有关。与子午像差一样,关于弧矢像差,也具有以下结论:(https://www.xing528.com)
(1)在弧矢光线对孔径高不变时,随着物高(视场)的增大,弧矢光线对偏离主光线的不对称性增大,弧矢彗差与弧矢场曲不断增大;当视场变为正视场时,弧矢彗差与弧矢场曲绝对值不变,弧矢彗差变号,弧矢场曲不变号,弧矢彗差是视场的奇函数,弧矢场曲是视场的偶函数。
(2)弧矢彗差随光束孔径减小,迅速减到0;弧矢场曲随孔径减小,最终不一定为0,而为定值,称之为细光束弧矢场曲。在图2-29中,当光束孔径减小到0时,弧矢线对的像点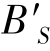 逐渐移到主光线上,变成
逐渐移到主光线上,变成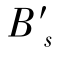 ,但
,但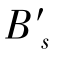 与主光线与像面的交点
与主光线与像面的交点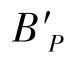 不重合,
不重合,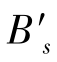 到像面的轴向距离定义为细光束场曲
到像面的轴向距离定义为细光束场曲 。
。
同样,细光束弧矢场曲 仅与视场有关;宽光束弧矢场曲
仅与视场有关;宽光束弧矢场曲 既与视场有关,也与孔径有关。为了使问题简化,设
既与视场有关,也与孔径有关。为了使问题简化,设 (h,y)=
(h,y)=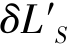 (h)+
(h)+ (y),其中的
(y),其中的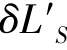 (h)可以称为弧矢球差。
(h)可以称为弧矢球差。 (h,y)与
(h,y)与 (h,y)之间的差别,应该由
(h,y)之间的差别,应该由 (y)与
(y)与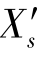 (y)之间的差别决定,
(y)之间的差别决定, (h)、δL′S(h)随孔径h变化的规律是一致的,都与轴上点的球差具有相关性。
(h)、δL′S(h)随孔径h变化的规律是一致的,都与轴上点的球差具有相关性。
 (y)与
(y)与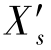 (y)之间的差别,反映了同一物点的子午面与弧矢面之间光线对像差的差别,如果
(y)之间的差别,反映了同一物点的子午面与弧矢面之间光线对像差的差别,如果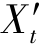 (y)与
(y)与 (y)量值不同,则表明子午面与弧矢面光束结构之间的不一致性;或者说,子午光束与弧矢光束之间失去了对称性。此时的光束结构如图2-30所示,子午细光束与弧矢细光束在像方存在不同的焦点,追迹主光线周围包含子午面、弧矢面在内的锥面光束,则细光束子午焦点演变成位于弧矢面内的子午焦线,细光束弧矢焦点演变成位于子午面内的弧矢焦线。子午面与弧矢面细光束焦点之间的不一致性,也将造成像点的弥散,定义这种不一致性偏差
(y)量值不同,则表明子午面与弧矢面光束结构之间的不一致性;或者说,子午光束与弧矢光束之间失去了对称性。此时的光束结构如图2-30所示,子午细光束与弧矢细光束在像方存在不同的焦点,追迹主光线周围包含子午面、弧矢面在内的锥面光束,则细光束子午焦点演变成位于弧矢面内的子午焦线,细光束弧矢焦点演变成位于子午面内的弧矢焦线。子午面与弧矢面细光束焦点之间的不一致性,也将造成像点的弥散,定义这种不一致性偏差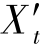 -
- =
= 为像散。
为像散。

图2-30 像散像差的光束结构
存在像散 时,也表明同一物平面,子午面细光束所成的像是弯曲的曲面T′;弧矢细光束所成的像,不是同一曲面T′,而是另一曲面S′,如图2-31所示。
时,也表明同一物平面,子午面细光束所成的像是弯曲的曲面T′;弧矢细光束所成的像,不是同一曲面T′,而是另一曲面S′,如图2-31所示。
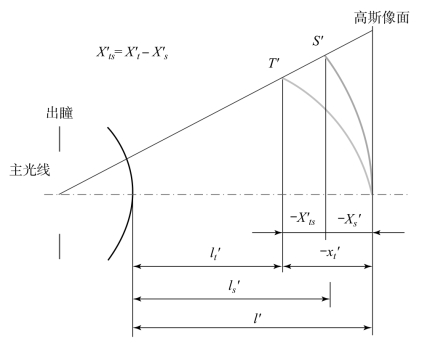
图2-31 存在像散时子午面与弧矢面细光束出现不同的弯曲像面
2.3.2.3 主光线的像差
1.畸变
对于轴外物点的单色像差而言,如果轴外物点不存在子午像差和弧矢像差,则轴外物点可以成清晰的像。轴外物点发出的球面波经过系统后,像方的出射波面仍然为球面波,球面波的球心为主光线与像平面交点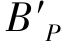 ,半径为系统出瞳中心与
,半径为系统出瞳中心与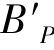 连线。
连线。
用于测量或观瞄领域的光学系统,要求系统成像清晰且不变形。然而,如果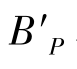 不与理想像点
不与理想像点 重合,或者轴外像点的垂轴放大率随视场大小变化,则轴外像点产生变形,变形大小用
重合,或者轴外像点的垂轴放大率随视场大小变化,则轴外像点产生变形,变形大小用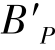 与
与 之间的垂轴距离表示,如图2-32所示。
之间的垂轴距离表示,如图2-32所示。

图2-32 主光线像高与理想像高的偏差
图2-32中,以单透镜示意透镜成像系统,p点为入瞳中心,Bp为轴外物点B的主光线,p′为p的理想像点,也是B点的理想像点 像方光线的反向延长线与光轴的交点;P″为p的实际像点,也是主光线Bp在像方与像面交于
像方光线的反向延长线与光轴的交点;P″为p的实际像点,也是主光线Bp在像方与像面交于 点的像方光线的反向延长线与光轴的交点。理想像点
点的像方光线的反向延长线与光轴的交点。理想像点 对应的像高为
对应的像高为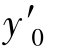 ,主光线与像面交点
,主光线与像面交点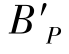 的像高为
的像高为 ,则轴外像点的变形量由式(2-20)表示:
,则轴外像点的变形量由式(2-20)表示:
![]()
式(2-20)给出的长度量绝对值,不利于使用者产生感官体验,进行畸变影响量的评价。光学系统中,常用百分畸变q′表示:
![]()
对fθ透镜,物体在无限远,物方视场角为θ,ZEMAX中将理想像高取为 =f′θ。
=f′θ。
存在畸变时,本质上是垂轴放大率随视场由小到大变化,不再是一常数,使网格状的平面成像变形,如图2-33所示。如β(y)>β0,为枕形畸变;β(y)<β0,则为桶形畸变。
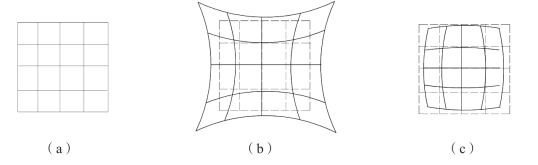
图2-33 畸变的正负与变形状况
(a)没有畸变;(b)枕形畸变;(c)桶形畸变
2.垂轴色差
对于透射系统,无论对轴上物点还是轴外物点都会产生色差,而且每一根光线都因色差产生与中间波长光线的偏离。为了抓住问题本质,对色差展开讨论,我们分成随光束孔径高变化的色差和随视场变化的色差。其中随光束孔径高变化的色差,轴外物点与轴上物点规律相同、差别不大,由轴向色差![]() 表示;随视场变化的色差,由随视场变化的主光线经过系统后的色散大小来表示,如图2-34所示。
表示;随视场变化的色差,由随视场变化的主光线经过系统后的色散大小来表示,如图2-34所示。
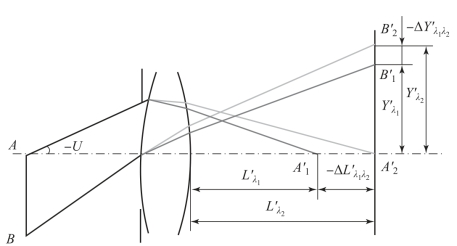
图2-34 主光线的垂轴色差
图2-34中,A为轴上物点,其发出孔径角为U的轴上光线,经过系统后,对应的轴向色差为![]() ;B为轴外物点,主光线经过系统后,波长λ1的主光线与像面(一般为中间波长的像面)的交点
;B为轴外物点,主光线经过系统后,波长λ1的主光线与像面(一般为中间波长的像面)的交点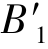 的高度为
的高度为![]() ,波长λ2的主光线与像面的交点
,波长λ2的主光线与像面的交点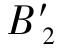 的高度为
的高度为![]() ,则
,则
 之间的垂轴高度差,定义为垂轴色差,即
之间的垂轴高度差,定义为垂轴色差,即
![]()
如果工作波段为可见波段,则λ1为F光波长,λ2为C光波长,垂轴色差![]() ,如图2-35所示。
,如图2-35所示。

图2-35 可见波段的垂轴色差
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




