采用加权抛物线拟合法求解分度环面螺旋线上的点

采用曲面造型的方法测量实际螺旋线上的点，即关闭测头测量半径补偿，测量包含被测量点的实际螺旋面上的一个面片，测量得到的是该面片的等距曲面，再反求实际曲面，并在实际曲面上找到分度环面上的点，即为分度环面实际螺旋线上的点。

为了方便地反求实际曲面螺旋线上的点，采用边界曲线是加权抛物线的Coons曲面DEM模型^[36]，以螺旋线上被测点对应测头球心的（x，y）为中心在平面xOy内取7×7=49个网格点（如图10-9所示与x轴和y轴平行的线的交叉点），网格线纵横向间距都为d=0.5mm。拟合出经过中间5×5=25个网格点（见图10-9中所示圆圈点）在xOz和yOz两个平面内的加权抛物线方程及其切线，由经过每个网格点的两条切线可以得到拟合螺旋面的法线，求此拟合螺旋面的等距曲面即实际螺旋面，进而求得分度环面螺旋线上的点。边界曲线是加权抛物线的Coons曲面的模型^[36]，如图10-10所示。

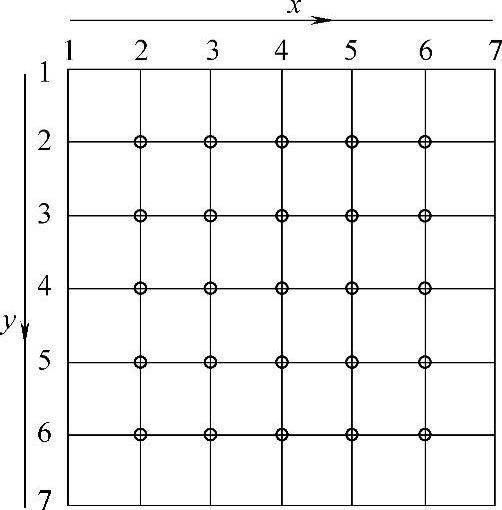
图10-9 包含测量点的面片上等距网格点示意图

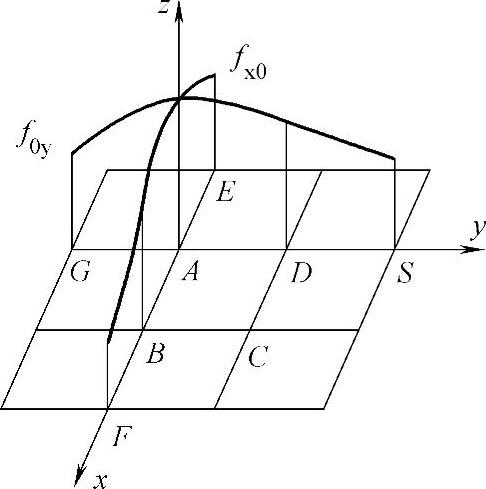
图10-10 边界曲线是加权抛物线的Coons曲面的模型

在图10-10中，坐标原点在点A，那么曲面上对应点A两条边界曲线的加权抛物线方程分别为

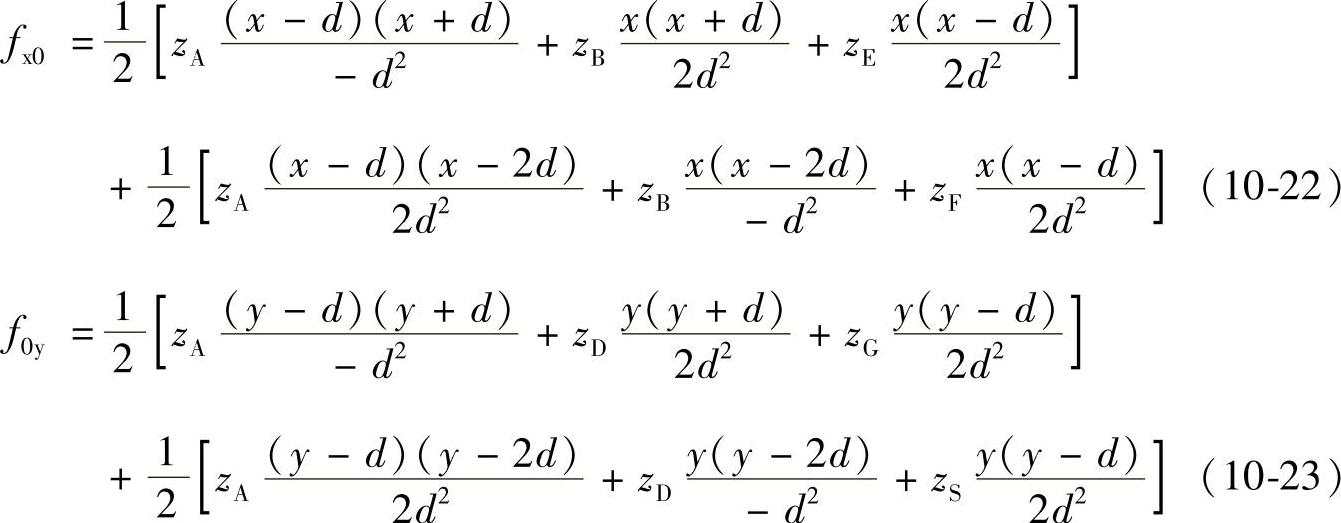
式（10-22）和式（10-23）分别对x和y求导，得两曲线f_x0和f_0y的切线方程为(www.xing528.com)

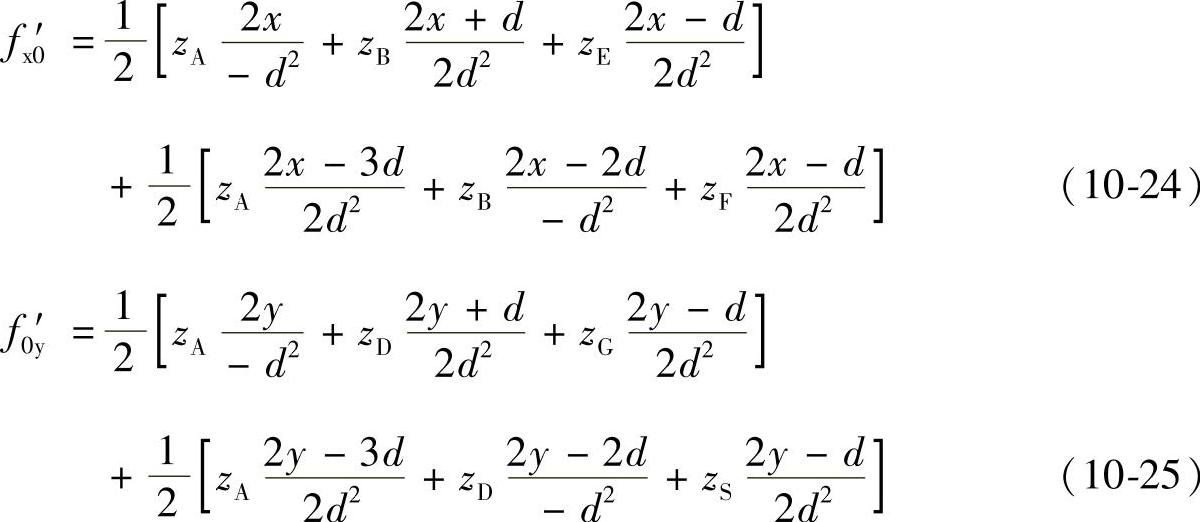
1）将x=0和x=d分别代入式（10-24），得到点A和点B对应曲线f_x0的切线f′_x0的z坐标为

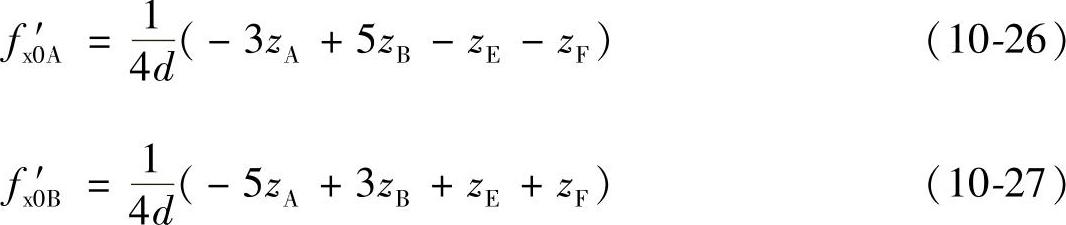
2）将y=0和y=d分别代入式（10-25），得到点A和点D对应曲线f_y0的切线f′_y0的z坐标为

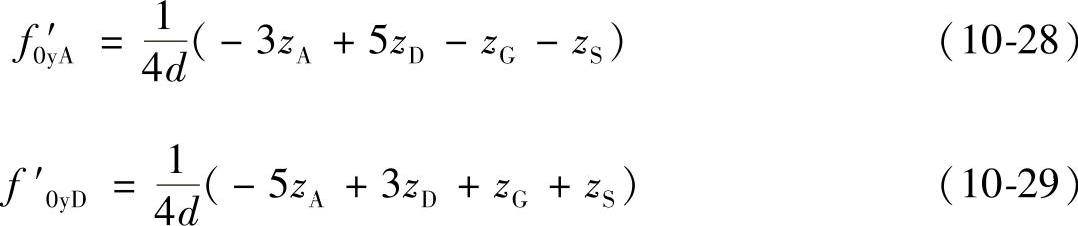
将格点对应的曲面上点的两个切矢量相乘，可以得到曲面点的法矢量。

因此，可计算包含测量点的面片上等距5×5=25个网格点（如图10-9中圆圈所示）。沿x方向，从点2到点5，可以计算每个点对应的曲面曲线的切矢量f′_x0，注意：每次计算时，坐标原点移至计算点。再计算点6对应的曲面曲线的切矢量f′_x0；沿y方向，从点2到点5，可以计算每个点对应的曲面曲线的切矢量f′_0y，注意：每次计算时，坐标原点移至计算点。再计算点6对应的曲面曲线的切矢量f′_0y。

计算从点2到6对应曲面的法矢量。根据球头半径r，可求等距曲面（即蜗杆右侧螺旋面）上的对应点，由这些点组成蜗杆右侧螺旋面包含测量点的一小块。在此小块齿面上，给定一个x值，根据在分度环面上和在该齿面上，可以求得分度环面螺旋线上一个点。