研究螺旋参数和蜗杆头数对蜗杆副接触质量的影响

在双自由度直线标准环面蜗杆副中，以a=250mm、i₁₂=40、z₁=1、z₂=40、d₁=90mm、d_b=160mm为实例（蜗杆传动的几何参数和尺寸计算见表8-1中算例1）研究直线刀刃运动的螺旋参数p_d和蜗杆头数对蜗杆根切、边齿顶厚度、蜗杆双线接触区和蜗轮二次接触区的蜗杆啮合长度以及蜗轮齿面接触区分布等接触质量的影响。在下面讨论中，为便于比较，取中心距a、蜗杆分度圆直径d₁、蜗轮分度圆直径d₂、基圆直径d_b不变化，蜗杆头数变化，即取z₁=2、3、4、5和6时，蜗轮齿数不变，即z₂=40。

1.螺旋参数p_d和蜗杆头数z₁对蜗杆根切的影响研究

由式（6-79），即由式（6-60）、式（6-63）和式（6-78），可解蜗杆螺旋面Σ₁上的曲率干涉界线，检验蜗杆螺旋面是否根切。

三个未知数u、δ和φ，给定一个展成蜗杆转角φ值和刀刃附加转角δ的初值，由式（6-60）求得u值，再由式（6-78）迭代求解δ的终值，从而得到曲线Ψ_d上的一个点；改变φ值，逐点求解可得到Σ₁上展成蜗杆曲率干涉界线Ψ_d。

蜗杆副其他参数不变，只改变蜗杆头数z₁和C_p，C_p取-1.5、-1.0、-0.5、0、0.5、1.0、1.5、2.0、2.5、3.0、3.5，计算并比较展成蜗杆的曲率干涉界线Ψ_d在蜗杆轴截面上的位置变化。注意与p_d有关的量：i₁₂和C_p变化，但a、z₂、d₁、d₂、m_t和h_f1不变。

图8-11为不同蜗杆头数和不同C_p时展成蜗杆的曲率干涉界线Ψ_d在蜗杆轴截面上的位置图，其中图8-11a、b、c、d、e和f分别为z₁=1、2、3、4、5、6时、C_p取-1.5、-1.0、-0.5、0、0.5、1.0、1.5、2.0、2.5、3.0、3.5时展成蜗杆的曲率干涉界线Ψ_d在蜗杆轴截面上的位置图。

1）C_p越大，根切界线越靠近蜗杆轴线、越接近直线、越平行于蜗杆轴线。随着C_p减小，根切界线从蜗杆齿根圆弧内向蜗杆螺旋面移动，在啮入端移动得更快更接近蜗杆螺旋面，根切的危险性大。

2）当z₁较小时，根切界线在啮出端密集，在啮入端较稀疏。随着z₁的增大，根切界线在啮出端变得稀疏。

表8-3为蜗杆头数z₁与蜗杆不根切的系数C_p最小值和p_d最大值对照表，图8-12为蜗杆头数z₁与蜗杆不根切的系数C_p最小值的关系曲线图。

表8 - 3 蜗杆头数z₁与蜗杆不根切的系数C_p最小值和p_d最大值对照表

2.螺旋参数p_d和蜗杆头数对蜗杆边齿顶厚度的影响研究

蜗杆副其他参数不变，只改变蜗杆头数z₁和C_p，z₁取1、2、3、4、5，按边齿顶厚s_b1=k_sm_t=3.59mm即可计算最大的C_p值和最小的p_d值，计算中没有降低环面蜗杆边齿顶高，即式（8-44）中e=0。表8-4为蜗杆头数z₁与蜗杆边齿顶不变尖的系数C_p最大值和p_d最小值对照表，图8-13为蜗杆头数z₁与蜗杆边齿顶不变尖的最小p_d值关系曲线图。

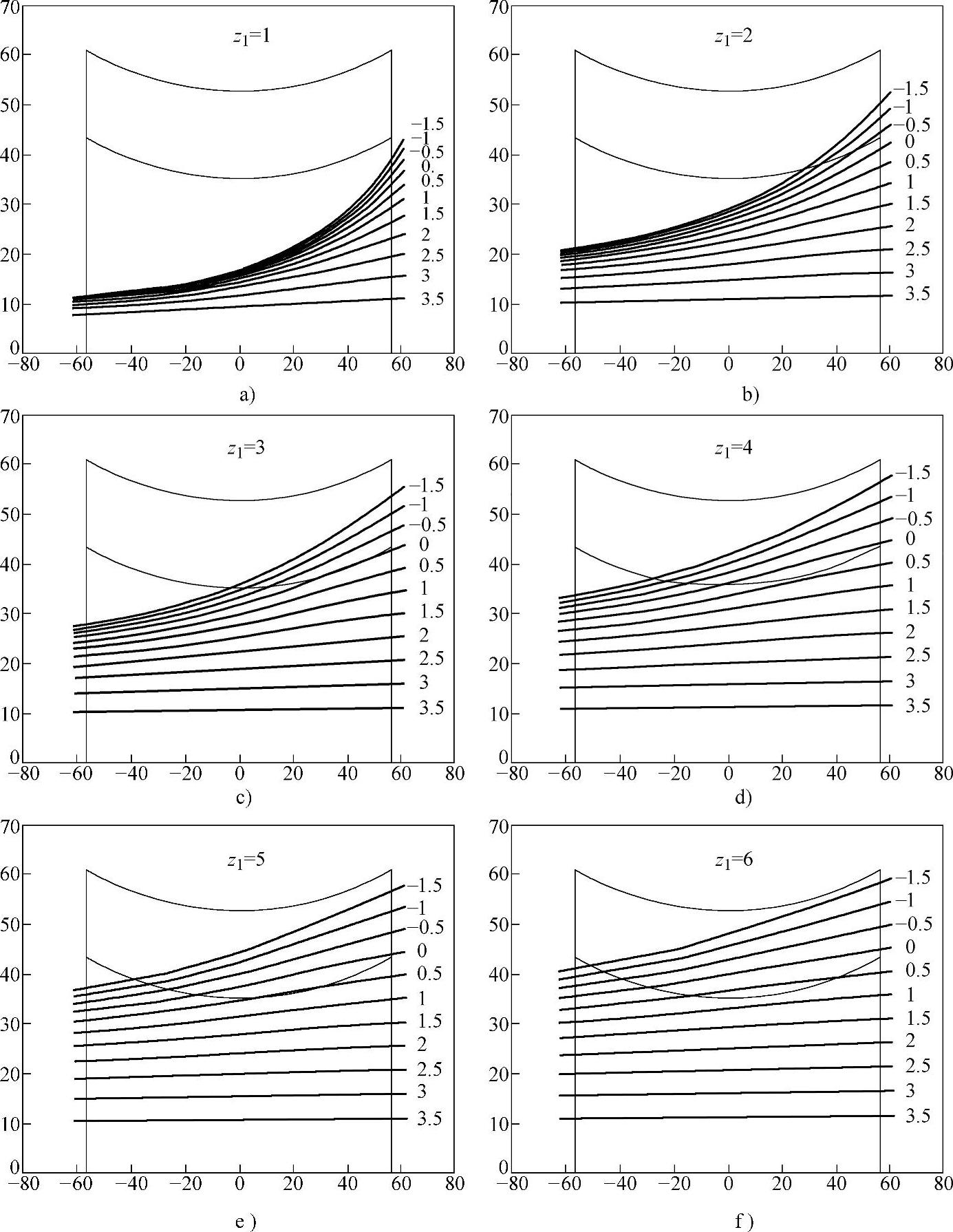
图8-11 不同蜗杆头数和C_p时展成蜗杆的曲率干涉界线Ψ_d在蜗杆轴截面上的位置图

如果式（8-44）中e＞0，可以提高表8-4和图8-13中的C_p最大值（减小p_d最小值）。从表8-3和表8-4可看出，当z₁＞3时，需要取e＞0，降低边齿顶高，切去齿顶变尖部分。

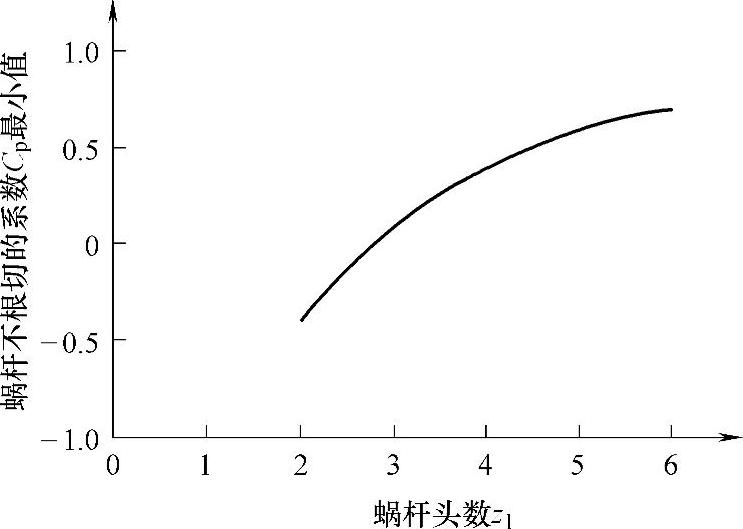
图8-12 蜗杆头数z₁与蜗杆不根切的系数C_p最小值的关系曲线图

表8 - 4 蜗杆头数z₁与蜗杆边齿顶不变尖的系数C_p最大值和p_d最小值对照表

3.螺旋参数p_d和蜗杆头数对蜗轮二次接触区蜗杆啮合长度的影响研究

由第7章知：对于标准传动（i_d1=i₂₁、a_d=a），蜗轮齿面Σ₂上的原接触区Σ_2A和新接触区Σ_2B的切线是蜗轮齿面Σ₂上瞬时接触线奇点轨迹曲线，简称曲线N。N曲线在蜗杆螺旋面Σ₁上的共轭曲线是Σ₁的啮合界线Φ_φ1。N曲线与虚拟产形面Σ_d啮合界线Φ_dφ重合。

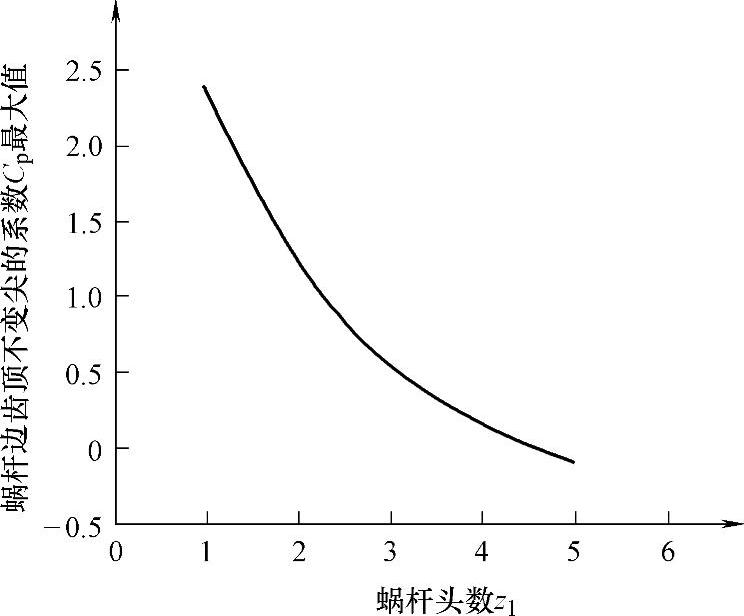
图8-13 蜗杆头数z₁与蜗杆边齿顶不变尖的系数C_p最大值的关系曲线图

N曲线在蜗杆轴向把蜗杆分成两部分，从N曲线到蜗杆啮出端对应蜗轮齿面的二次接触区蜗杆啮合长度，从N曲线到蜗杆啮入端对应蜗轮的一次接触区，一次接触区又分为原接触区和新接触区。原接触区内的二次接触区狭窄，蜗轮齿面不仅接触频率高一倍，而且诱导曲率半径系数很小，容易点蚀，是蜗轮齿面上的薄弱环节。因此，二次接触区越小越好，计算N曲线到蜗杆啮出端的长度可以衡量蜗轮齿面二次接触区的持续时间。为了具有可比性，计算蜗轮二次接触区蜗杆啮合长度l_er与蜗杆工作长度L_w的比值，即蜗轮二次接触区蜗杆啮合长度系数k_er。

式（6-72）为虚拟产形面Σ_d上的啮合界线，它由式（6-30）、式（6-60）和式（6-71）组成。给定一个φ（或者δ）时，由式（6-60）和式（6-71）合解出相应的δ（或者φ）以及u值，由式（6-30）得到虚拟产形面Σ_d上的啮合界线上一点，再由式（6-61）得到σ₀₁里蜗杆螺旋面上啮合界线Φ_φ1的对应点。由图8-5知，从点E比从点F计算的蜗轮二次接触区的蜗杆啮合长度大，所以，从点E计算蜗轮二次接触区蜗杆啮合长度。

由式（8-4）可迭代出点E处的φ（或δ）值，从而得到点E在蜗杆轴向的位置z_01E。那么，蜗轮二次接触区蜗杆啮合长度l_er和蜗轮二次接触区蜗杆啮合长度系数k_er分别为

蜗杆副其他参数不变，只改变蜗杆头数z₁和C_p，C_p取0、0.5、1.0、1.5、2.0、2.5、3.0、3.5，计算并比较蜗杆齿面上蜗杆啮合界线Φ_φ1在蜗杆轴截面上的位置变化。

图8-14为不同蜗杆头数和不同C_p时蜗杆啮合界线Φ_φ1在蜗杆轴截面上的位置图（只显示N曲线从蜗杆齿顶即点F到蜗杆根部点E的部分），其中图8-14a、b、c、d、e和f分别为z₁=1、2、3、4、5、6时、C_p取0、0.5、1.0、1.5、2.0、2.5、3.0时蜗杆啮合界线Φ_φ1在蜗杆轴截面上的位置图。

表8-5为蜗杆头数z₁和C_p与蜗轮二次接触区蜗杆啮合长度l_er和蜗轮二次接触区蜗杆啮合长度系数k_er对照表，图8-15为不同蜗杆头数z₁时p_d与蜗轮二次接触区蜗杆啮合长度系数k_er的关系曲线图。

表8 - 5 蜗杆头数z₁和C_p与蜗轮二次接触区蜗杆啮合长度l_er和蜗轮二次接触区蜗杆啮合长度系数k_er对照表

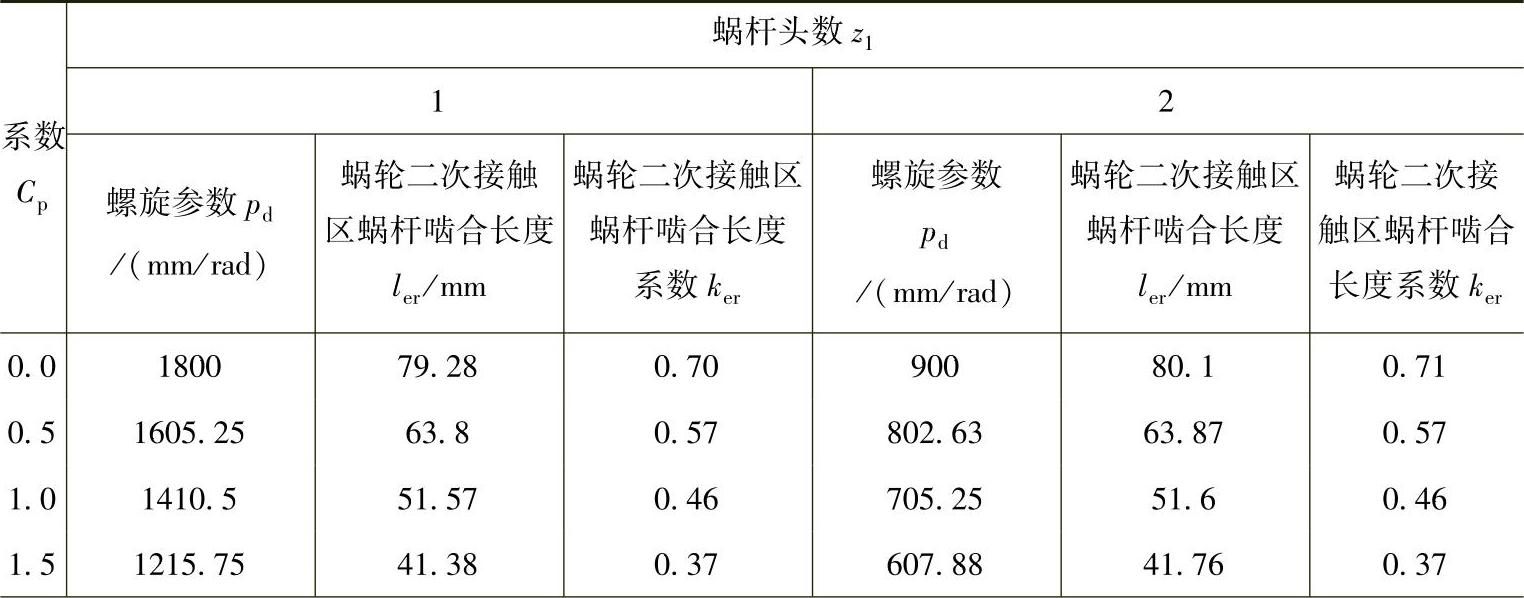
（续）

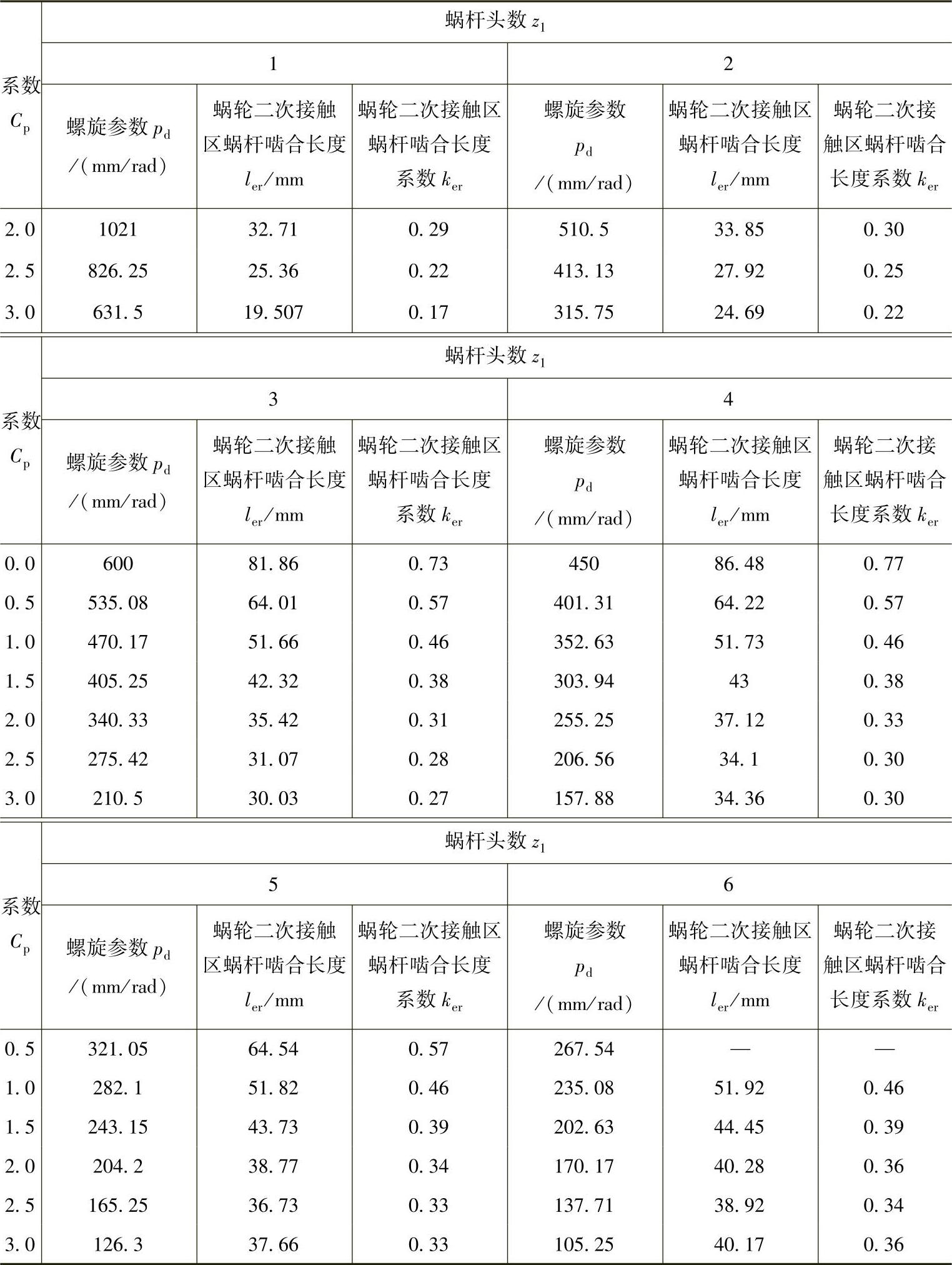
由表8-5和图8-15可以看出，C_p增大时，蜗轮二次接触区蜗杆啮合长度系数减小；蜗杆头数增大时，蜗轮二次接触区蜗杆啮合长度系数减小的幅度变小；在C_p=0.5～1.5时，不同蜗杆头数对应的蜗轮二次接触区蜗杆啮合长度系数差别很小。

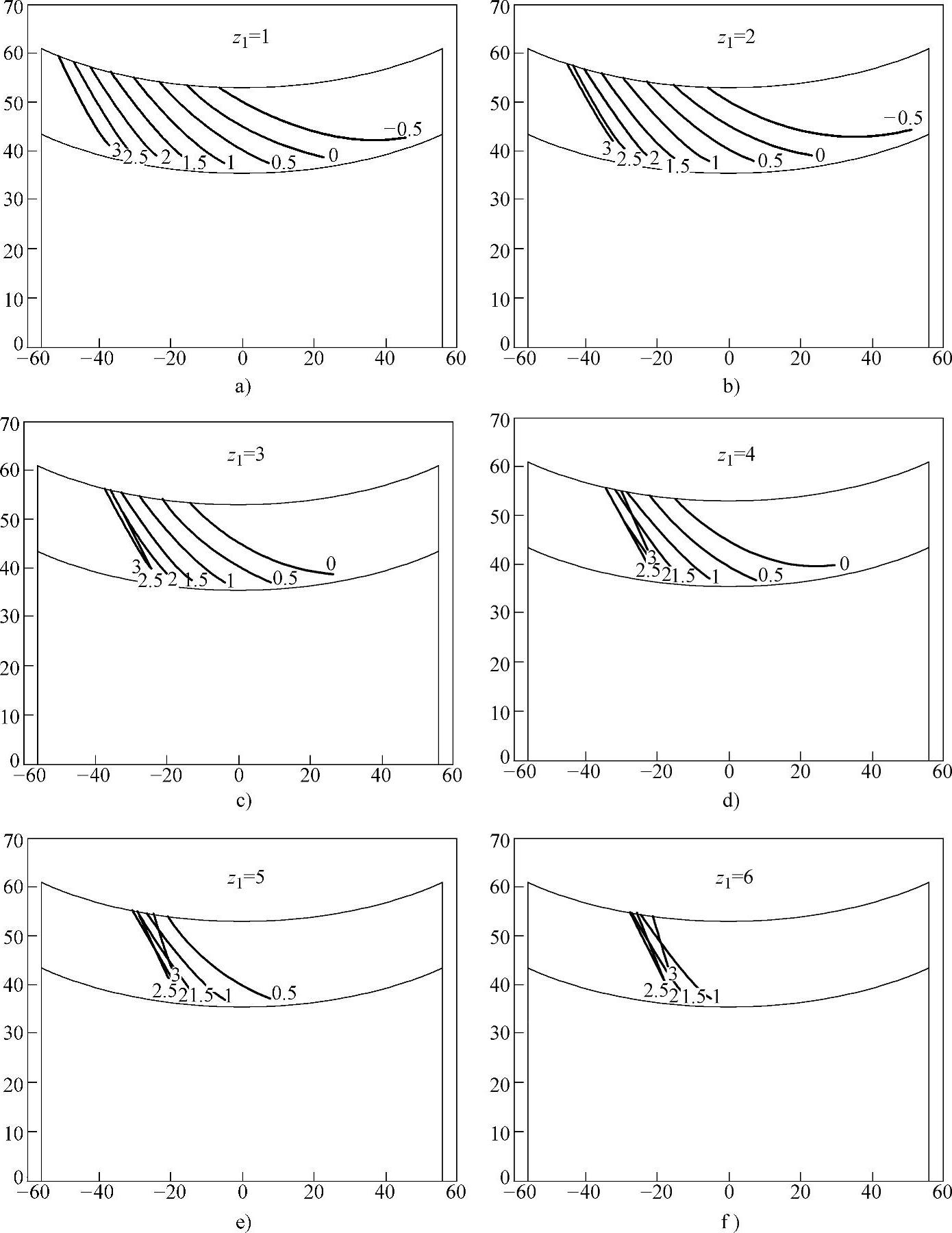
图8-14 不同蜗杆头数和C_p时蜗杆啮合界线Φ_φ1在蜗杆轴截面上的位置图

4.螺旋参数p_d和蜗杆头数对蜗杆双线接触区和蜗轮齿面接触区的影响研究

由式（7-58），给定φ₁值，在蜗轮齿面Σ₂上求瞬时接触线族{Γ₂}。对每一个给定的φ₁值，得到两条瞬时接触线，如图8-5所示（图示为算例1中取C_p=2.0即p_d=1021mm/rad）：1和1′、2和2′、3和3′、4和4′分别为对应不同蜗杆转角φ₁时蜗轮齿面Σ₂上的两条瞬时接触线；1、2、3、4为蜗杆螺旋面Σ₁一次接触线，在蜗轮齿面上N线右边接触区Σ_2A内，Σ_2A是加工蜗杆的产形面Σ_d的一部分再现，称之为原接触区；1′、2′、3′、4′为蜗杆螺旋面Σ₁二次接触线，其上各点的φ值不同：φ＞φ₁，且由左下端到右上端φ值逐渐减小，两条瞬时接触线相交于N线，交点处φ=φ₁，例如4′和4的交点处。蜗杆齿面Σ₁的单位法矢量由齿的空域指向实体，φ＞φ₁时，曲率干涉界限函数Ψ＞0，无干涉，瞬时接触线留在蜗轮齿面Σ₂上；而瞬时接触线1′、2′、3′、4′延伸过N线的部分，φ＜φ₁时，曲率干涉界限函数Ψ<0，有干涉，于是瞬时接触线1′、2′、3′、4′在N线右侧的部分被切去，瞬时接触线1′、2′、3′、4′在蜗轮齿面Σ₂上N线左边接触区Σ_2B内，Σ_2B称为新接触区。原接触区Σ_2A和新接触区Σ_2B沿瞬时接触线奇点轨迹曲线N光滑相切。

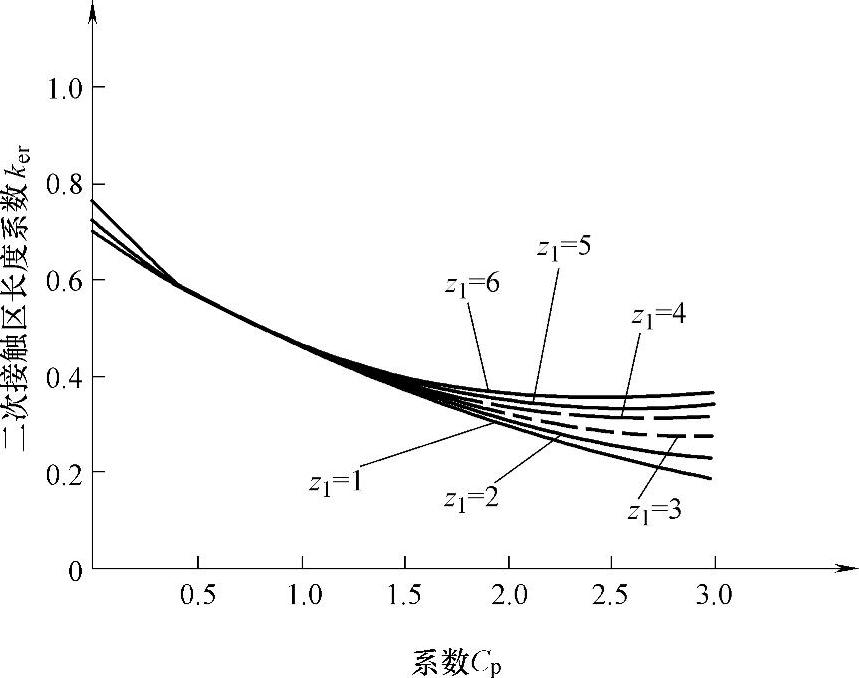
图8-15 不同蜗杆头数z₁时C_p与蜗轮二次接触区蜗杆啮合长度系数k_er关系曲线图

由8.3节中的公式可算出蜗杆和蜗轮接触区的各种界线，利用8.3节中的方法进行蜗轮齿面结构分析。

图8-5上部为蜗轮齿面上瞬时接触线族{Γ₂}分布状况：1、2、3、4为原接触区Σ_2A上的瞬时接触线；1′、2′、3′、4′为新接触区Σ_2B上的瞬时接触线。由齿顶向齿根取点a、b、c为瞬时接触线上微观啮合质量参数

θ_vt和

的计算点。

图8-5中部为蜗轮齿面接触区及其界线。图8-5下部为啮合面上各界线在（O₀₁；y₀₁，z₀₁）坐标平面上的投影。

蜗轮齿面由接触区（Σ_2A+Σ_2B）和前过渡曲面C₁构成，其结构如下：

1）IJFE：蜗轮齿面上的原接触区Σ_2A（φ=φ₁）。

2）EFDC：原接触区内的蜗轮齿面二次接触区。

3）EFHG：蜗轮齿面上的新接触区Σ_2B（φ≥φ₁）。

4）EF：蜗轮齿面上瞬时接触线奇点轨迹曲线N；Σ_2A和Σ_2B沿N线相切。

5）AB：接触区Σ_2A与前过渡曲面C₁的切线（在蜗轮齿面之外）。

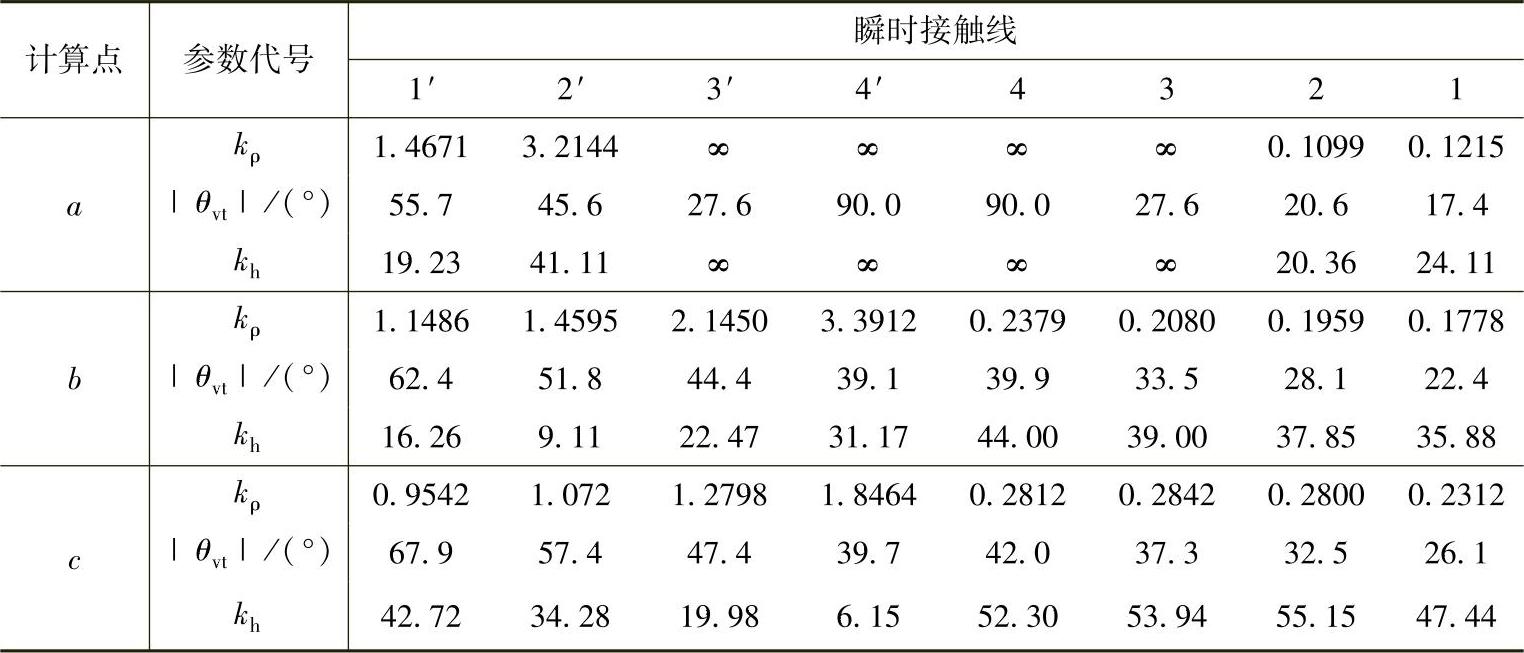
双自由度直线标准环面蜗杆传动的齿面接触点微观啮合质量参数kρ、θ_vt和k_h的计算结果：z₁=1，C_p=1.5（见图8-16d）见表8-6；z₁=6，C_p=1.0（见图8-21b）见表8-7。

表8 - 6 双自由度直线标准环面蜗杆传动的齿面接触点微观啮合质量参数k_ρ、|θ_vt|和k_h值（z₁=1，C_p=1.5（见图8-16d））

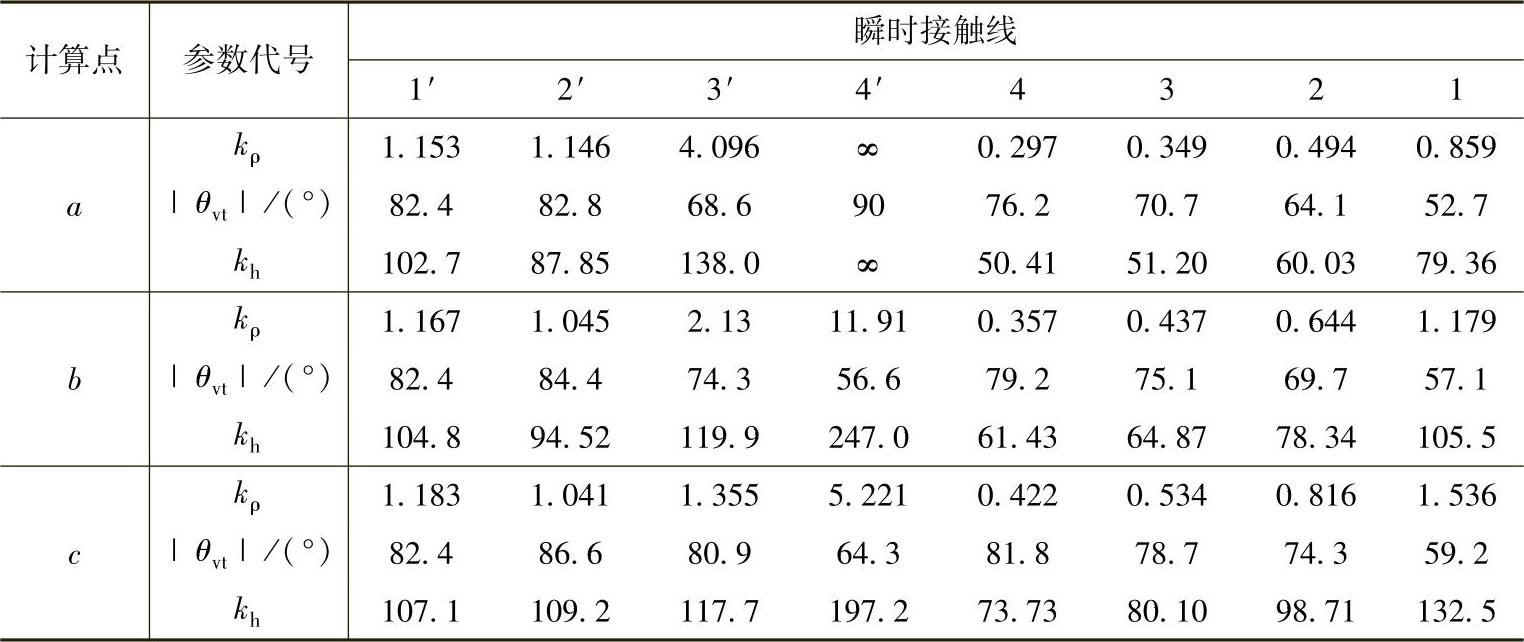
表8 - 7 双自由度直线标准环面蜗杆传动的齿面接触点微观啮合质量参数k_ρ、|θ_vt|和k_h值（z₁=6，C_p=1.0（见图8-21b））(www.xing528.com)

从图8-5可以看到：标准传动啮合面的界线在（O₁；y₀₁，z₀₁）坐标平面上的投影围成的啮合区呈“Y”字形，“Y”字又分成啮入端的“V”字和啮出端的“I”字；“V”字和“I”字由蜗轮齿面接触线奇点轨迹曲线N的投影线连接。蜗杆工作长度L_w一定时，曲线N的位置确定了“V”字和“I”的长短：“V”为双线接触区，其长度越长，瞬时接触线总长l越长，啮合质量越好；“I”与蜗轮齿面二次接触区对应，蜗轮齿面易点蚀，“I”越长宏观啮合质量越差。

蜗杆上双线接触区长度l_s与蜗杆工作长度L_w的比例，称为双线接触区长度系数k_L。鉴于双线接触区的左线接触区和右线接触区长度一般不相同，取左线接触区和右线接触区二者中长度大者作为双线接触区长度l_s。

双线接触区长度计算起点为N曲线与蜗杆齿顶环面的交点F，点F在计算蜗杆切齿啮合界线中已求得，其在坐标系（O₁；y₀₁，z₀₁）里的z₀₁值记为z_01F。左、右线终点的计算：以E点为初值，一直计算到相应的终点。

（1）右线——原接触区

计算表8-2中点I和点A在坐标系（O₁；y₀₁，z₀₁）里的z₀₁值z_01I和z_01A，在（z_01I-z_01F）和（z_01A-z_01F）中的较小值为右线接触区长度l_sr，即

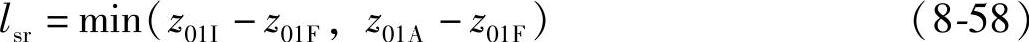
（2）左线——新接触区

计算表8-2中点G和点A′在坐标系（O₁；y₀₁，z₀₁）里的z₀₁值z_01G和z_01A′，在（z_01G-z_01F）和（z′_01A-z_01F）中的较小值为右线接触区长度l_sl，即

l_s1=min（z_01G-z_01F，z′_01A-z_01F） （8-59）

取右接触区长度和左接触区长度中大者作为双线接触区长度

l_s=max（l_sr，l_sl） （8-60）

图8-16为蜗杆头数z₁=1和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-16a、b、c、d、e和f分别为C_p取0.0、0.5、1.0、1.5、2.0、2.5时的图。

图8-17为蜗杆头数z₁=2和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-17a、b、c、d和e分别为C_p取0.0、0.5、1.0、1.5、2.0时的图。

图8-18为蜗杆头数z₁=3和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-18a、b、c和d分别为C_p取0.5、1.0、1.5、2.0时的图。

图8-19为蜗杆头数z₁=4和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-19a、b、c和d分别为C_p取0、0.5、1.0、1.5时的图。

图8-20为蜗杆头数z₁=5和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-20a、b和c分别为C_p取0.5、1.0、1.5时的图。

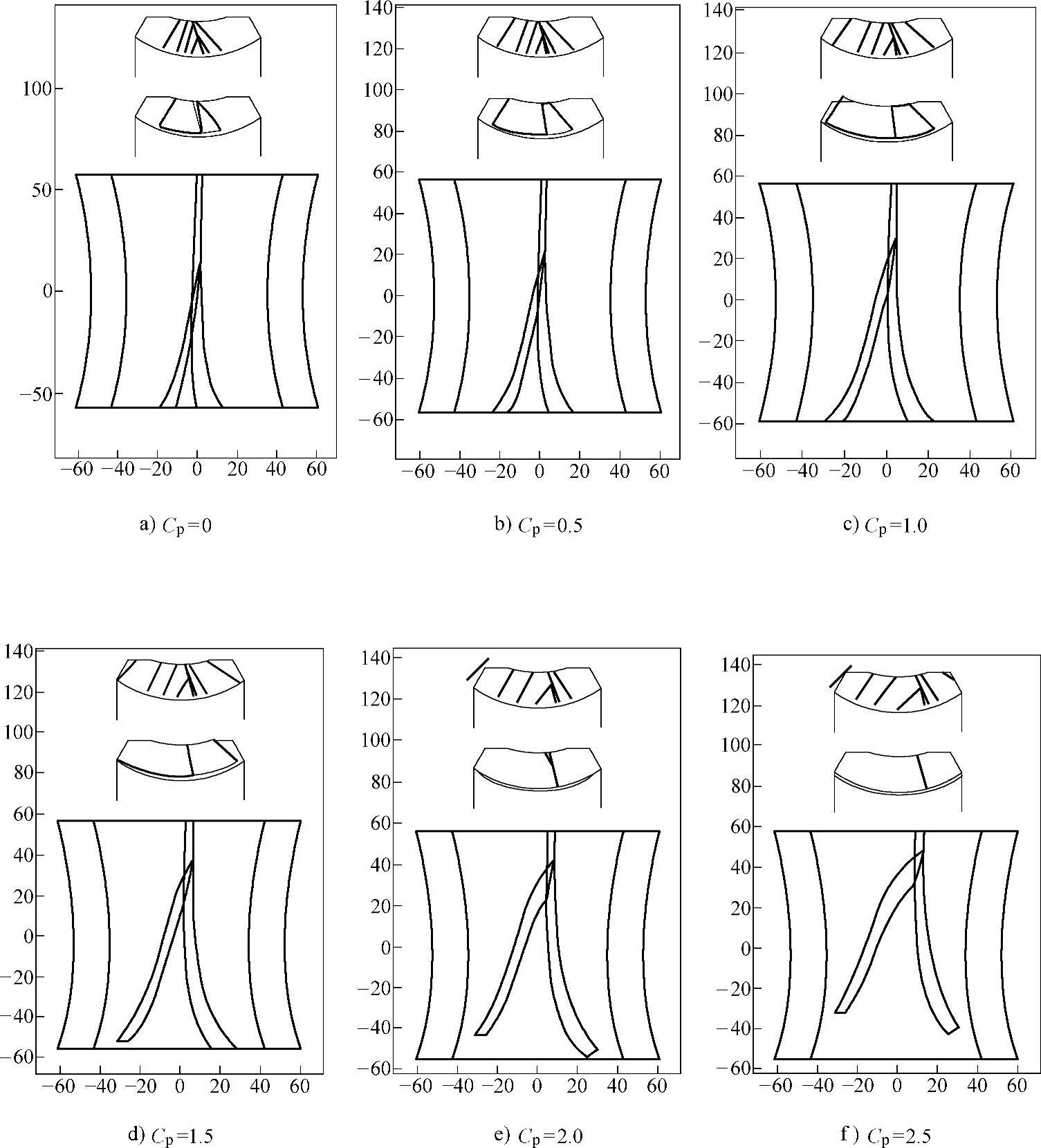
图8-16 蜗杆头数z₁=1和不同C_p时接触区以及瞬时接触线分布情况图

图8-21为蜗杆头数z₁=6和不同C_p时的蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况图，其中图8-21a、b和c分别为C_p取0.9、1.0、1.5时的图。

表8-8为不同蜗杆头数和C_p对应的蜗杆齿面上双线接触区长度l_s及其长度系数k_L对照表。

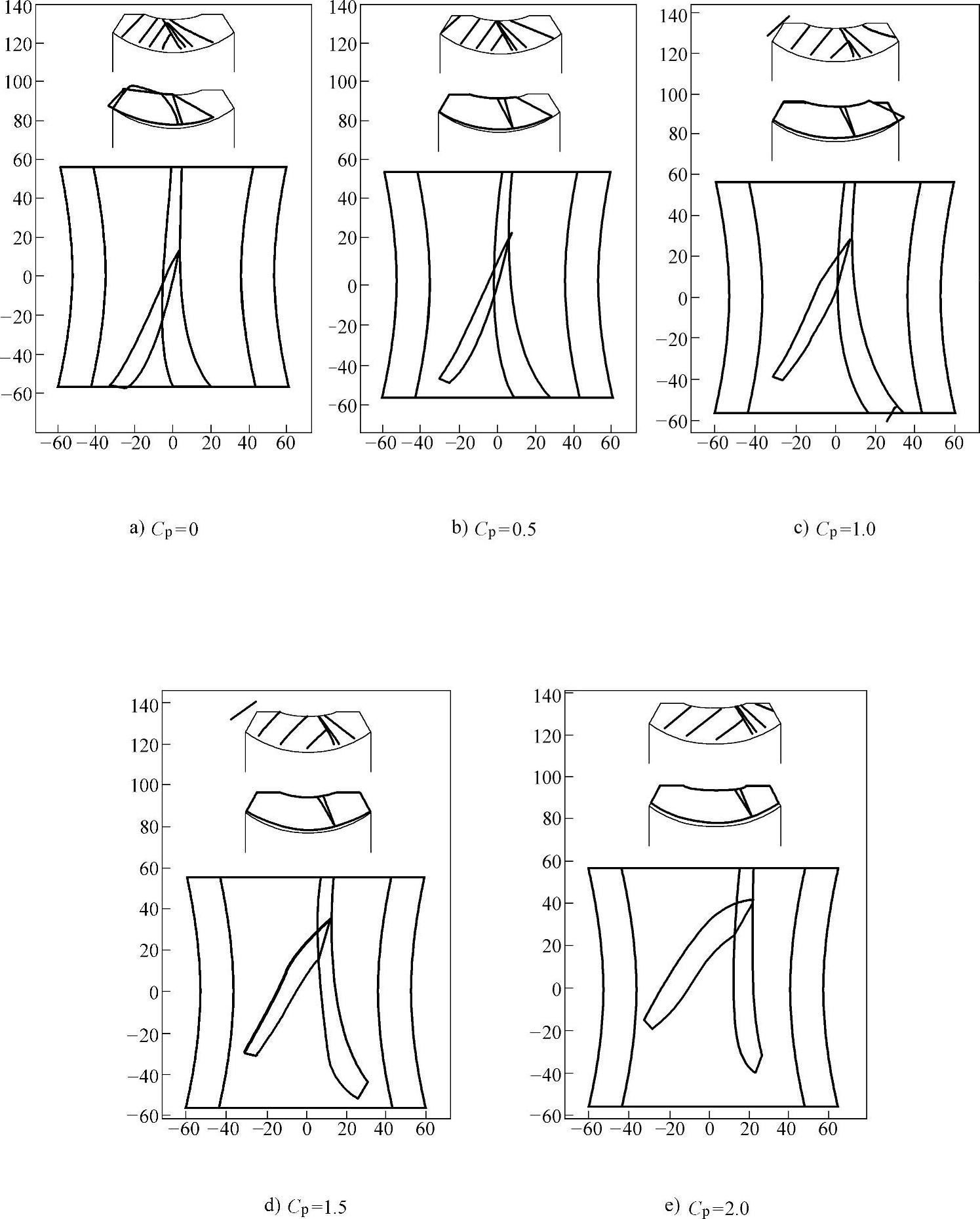
图8-17 蜗杆头数z₁=2和不同C_p时接触区以及瞬时接触线分布情况图

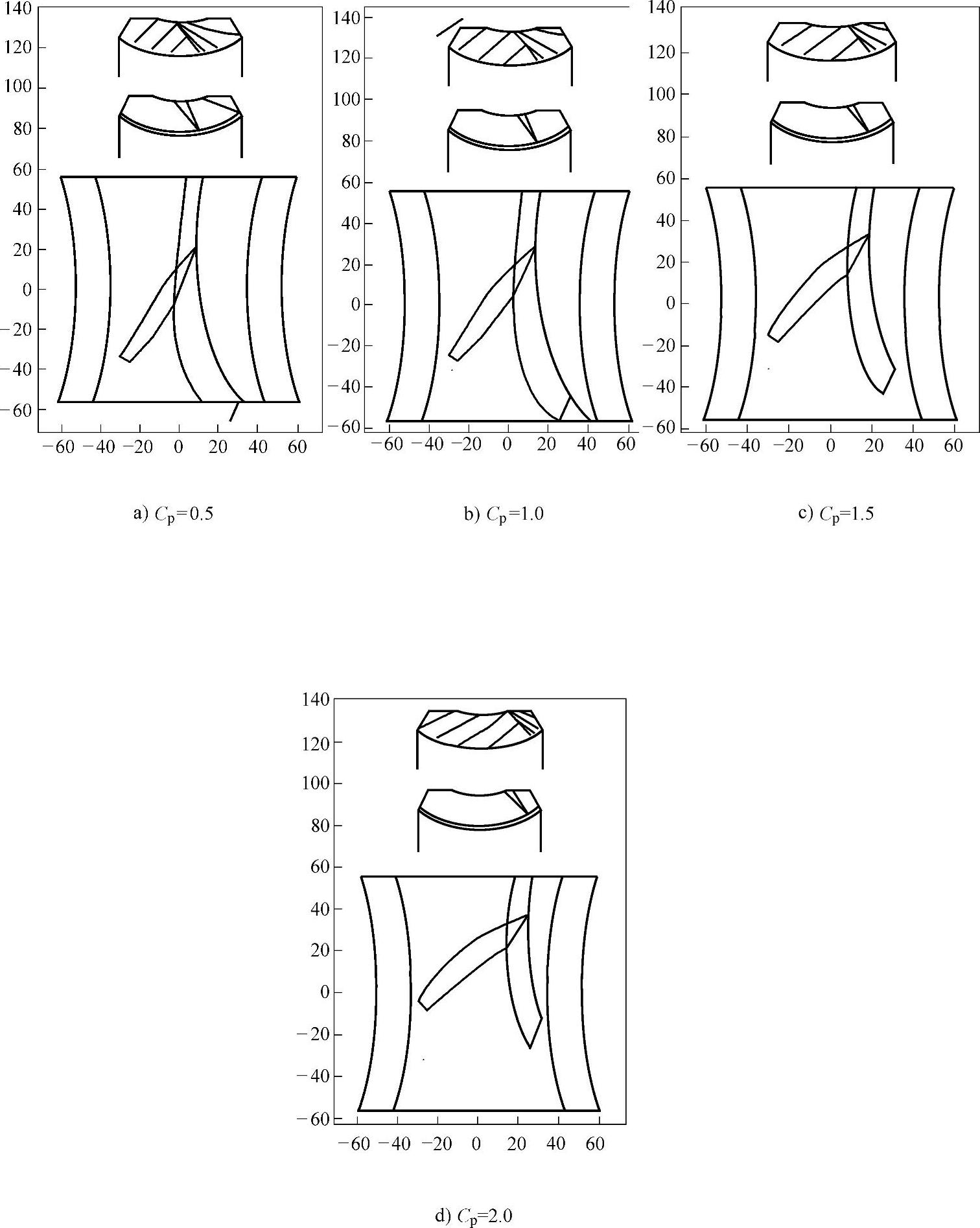
图8-18 蜗杆头数z₁=3和不同C_p时接触区以及瞬时接触线分布情况图

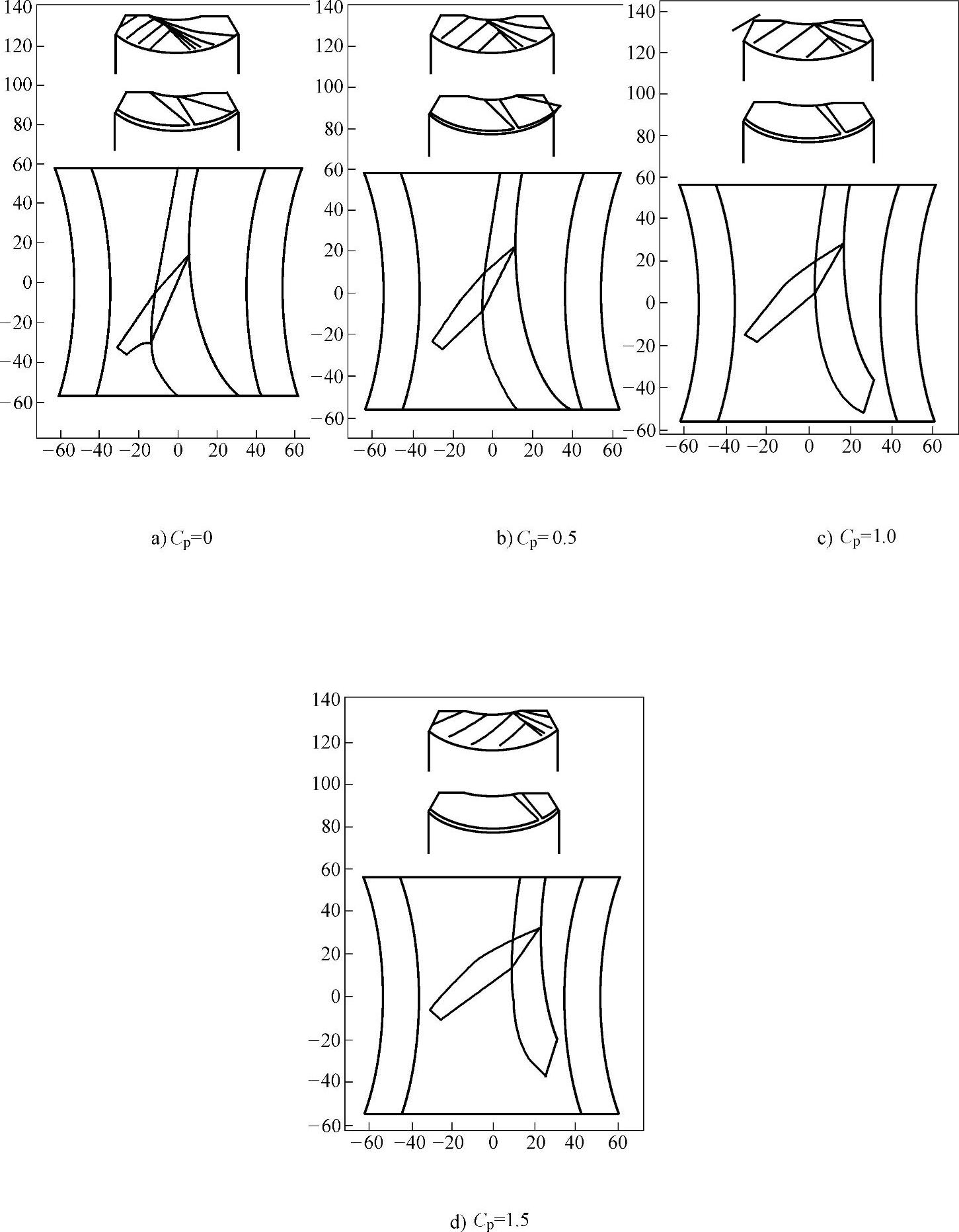
图8-19 蜗杆头数z₁=4和不同C_p时接触区以及瞬时接触线分布情况图

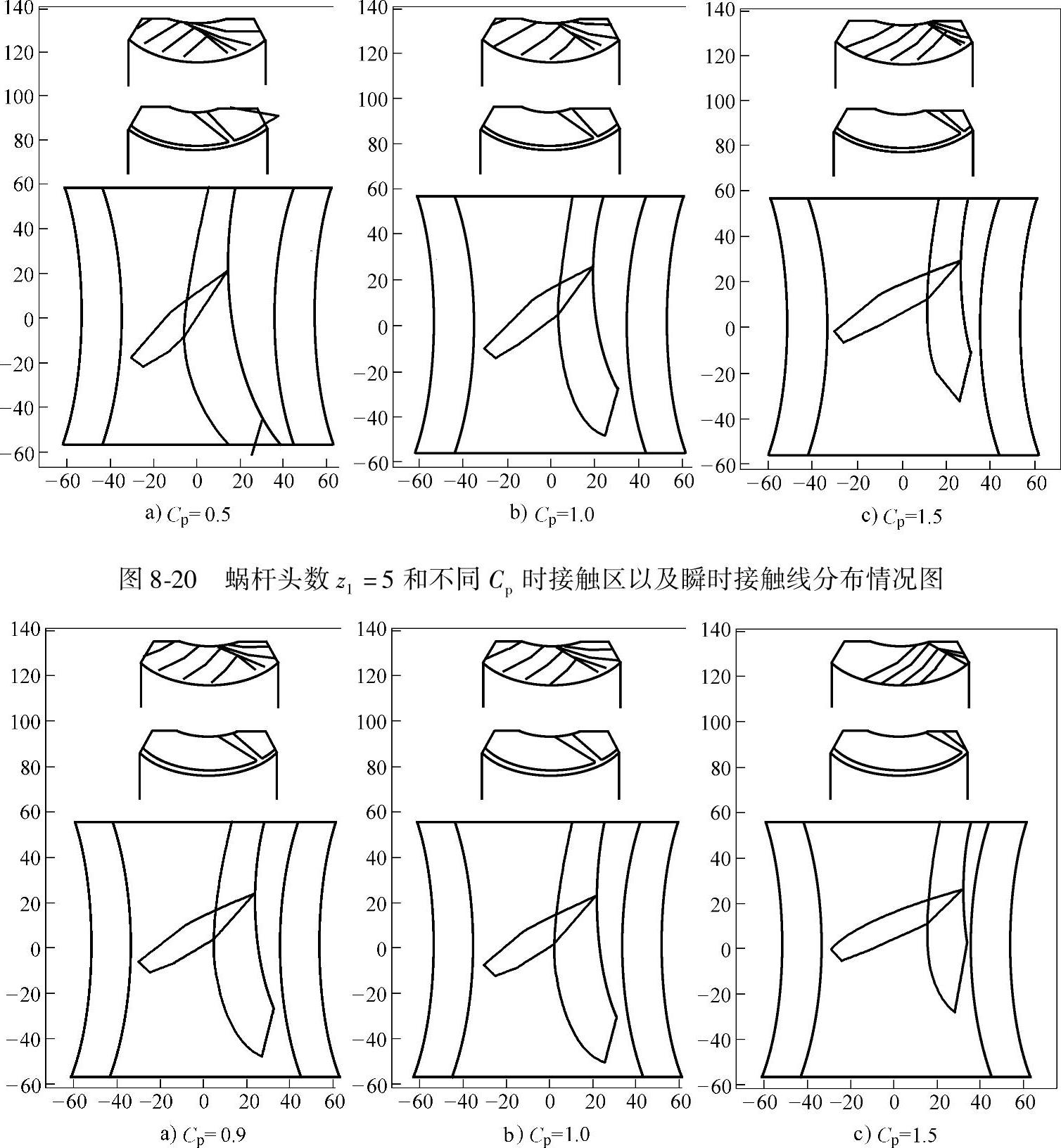
图8-21 蜗杆头数z₁=6和不同C_p时接触区以及瞬时接触线分布情况图

表8 - 8 蜗杆头数z₁和系数C_p与双线接触区长度l_s及其长度系数k_L对照表

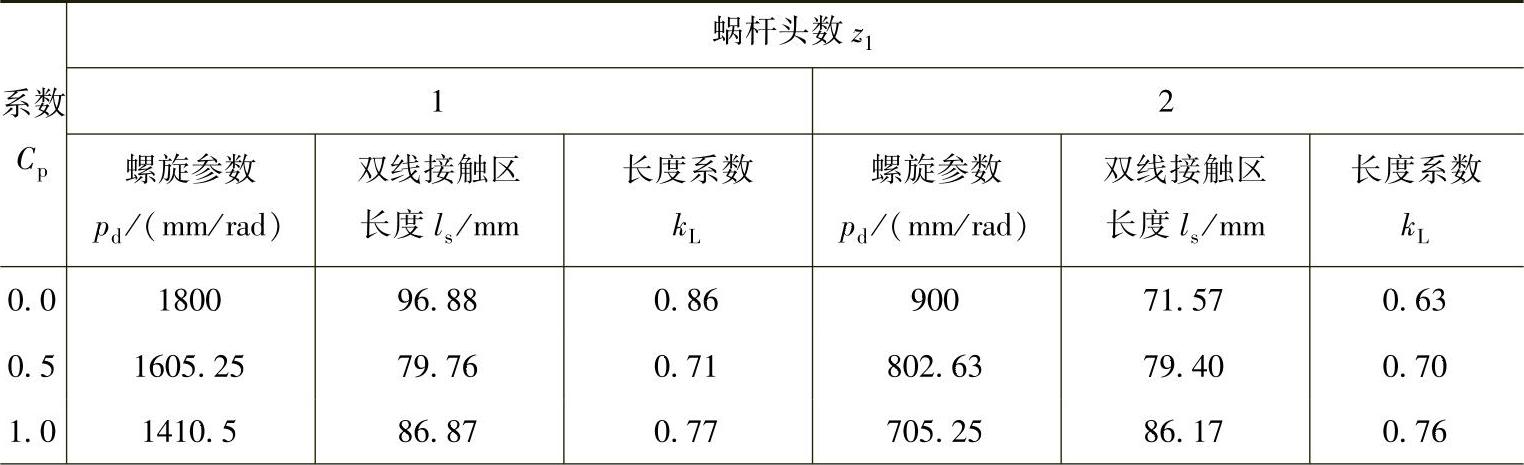
（续）

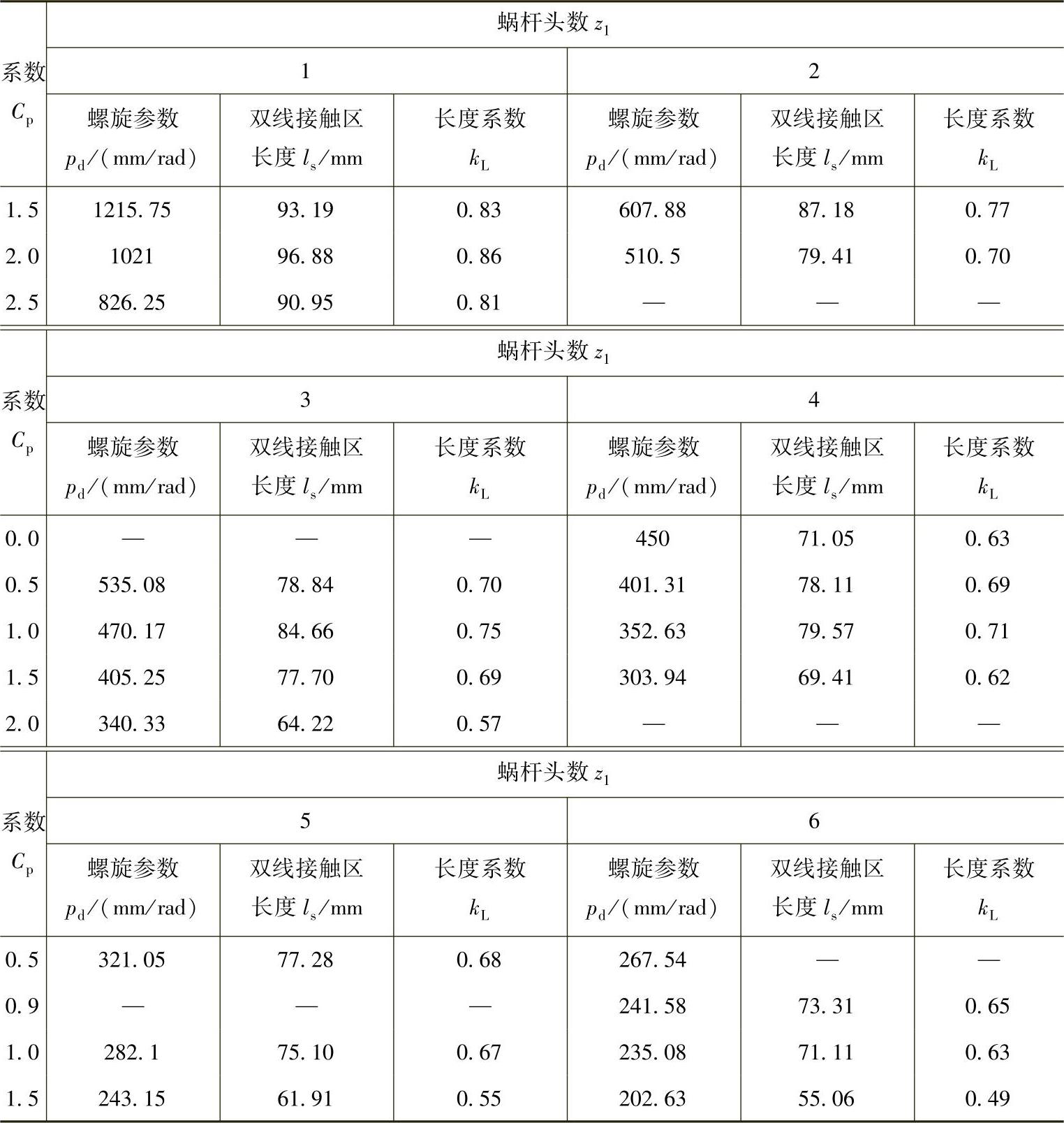
图8-22为不同蜗杆头数z₁时系数C_p与双线接触区长度系数k_L的关系曲线图。

由表8-8和图8-22可以看出，在C_p=0.5附近，不同蜗杆头数对应的双线接触区长度系数相近，大约为0.70；z₁=1、C_p=0.5～2.0时，对应的双线接触区长度系数增大，最大值约为0.86；z₁=2、C_p=0.5～1.4时，对应的双线接触区长度系数增大，最大值约为0.77；z₁=3、C_p=0.5～1.0时，对应的双线接触区长度系数增大，最大值约为0.75；z₁=4、C_p=0.5～0.8时，对应的双线接触区长度系数增大，最大值约为0.71；z₁=5和6、C_p＞0.5时，对应的双线接触区长度系数减小。

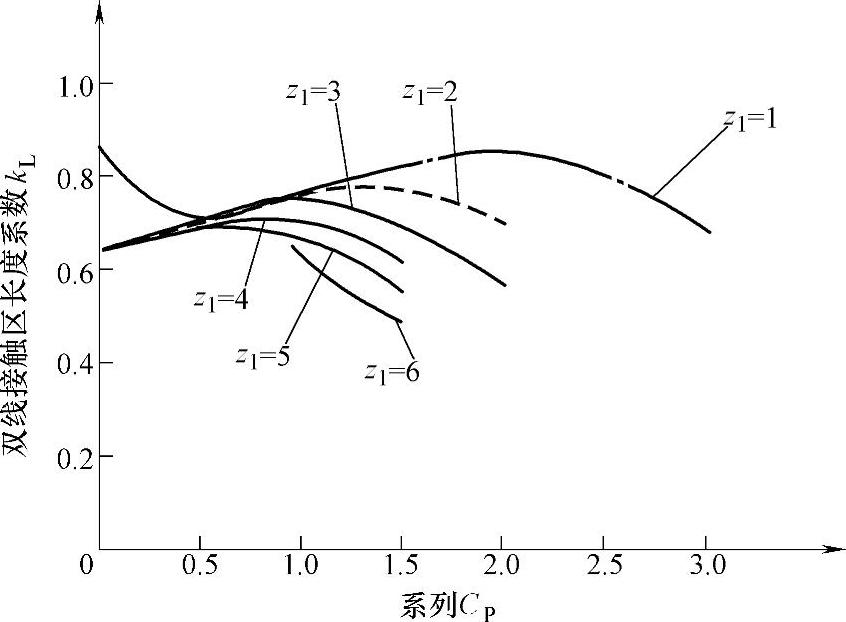
图8-22 不同蜗杆头数z₁时系数C_p与双线接触区长度系数k_L的关系曲线图

5.蜗杆直径d₁对蜗杆根切界线、边齿顶厚度和对蜗杆双线接触区和蜗轮齿面接触区的影响研究

（1）蜗杆头数为z₁=4、5、6时的情形

对于多头数的蜗杆，通过增大蜗杆分度圆直径d₁，研究蜗杆分度圆直径d₁对蜗杆根切界线、边齿顶厚度以及双线接触区长度及其系数的影响。如z₁=6时，C_p=1.0，参照附表1，取蜗杆分度圆直径d₁的第2系列值d₁=100mm，以及为了使增大蜗杆分度圆直径的效果明显，取d₁=120mm，分别得到蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况如图8-23a、b所示。表8-9为蜗杆头数z₁=6、系数C_p=1.0和不同蜗杆分度圆直径d₁时双线接触区长度l_s及其长度系数k_L对照表。

表8 - 9 蜗杆头数z₁=6、系数C_p=1.0和不同蜗杆分度圆直径d₁时双线接触区长度l_s及其长度系数k_L对照表

由图8-23和表8-9知：取C_p=1.0时，随着蜗杆直径d₁增大，双线接触区长度也增大。

当蜗杆头数z₁=6、d₁=120mm，分别取C_p=0、0.5、1.0、1.5和2.0时，展成蜗杆曲率干涉界线在蜗杆轴截面上的位置如图8-24所示，由该图知：C_p≥0.0时，蜗杆不根切。

当蜗杆头数z₁=6、d₁=120mm和C_p=1.0时，边齿顶变尖。通过齿顶圆弧修正，取蜗杆齿顶圆弧和分度圆弧偏心距e=53.18mm，得到边齿顶宽度为3.325mm，为蜗轮端面模数m_t的0.35倍，即边齿顶不变尖。边齿高为14.29mm，比原边齿高16.15mm只降低了1.86mm。

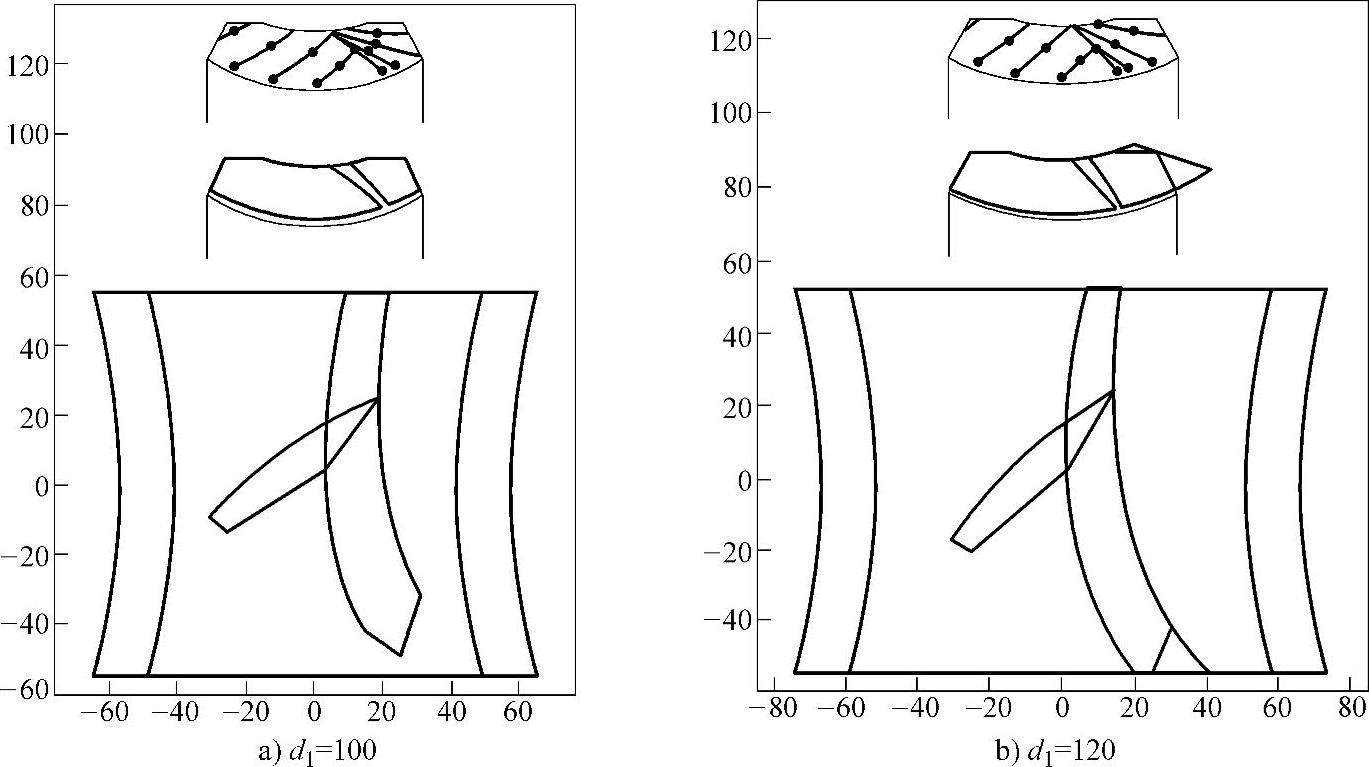
图8-23 蜗杆头数z₁=6、系数C_p=1.0和不同蜗杆直径d₁时接触区以及瞬时接触线分布情况图

（2）蜗杆头数为z₁＞6时的情形

上述其他参数不变，只是将蜗杆头数增加至z₁=10，得到蜗轮和蜗杆上的接触区以及蜗轮上瞬时接触线分布情况如图8-25所示，此时，双线接触区长度l_s=67.77mm，长度系数为k_L=0.65。

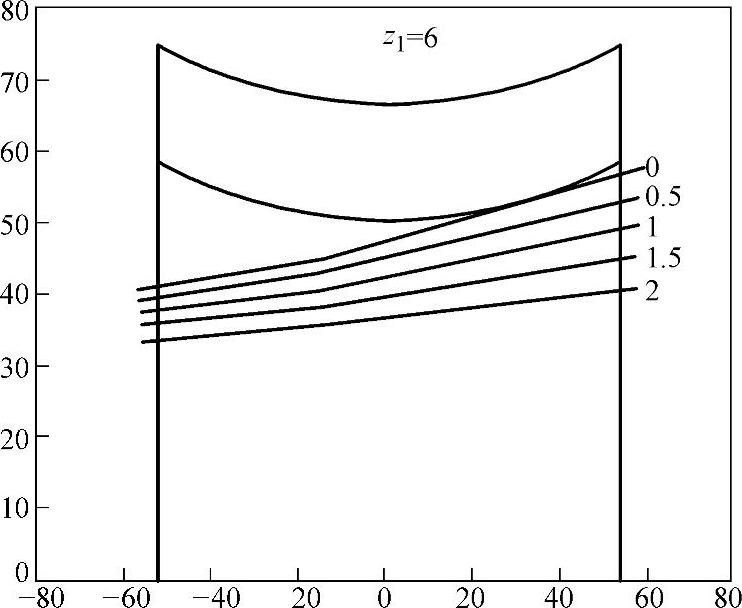
图8-24 蜗杆头数z₁=6和不同C_p时展成蜗杆曲率干涉界线ψ_d在蜗杆轴截面上的位置图

分别取C_p=0、0.5、1.0、1.5和2.0，展成蜗杆时曲率干涉界线在蜗杆轴截面上的位置如图8-26所示，由该图知：C_p≥0.6时，蜗杆不根切。

当C_p=1.0时，边齿顶变尖。通过齿顶圆弧修正，取蜗杆齿顶圆弧和分度圆弧偏心距e=242.55mm，得到边齿顶厚度为3.325mm，为蜗轮端面模数m_t的0.35倍，即边齿顶不变尖。边齿高为11.58mm，比原边齿高16.15mm降低了4.57mm。

因此，对于多头的双自由度直线环面蜗杆副，可以通过增大蜗杆分度圆直径d₁来增大双线接触区长度及其系数，这样蜗杆的头数z₁可做得更大。

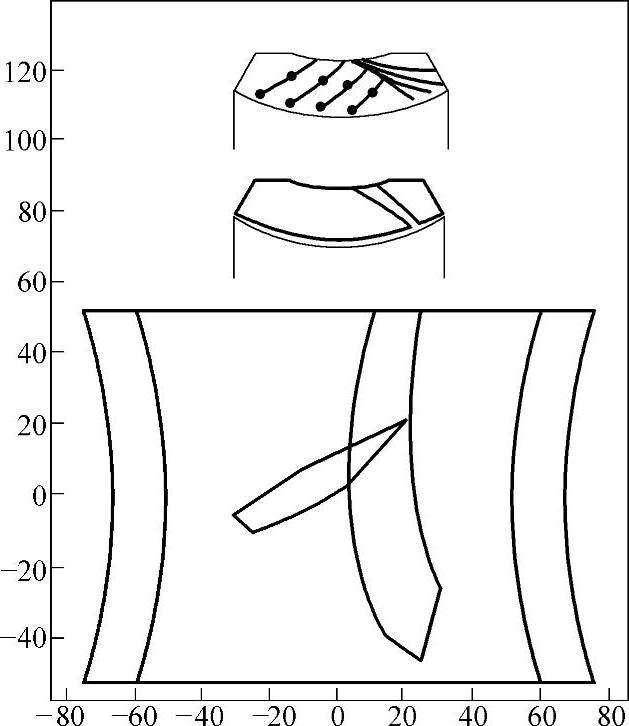
图8-25 蜗杆头数z₁=10、系数C_p=1.0和蜗杆直径d₁=120mm时接触区以及瞬时接触线分布情况图

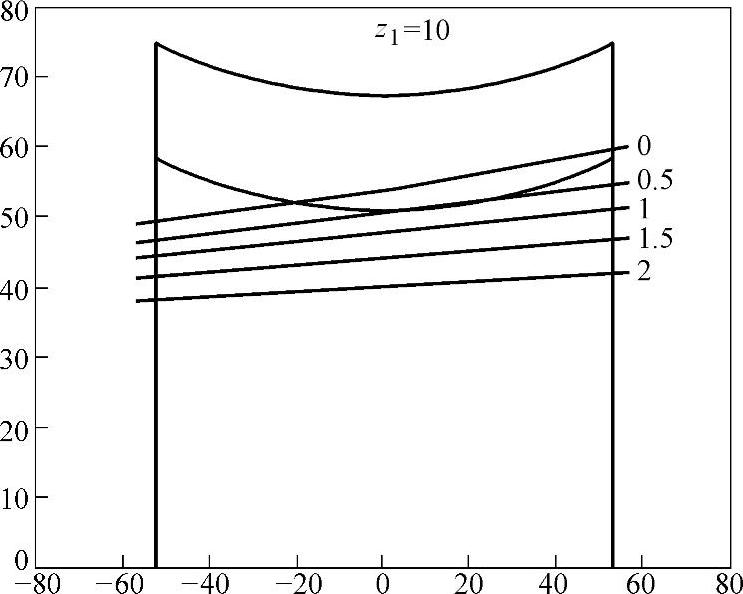
图8-26 蜗杆头数z₁=10和不同C_p时展成蜗杆曲率干涉界线ψ_d在蜗杆轴截面上的位置图