如何优化蜗杆的边齿顶厚度？

1.蜗杆轴平面齿廓

在坐标系σ₁里，环面蜗杆螺旋面Σ₁的方程见式（6-64），任取一蜗杆的轴平面T（见图8-7）。取坐标系σ_t（O_t；i_t，j_t，k_t），i_t和k_t在轴平面T上，其中k_t=k₁，i_t至i₁的有向角为μ，由图8-7可求得

tanμ=-y₁/x₁ （8-30）

σ₁相对于σ_t逆时针转动，μ为正值。σ₁→σ_t坐标变换回转矩阵为R[k_t，μ]，在蜗杆轴平面T内得到环面蜗杆齿廓方程为

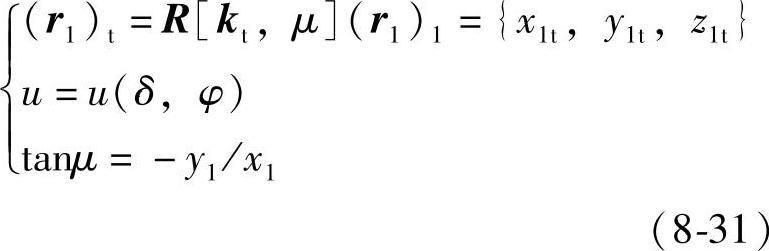
改变μ值，蜗杆轴平面T的位置改变，由式（8-31）可求得环面蜗杆由μ值确定的轴平面内的齿廓。

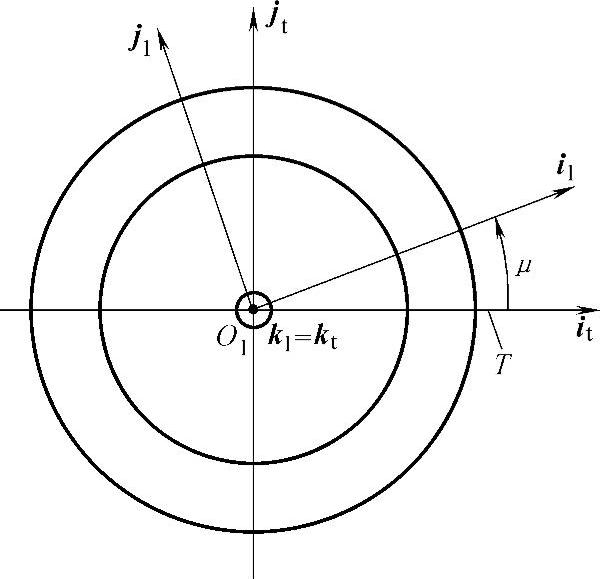
图8-7 环面蜗杆轴平面T在σ₁里的位置

2.蜗杆喉部分度圆齿厚

加工环面蜗杆时，需要在其喉部测量分度圆法向齿厚s_n1，这在环面蜗杆传动几何计算时已求得。计算环面蜗杆边齿顶厚时，需要知道蜗杆轴平面T内分度圆弧齿厚s₁值。按直廓环面蜗杆计算分度圆弧齿厚^[15]为

s₁=πd₂γ₁/180° （8-32）

3.环面蜗杆的边齿顶厚

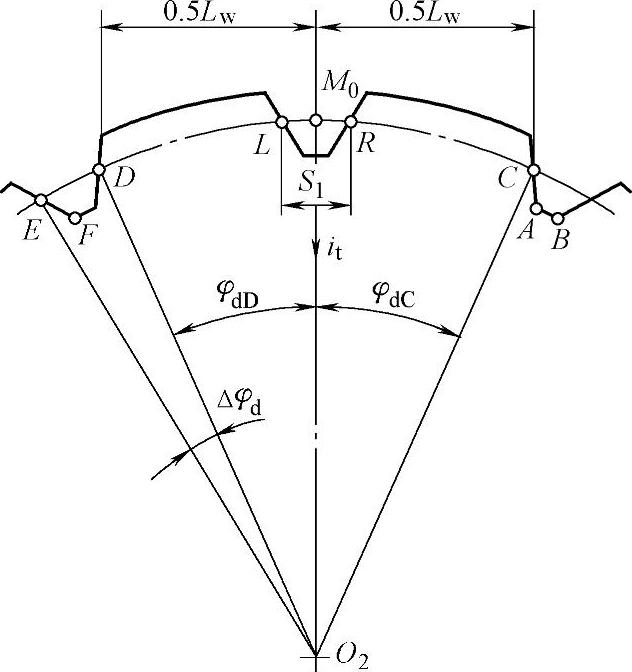
如图8-8所示，环面蜗杆轴平面T与蜗轮中间平面重合。边齿齿廓位置由蜗杆工作长度L_w确定。

蜗杆分度圆环面上的点满足

（a-x_t）2+z²_t=0.25d²₂ （8-33）

蜗杆齿顶圆环面上的点满足

（a-x_t）2+z²_t=R²_a1 （8-34）

蜗杆边齿左侧齿廓与分度圆环面交点C处有

z_t=0.5L_w （8-35）

将式（8-33）、式（8-35）和式（8-31）联立求解，可得到μ_C值。刀座相应转角为φ_dC。

将μ_C值代入式（8-31），再与式（8-34）联立求解，得齿顶点A的坐标值（x_tA，0，z_tA）。

需要求出边齿右侧齿顶点B的坐标值。通常蜗杆喉部中间平面两侧蜗杆螺旋面对称，由于点B与点F对称于i_t，求出图8-8中左侧边齿顶点F的坐标值（x_tF，0，z_tF），即可得到点B的坐标值（x_tF，0，-z_tF）。

环面蜗杆左侧齿廓点D处有

z_t=-0.5L_w （8-36）

式（8-33）、式（8-36）与式（8-31）联立求解，可得

μ_D=-μ_C （8-37）

环面蜗杆喉部左侧齿廓L点处有

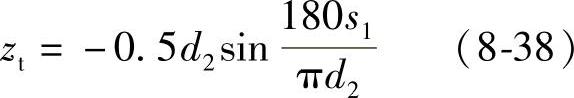
将式（8-38）、式（8-33）与式（8-31）联立求解可得到μ_L值。

(www.xing528.com)

图8-8 环面蜗杆在蜗轮中间平面内的边齿顶厚

图8-8中在环面蜗杆的左端，两侧齿廓点D和点E之间分度圆弧的圆心角为齿厚角，即

Δφ_d=i_d1Δμ=2i_d1μ_L （8-39）

于是点E处，轴平面T到i₁的有向角为

μ_E=μ_D+Δμ=-μ_C+2μ_L （8-40）

将μ_E代入式（8-31），然后与式（8-34）联立求解，得到点F的坐标值（x_tF，0，z_tF），从而得到点B的坐标值（x_tF，0，-z_tF）。

环面蜗杆的边齿顶厚为

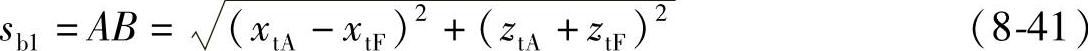
令环面蜗杆的边齿顶厚系数为

则s_b1=k_sm_t

4.蜗杆边齿顶变尖时齿顶圆弧半径的修正

蜗杆头数较多或刀刃运动的螺旋参数p_d不合适时，易出现边齿顶变尖。这不仅使蜗杆边齿的强度降低，使滚刀难于制作，而且边齿顶寿命短。

为了增大蜗杆边齿顶厚，使k_s≥0.35，比较简便而又有效的方法是降低环面蜗杆边齿顶高，把齿顶变尖部分切去。

如图8-9所示，使蜗杆齿顶圆弧与分度圆弧偏心，偏心距为e。蜗杆喉部齿顶高不变，蜗杆齿顶圆弧半径修正为

R′_a1=R_a1+e （8-43）

式（8-34）改写成

（a+e-x_t）2+z²_t=（R_a1+e）² （8-44）

要求修正后的边齿顶厚为

s_b1=0.35m_t （8-45）

计算边齿顶点A和F的坐标时用式（8-44），由式（8-45）迭代求解偏心距e值。具体迭代方法：可以逐步增加e的值来计算s_b1，直到找到s_b1=0.35m_t。但每次e增加多少不好确定，而已知e的取值区间是（0，e_max），则可以采用二分法，逐步缩短区间。因为增加e，实际上求的点A和点F分别更向点C和点E靠近（见图8-8），所以初值也没问题。

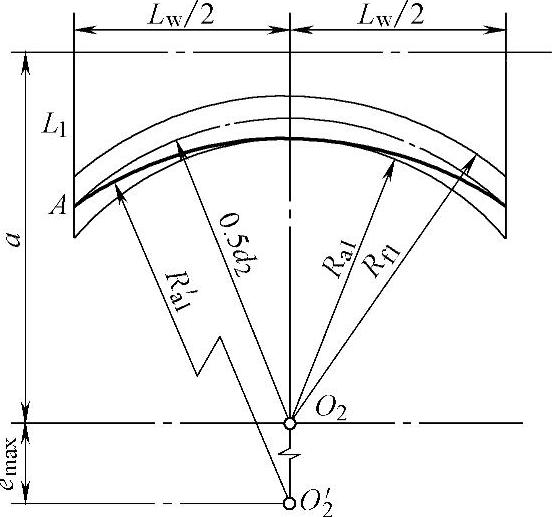
图8-9 环面蜗杆齿顶圆弧半径的修正示意图

e_max的给定：只有分度环面上喉部齿厚s₁已给定，而且s₁已远远超过m_t，所以增加偏心距e使s_b1=0.35m_t，蜗杆齿顶圆弧才不会达到蜗杆分度圆弧与蜗杆端面L₁的交点A（见图8-9）。将蜗杆齿顶圆弧通过点A时的对应的e作为e_max。

在蜗杆图示的轴平面内有

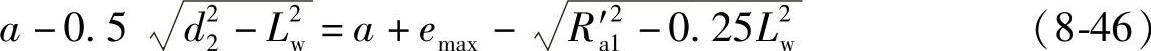
将R′_a1=R_a1+e_max代入式（8-46）解得

蜗杆边齿顶变尖时，要修正齿顶圆弧半径，实际上只改变点A和点F，而点C、L、D和E都不变。所以只将计算点A、点F和计算边齿顶厚的程序单列出来，以便循环计算用，而点C、L、D和E的计算不用循环。