齿面接触区边界的分析与应用

第6章研究了展成蜗杆时虚拟产形面Σ_d上的啮合界线Φ_dφ、环面蜗杆螺旋面Σ₁及其上的曲率干涉界线Ψ_d，第7章研究了展成蜗轮时环面蜗杆螺旋面Σ₁上的啮合界线Φ_φ1、蜗轮齿面Σ₂及其上的曲率干涉界线Ψ和瞬时接触线奇点轨迹曲线N以及瞬时接触线，这些界线在一定条件下才会在蜗杆螺旋面和蜗轮齿面上出现。

蜗杆螺旋面和蜗轮齿面有一定的高度和宽度，齿面接触区被限制在这个高度和宽度范围内；残留的前、后过渡曲面又覆盖掉蜗轮齿面接触区的一部分。因此，需要计算出接触区边界，确定这些曲线是否在蜗杆螺旋面和蜗轮齿面上，以及在蜗杆螺旋面和蜗轮齿面上的位置，绘制接触区图形，以便进行宏观啮合质量评价。

为了使接触区图形直观、清楚地表达接触区在蜗杆螺旋面和蜗轮齿面上的位置及对应关系，在蜗轮轴截面内坐标系（O₂；R_B，z₀₂）里绘出蜗轮齿面的边界线，将蜗杆齿面接触区的边界线投影到（O₁；y₀₁，z₀₁）坐标平面上。

图8-2为蜗杆螺旋面边界：半径R_a1的蜗杆齿顶圆弧为螺旋面顶部的边界，由它确定蜗轮齿根部的接触区边界线；由蜗杆工作长度L_w确定的垂直于蜗杆轴线的平面与蜗杆螺旋面的交线为R₁和L₁。对于滚刀而言：R₁为啮入端近似的第一刀刃，加工出蜗轮的前过渡曲面C₁；L₁为啮出端近似的末刀刃，加工出蜗轮的后过渡曲面C₂。对于蜗杆而言，由交线R₁确定接触区与前过渡曲面C₁的切线，由交线L₁确定接触区与后过渡曲面C₂的切线。

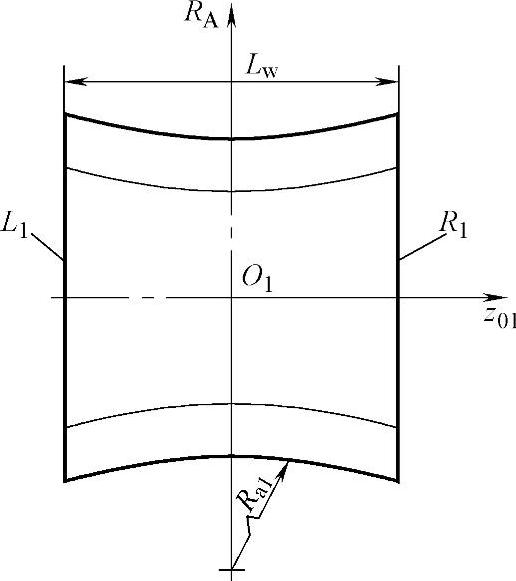
图8-2 蜗杆螺旋面的边界图

图8-3为蜗轮齿面的边界：半径为R_a2圆弧形成的圆环面和直径为d_ea2的圆柱面构成蜗轮齿顶面，由它确定蜗杆螺旋面根部的接触区边界线；蜗轮两端30°倒角，锥面R₂和L₂确定蜗杆啮入端的边界线。

1.蜗杆螺旋面的边界条件

（1）蜗杆齿顶圆弧的边界条件

图8-2取坐标系（O₁；z₀₁，R_A），蜗杆齿顶环面上的点必须满足下面条件：

（a-R_A）²+z²₁-R²_a1=0 （8-1）

式中R_A见式（7-97）。

（2）蜗杆啮入端R₁的边界条件

如图8-2所示，由蜗杆工作长度L_w得到

z₁=0.5L_w （8-2）

（3）蜗杆啮出端L₁的边界条件

如图8-2所示，由蜗杆工作长度L_w得到

z₁=-0.5L_w （8-3）

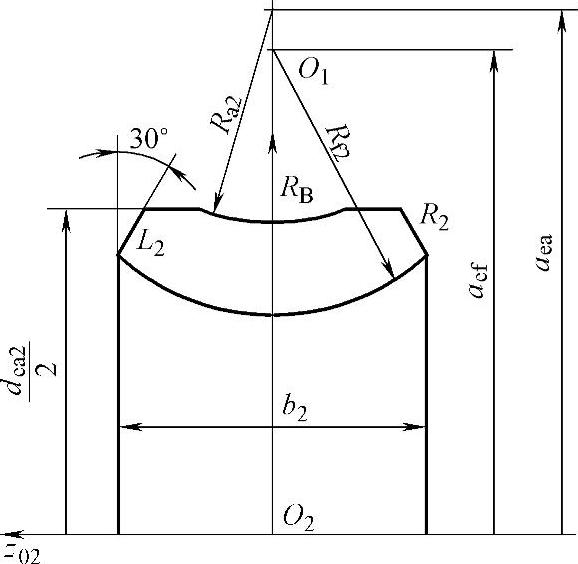
图8-3 蜗轮齿面的边界

2.蜗轮齿面的边界条件

（1）蜗轮齿顶圆弧的边界条件

图8-3取坐标系（O₂；z₀₂，R_B），蜗轮齿顶环面上的点必须满足下面条件：

（a_ea-R_B）2+z²₂-R²_a2=0 （8-4）

a_ea=0.5d_a2+R_a2 （8-5）

式中R_B见式（7-99）。

（2）蜗轮齿根圆弧的边界条件

如图8-3所示，在坐标系（O₂；z₀₂，R_B）里，蜗轮齿根环面上的点必须满足下面条件：

（a_ef-R_B）2+z²₂-R²_f2=0 （8-6）

R_f2=0.5d_a1+c （8-7）

a_ef=0.5d_f2+R_f2 （8-8）

（3）蜗轮外圆边界条件

如图8-3所示，由蜗轮齿顶圆最大直径d_ea2得到

R_B=0.5d_ea2 （8-9）

（4）蜗轮R₂端倒角锥面的边界条件

由图8-3得到

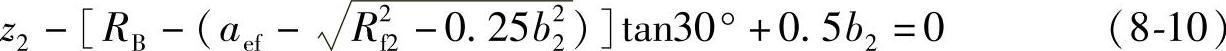
（5）蜗轮L₂端倒角锥面的边界条件(www.xing528.com)

由图8-3得到

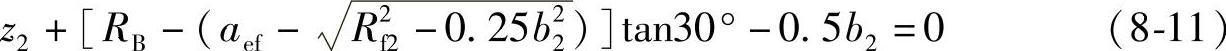
3.界线的求解

啮合界线、曲率干涉界线和接触线奇点轨迹曲线的方程在第7章里已得到。齿面接触区各边界条件方程与啮合面方程联立求解，即可得到啮合面上接触区边界线。再将各界线变换到坐标系（O₂；R_B，z₀₂）里，绘出蜗轮轴线截面内接触区边界线；变换到坐标系（O₁；y₀₁，z₀₁）里，绘出啮合面边界的投影。

为了清楚地表达蜗轮齿面上界线各界点，给各界点命名，如图8-4所示。其中点G′满足式（8-9）和下式：

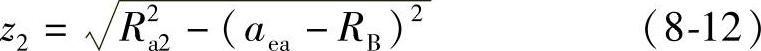
点I′满足式（8-9）和下式：

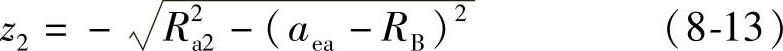
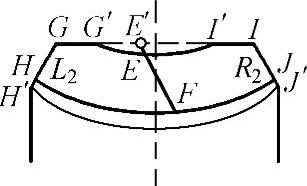
图8-4 蜗轮齿面上的边界点图

点E′不是蜗轮齿面上的边界点，但为了后续计算，需要计算该点。点E′在蜗轮齿面上瞬时接触线奇点轨迹曲线上，并且在蜗轮外圆上，所以满足式（7-62）和式（8-9）。

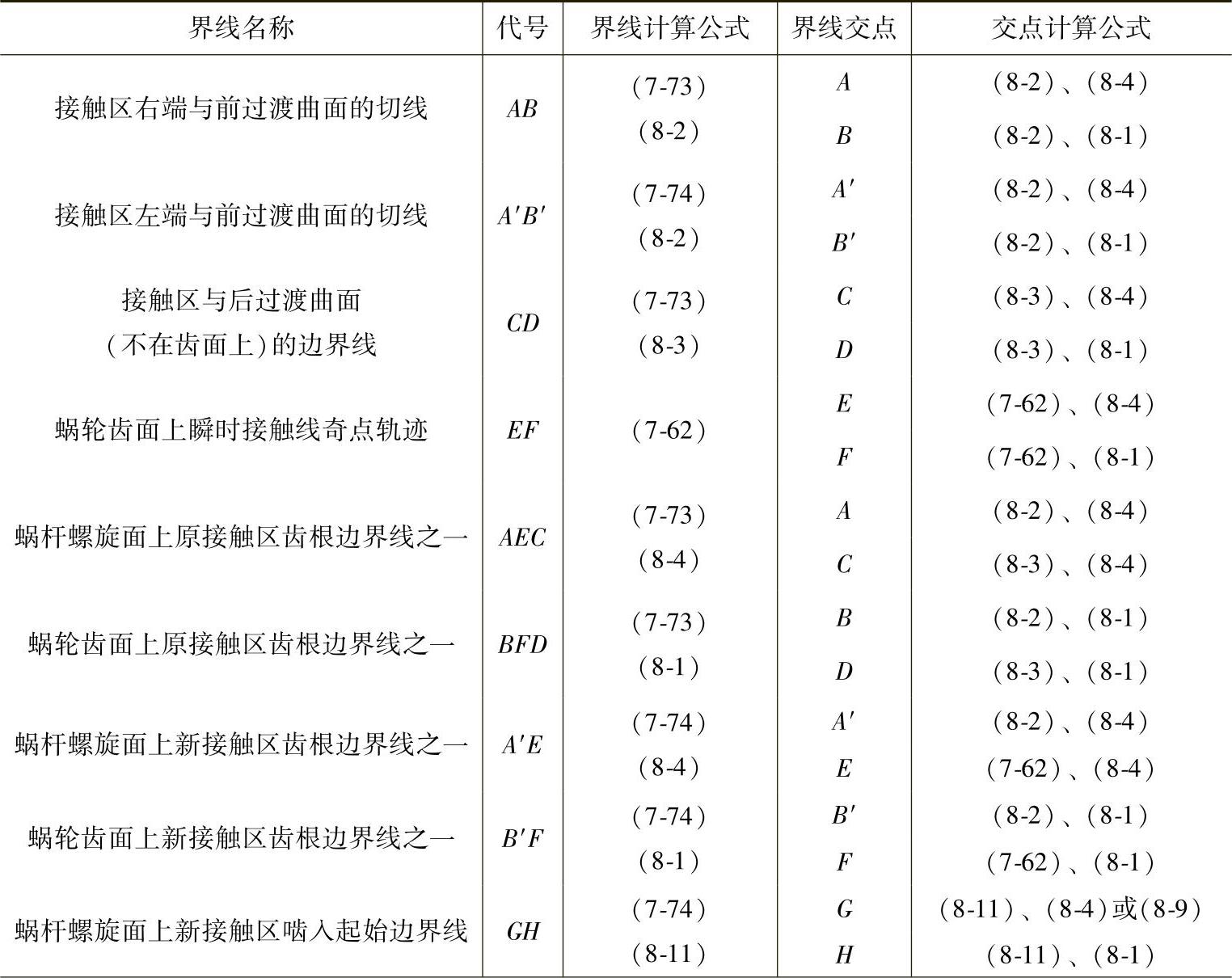
蜗杆和蜗轮齿面接触区边界线和边界点的计算公式见表8-2，但并非所有边界线都在齿面上，这取决于传动类型和设计参数：图8-5为双自由度直线标准环面蜗杆传动的接触区边界图，边界线A′B′和AB都不在蜗轮齿面上出现。

表8 - 2 双自由度直线标准环面蜗杆副接触区边界线的计算公式

（续）

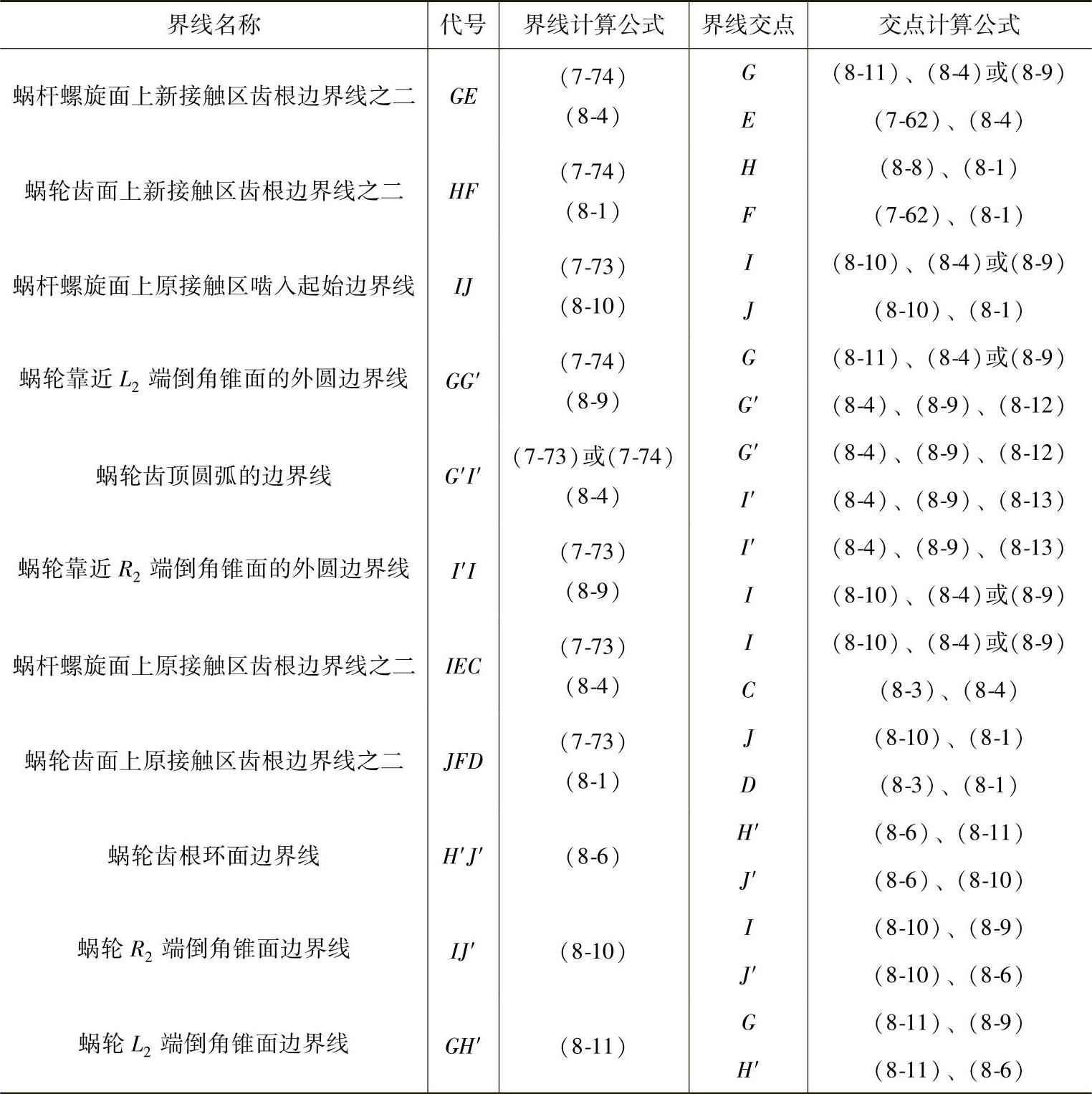
关于点I的求解，可以采用下述简单方法求解：由蜗杆切齿啮合共轭条件方程、φ=φ₁和点I在坐标系（O₂；R_B，z₀₂）里的位置可得到点I的参数（u，δ，φ=φ₁）。

因为原接触区是展成蜗杆的虚拟产形面Σ_d在蜗轮齿面上的再现，所以由蜗轮上点的z₂值可直接求出对应点的δ值为

右接触区外圆上点的u值不变，都等于蜗轮外圆与N线交点E′的u，所以计算就简单了：从E′点计算到I点，按z₂分段计算。已知u和δ，由切齿啮合共轭条件方程式（6-60）可解出φ。解法如下：

将式（6-59）整理得

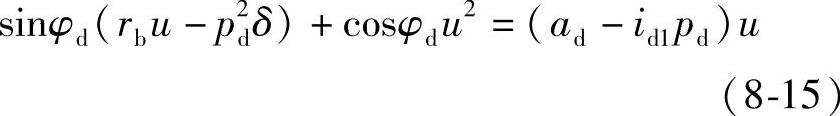
式（8-15）两边同时除以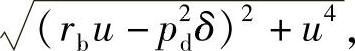得

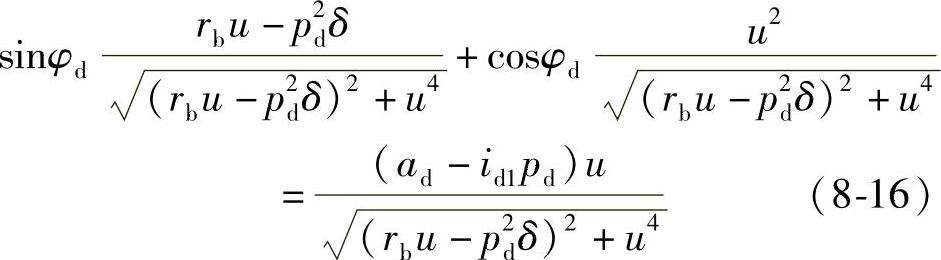
令

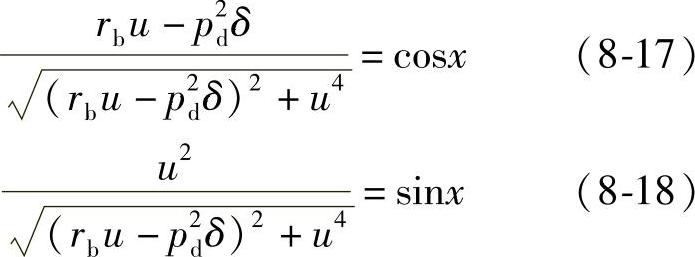
则有

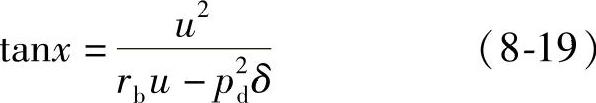
解得

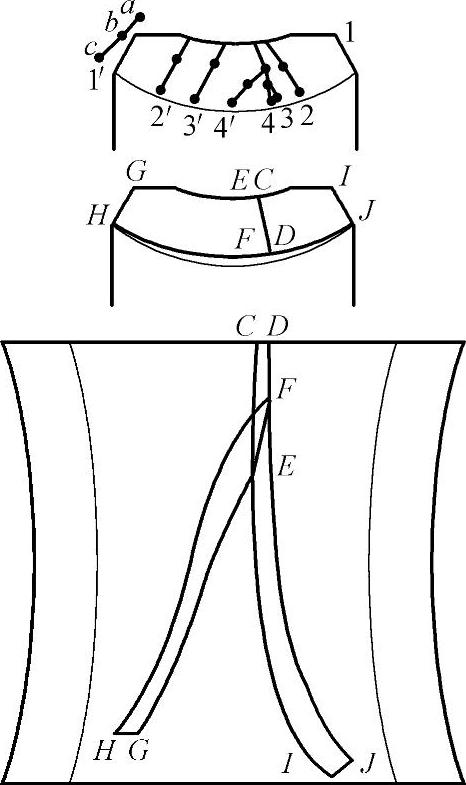
图8-5 双自由度直线环面蜗杆副的接触区边界图

将式（8-17）和式（8-18）代入式（8-16），整理得

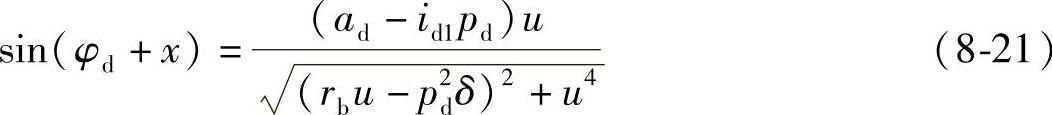
将φ_d=i_d1φ+δ代入式（8-21）得

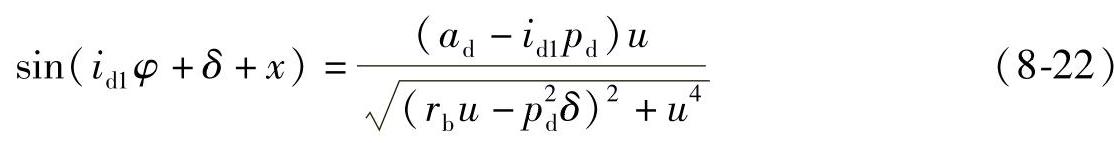
给定δ和u，由式（8-22）可解得φ。