螺旋方向与轴交角解析

通常取两角速度矢量ω₁和ω₂夹角的补角为轴交角Σ（见图5-1）。两轴平行为其特例，外啮合传动Σ=0°，内啮合传动Σ=180°；交错轴齿轮传动则0°＜Σ＜180°，Σ总为正值。

在轮1渐开螺旋面齿面Σ₁的方程式（4-8）中，规定右旋齿轮螺旋参数p₁为正，因而分度圆螺旋角β₁、节圆螺旋角β′₁和基圆螺旋角β_b1均取正值；左旋齿轮p₁和基圆螺旋角β_b1等均取负值。齿轮2的规定与此相同。需要对式（4-5）的应用，给出不同情况的通用计算公式。

如图5-1a、b所示，按角速度矢量ω₁和ω₂的回转方向，轴交角Σ≤90°。图5-1a中齿轮1置于齿轮2之下；图5-1b中齿轮1置于齿轮2之上。图5-1c和d中，保持ω₁的方向不变，改变齿轮2的回转方向，即改变ω₂方向，则Σ＞90°。图5-1c中齿轮1下置，图5-1d中齿轮1上置。

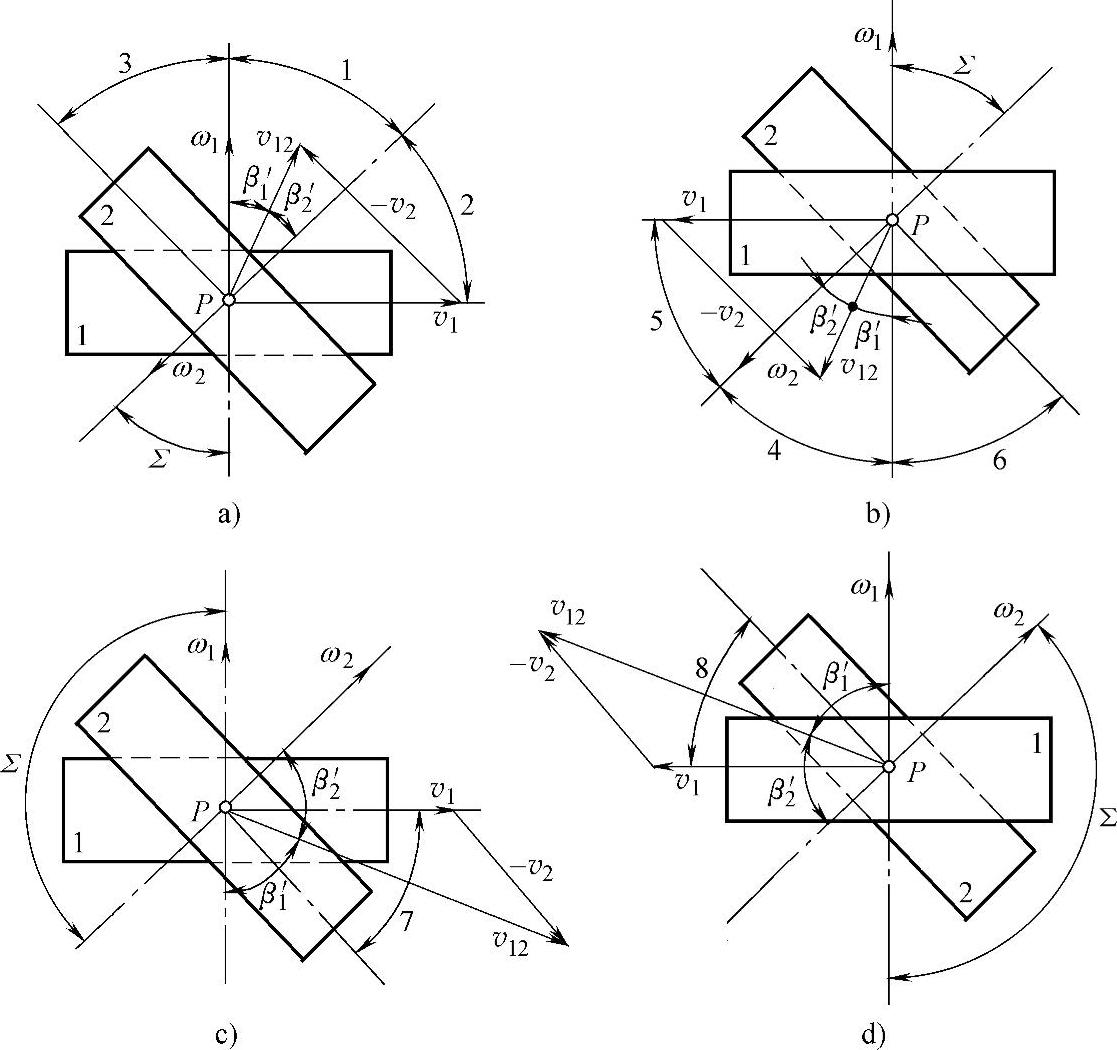
图5-1 轴交角与螺旋方向

a）Σ≤90°，齿轮1下置 b）Σ≤90°，齿轮1上置 c）Σ＞90°，齿轮1下置 d）Σ＞90°，齿轮1上置

齿线的方向应与节点P的两轮相对速度v₁₂的方向一致，因此可以根据v₁₂方向确定齿轮的螺旋方向和螺旋角的大小。在各图上过节点P，作节点P相对速度v₁₂=v₁-v₂的矢量图。

如图5-1a所示，v₁₂处于“1”区时，齿轮1和齿轮2齿的螺旋方向均为右旋。随着v₂的减小β′₁增大，β′₂减小。当β′₁＞Σ时，v₁₂处于“2”区，齿轮1右旋，齿轮2左旋。随着v₂增大，β′₁减小，β₂′增大。当β′₂＞Σ时，v₁₂处于“3”区，齿轮1左旋，齿轮2右旋。图5-1d中，v₁₂处于“8”区，在这种情况下，齿轮1和齿轮2都只能是右旋齿轮。对于图5-1a和图5-1d这两种情况，轴交角与两轮节圆螺旋角之间的关系为(www.xing528.com)

Σ=β′₁+β′₂ （5-1）

如图5-1b所示，v₁₂处于“4”区时，齿轮1和齿轮2都为左旋齿轮，当v₁₂处于“5”区时，β′₁＞Σ，齿轮1左旋，齿轮2右旋。当v₁₂处于“6”区时，β′₂＞Σ，齿轮1右旋，齿轮2左旋。图5-1c中，v₁₂处于“7”区，齿轮1和齿轮2都只能是左旋齿轮。对于图5-1b和图5-1c这两种情况，轴交角与两轮节圆螺旋角之间的关系为

Σ=-（β′₁+β′₂） （5-2）

根据式（5-1）和式（5-2），在考虑螺旋角的符号的情况下，计算轴交角的通式为

Σ=β′₁+β′₂ （5-3）

也可以用另一种方式表达式（4-5），两轮螺旋方向相同时，β′₁和β′₂均取正号，螺旋方向相反时，绝对值小者取负号。