切齿啮合直线在σ01坐标系中的位置

将式（4-8）进行σ₁→σ₀₁坐标变换，得

（r₁）₀₁=r_b1e₀₁（ε）-r_b1θ₁g₀₁（ε）+p₁μk₀₁ （4-56）

将式（4-52）和式（4-53）代入式（4-56），得到啮合线在σ₀₁里的方程为

当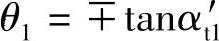时

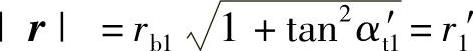
啮合线通过节点P。

将式（4-57）对θ₁求导得

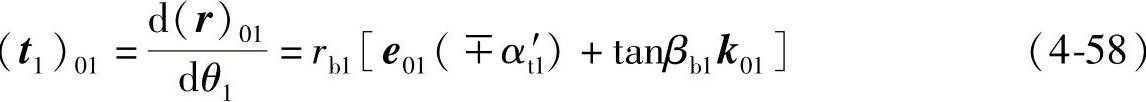
（t₁）₀₁是常矢量，啮合线是一条直线，由e₀₁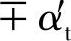（）到（t₁）₀₁的有向角λ₁=β_b1。

根据上面得到的结果，图4-4绘出啮合线相对于轮1的位置。切齿啮合线是一条直线，它通过节点P，与轮1基圆柱相切，与渐开螺旋面直母线垂直。

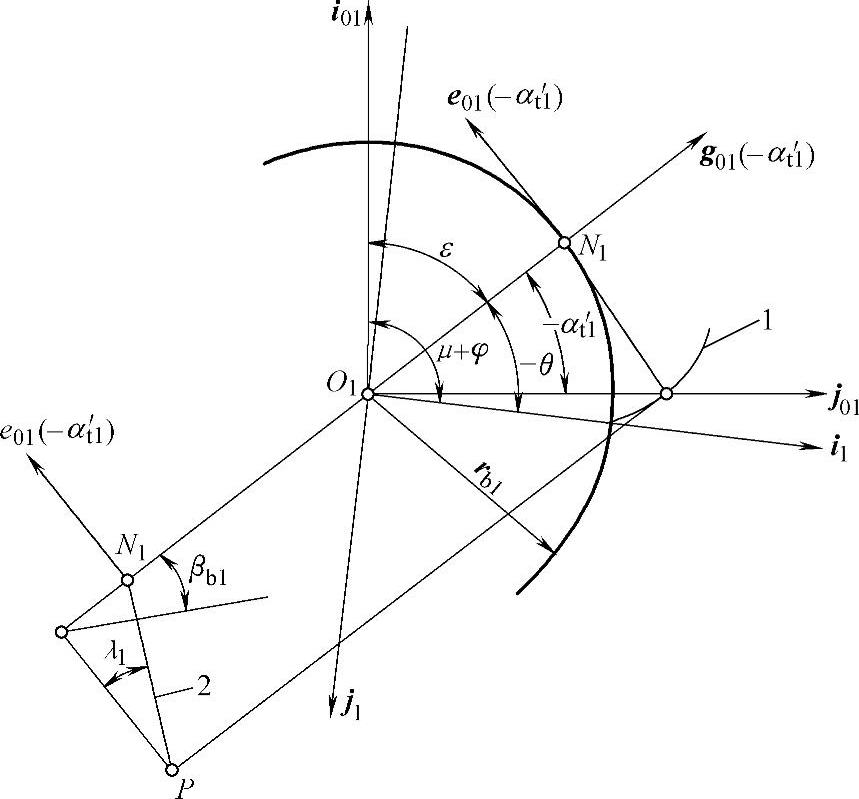
图4-4 啮合线相对于轮1的位置

1—轮1渐开线齿廓 2—切齿啮合线

将式（4-57）展开为

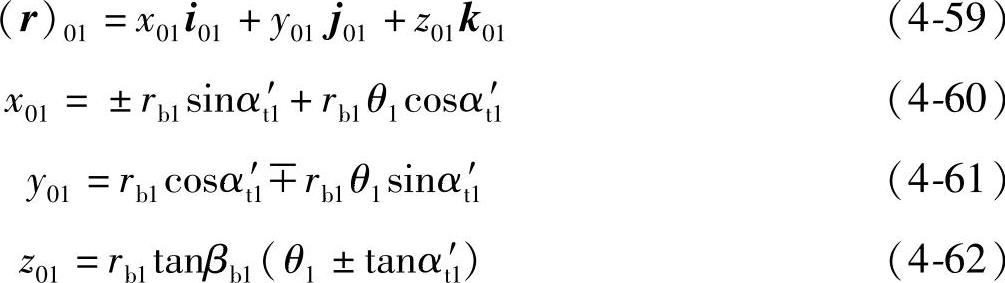
在σ₀₂里切齿啮合线的方程为

将式（4-59）代入式（4-63），并利用式（4-2）进行σ₀₁→σ₀₂坐标变换得

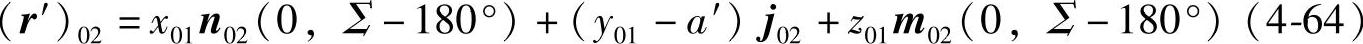
式（4-64）展开后得

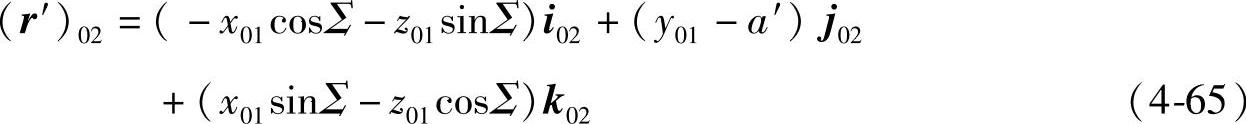
将式（4-60）～式（4-62）以及Σ=β′₁+β′₂代入式（4-65）得

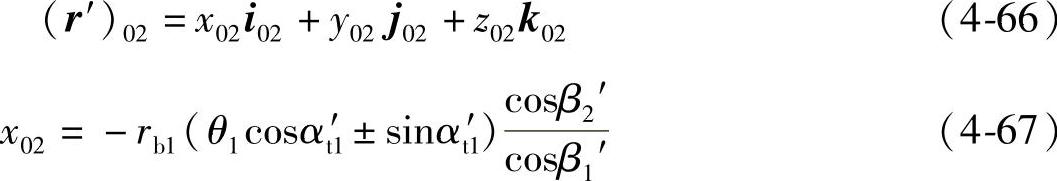
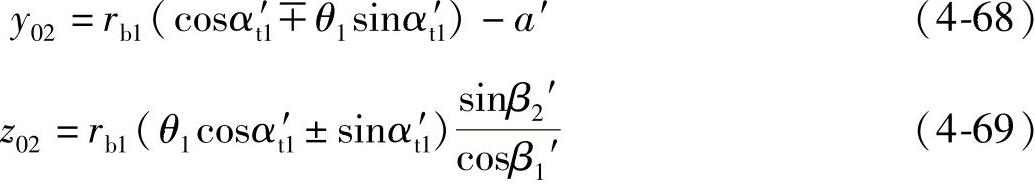
将式（4-66）对θ₁求导得

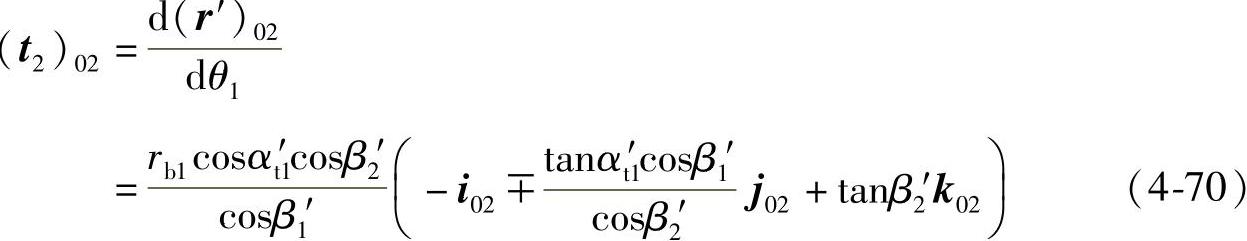
由 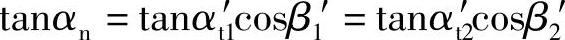(www.xing528.com)

得到

将式（4-71）代入式（4-70）得

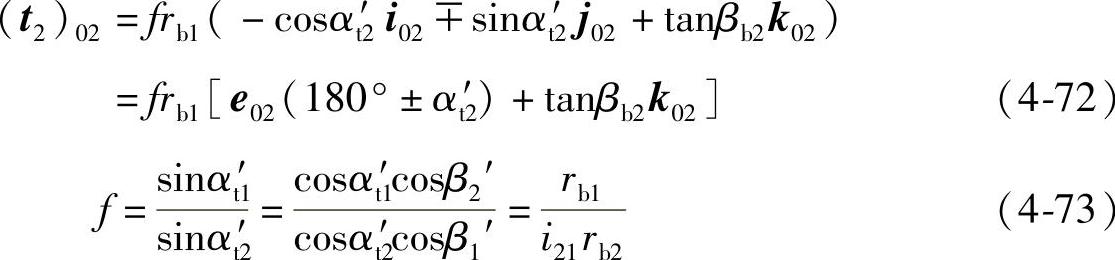
式（4-72）中双符号项，上面符号用于轮2齿的“正侧面”，下面符号用于齿的“负侧面”。

啮合线是直线，由e₀₂（180°±α′_t2）到（t）₀₂的有向角λ₂=β_b2。

式（4-66）中（r′）₀₂在垂直于k₀₂轴线的平面内的分量为

在啮合线上的垂足N₂、径矢（R′₂）₀₂应满足下面条件：

将式（4-72）和式（4-74）代入式（4-75）得

将式（4-67）和式（4-68）代入式（4-76）得

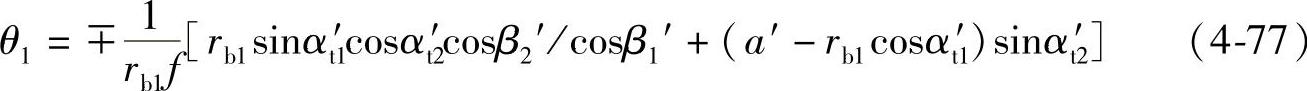
将式（4-77）代入式（4-67）得

将式（4-77）代入式（4-68）得

将式（4-78）和式（4-79）代入式（4-74）得

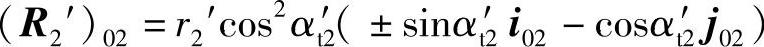
上式可以写成

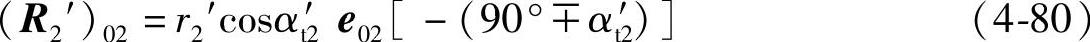
由上式可知，啮合直线与轮2轴线间公垂线的长度为

根据以上结果绘出与轮1“负侧面”相啮合的轮2“正侧面”位置示意图4-5。切齿啮合直线与半径为|R₂|=r_b2的圆柱相切。由e₀₂（180°+α′_t2）到切齿啮合线的有向角为λ₂=β_b2。

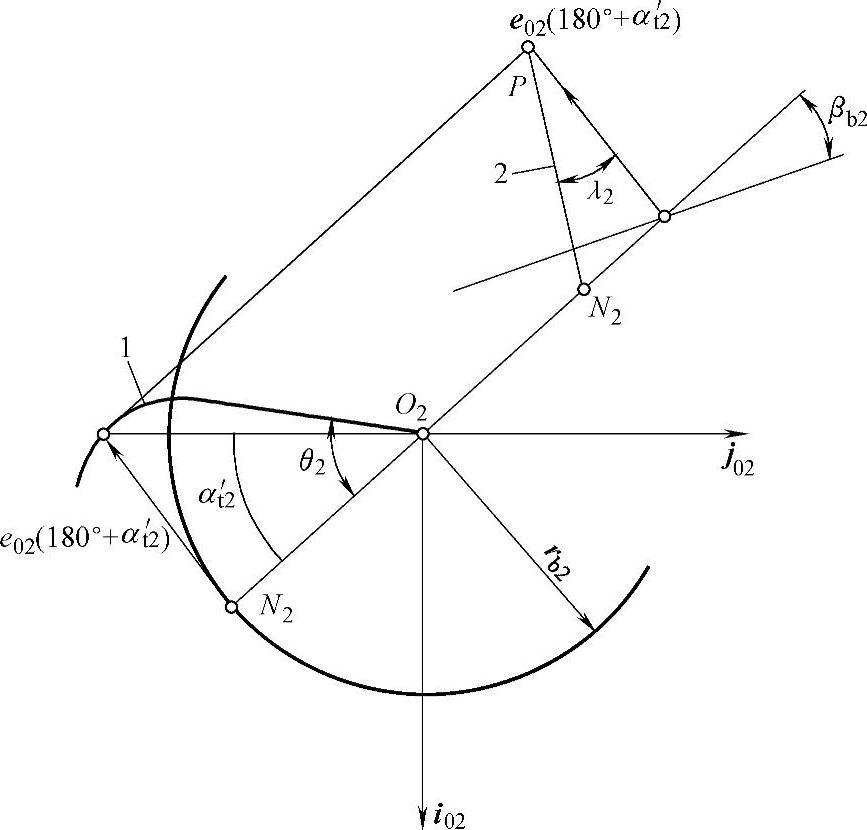
图4-5 啮合线相对于轮2的位置

1—轮2渐开线齿廓 2—切齿啮合线